GenSwarm: Scalable Multi-Robot Code-Policy Generation and Deployment via Language Models

The development of control policies for multi-robot systems traditionally follows a complex and labor-intensive process, often lacking the flexibility to adapt to dynamic tasks. This has motivated research on methods to automatically create control policies. However, these methods require iterative processes of manually crafting and refining objective functions, thereby prolonging the development cycle. This work introduces \textit{GenSwarm}, an end-to-end system that leverages large language models to automatically generate and deploy control policies for multi-robot tasks based on simple user instructions in natural language. As a multi-language-agent system, GenSwarm achieves zero-shot learning, enabling rapid adaptation to altered or unseen tasks. The white-box nature of the code policies ensures strong reproducibility and interpretability. With its scalable software and hardware architectures, GenSwarm supports efficient policy deployment on both simulated and real-world multi-robot systems, realizing an instruction-to-execution end-to-end functionality that could prove valuable for robotics specialists and non-specialists alike.The code of the proposed GenSwarm system is available online: https://github.com/WindyLab/GenSwarm.

Beyond Local Nash Equilibria for Adversarial Networks

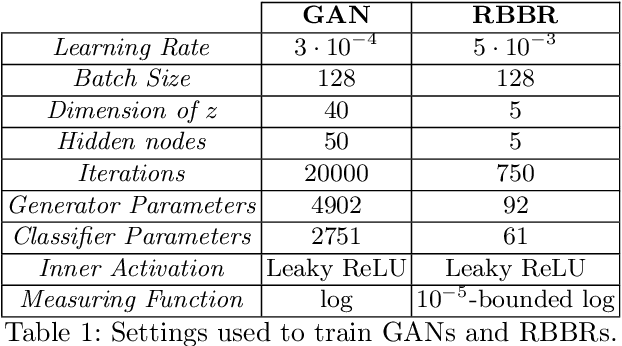
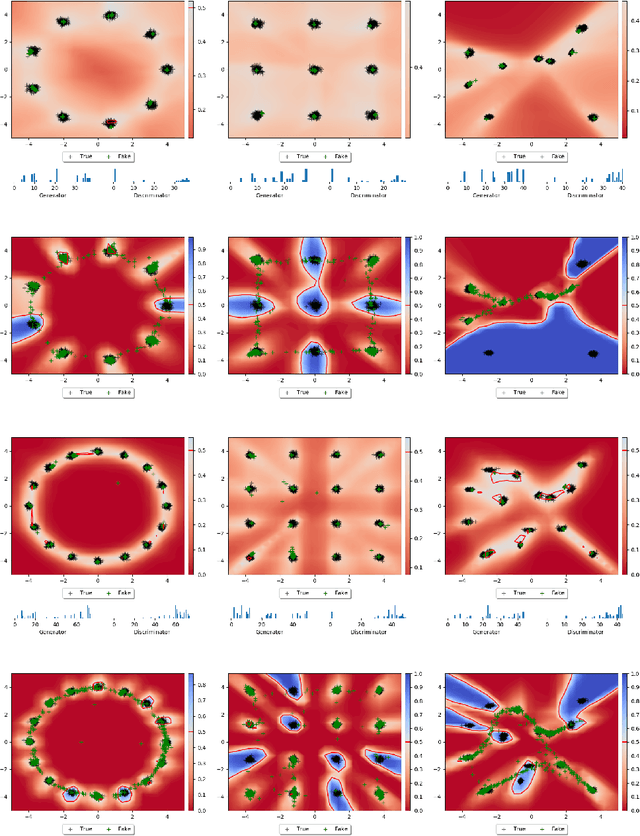
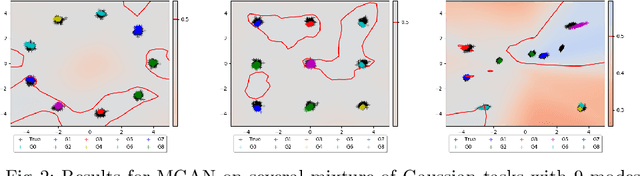
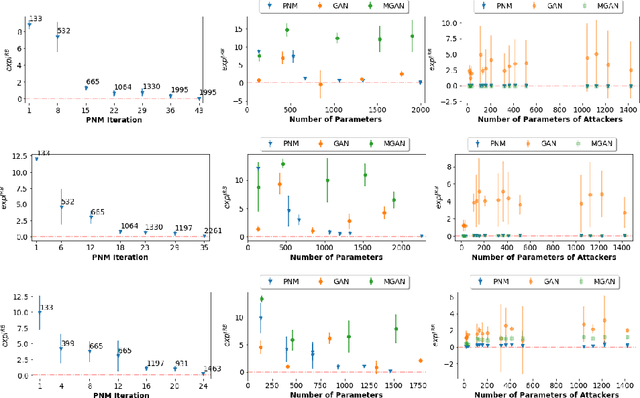
Save for some special cases, current training methods for Generative Adversarial Networks (GANs) are at best guaranteed to converge to a `local Nash equilibrium` (LNE). Such LNEs, however, can be arbitrarily far from an actual Nash equilibrium (NE), which implies that there are no guarantees on the quality of the found generator or classifier. This paper proposes to model GANs explicitly as finite games in mixed strategies, thereby ensuring that every LNE is an NE. With this formulation, we propose a solution method that is proven to monotonically converge to a resource-bounded Nash equilibrium (RB-NE): by increasing computational resources we can find better solutions. We empirically demonstrate that our method is less prone to typical GAN problems such as mode collapse, and produces solutions that are less exploitable than those produced by GANs and MGANs, and closely resemble theoretical predictions about NEs.