Iterative Methods via Locally Evolving Set Process
Paper and Code
Oct 19, 2024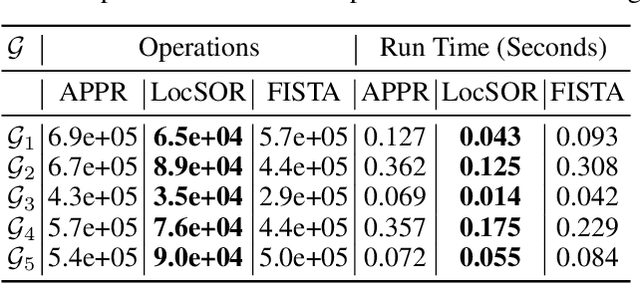
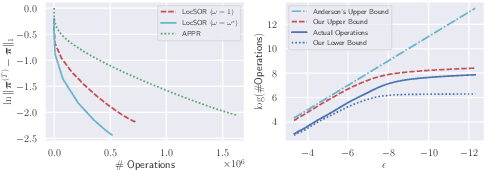


Given the damping factor $\alpha$ and precision tolerance $\epsilon$, \citet{andersen2006local} introduced Approximate Personalized PageRank (APPR), the \textit{de facto local method} for approximating the PPR vector, with runtime bounded by $\Theta(1/(\alpha\epsilon))$ independent of the graph size. Recently, \citet{fountoulakis2022open} asked whether faster local algorithms could be developed using $\tilde{O}(1/(\sqrt{\alpha}\epsilon))$ operations. By noticing that APPR is a local variant of Gauss-Seidel, this paper explores the question of \textit{whether standard iterative solvers can be effectively localized}. We propose to use the \textit{locally evolving set process}, a novel framework to characterize the algorithm locality, and demonstrate that many standard solvers can be effectively localized. Let $\overline{\operatorname{vol}}{ (S_t)}$ and $\overline{\gamma}_{t}$ be the running average of volume and the residual ratio of active nodes $\textstyle S_{t}$ during the process. We show $\overline{\operatorname{vol}}{ (S_t)}/\overline{\gamma}_{t} \leq 1/\epsilon$ and prove APPR admits a new runtime bound $\tilde{O}(\overline{\operatorname{vol}}(S_t)/(\alpha\overline{\gamma}_{t}))$ mirroring the actual performance. Furthermore, when the geometric mean of residual reduction is $\Theta(\sqrt{\alpha})$, then there exists $c \in (0,2)$ such that the local Chebyshev method has runtime $\tilde{O}(\overline{\operatorname{vol}}(S_{t})/(\sqrt{\alpha}(2-c)))$ without the monotonicity assumption. Numerical results confirm the efficiency of this novel framework and show up to a hundredfold speedup over corresponding standard solvers on real-world graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge