Approximate Frank-Wolfe Algorithms over Graph-structured Support Sets
Paper and Code
Jun 29, 2021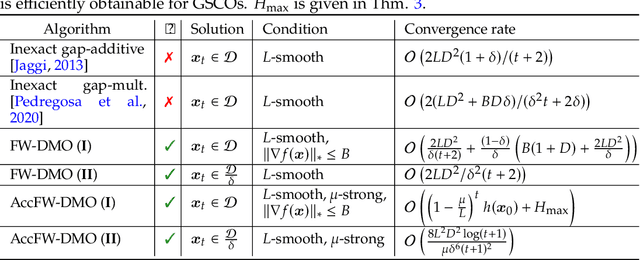
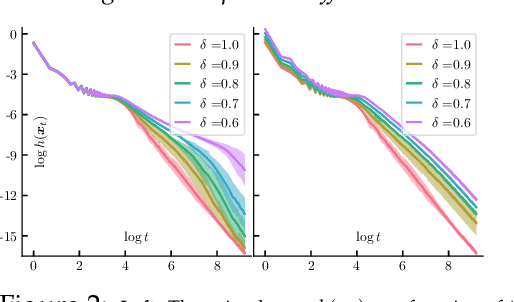
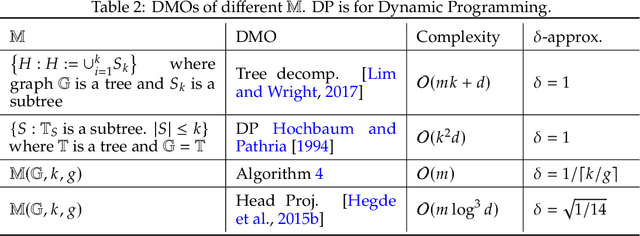
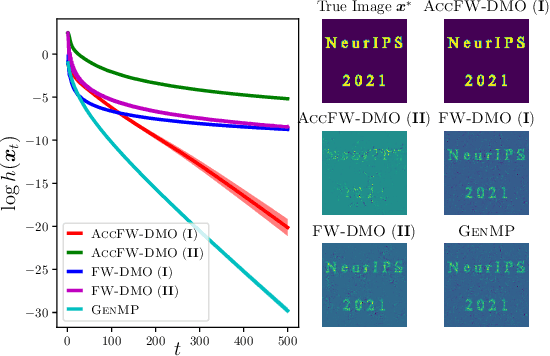
In this paper, we propose approximate Frank-Wolfe (FW) algorithms to solve convex optimization problems over graph-structured support sets where the \textit{linear minimization oracle} (LMO) cannot be efficiently obtained in general. We first demonstrate that two popular approximation assumptions (\textit{additive} and \textit{multiplicative gap errors)}, are not valid for our problem, in that no cheap gap-approximate LMO oracle exists in general. Instead, a new \textit{approximate dual maximization oracle} (DMO) is proposed, which approximates the inner product rather than the gap. When the objective is $L$-smooth, we prove that the standard FW method using a $\delta$-approximate DMO converges as $\mathcal{O}(L / \delta t + (1-\delta)(\delta^{-1} + \delta^{-2}))$ in general, and as $\mathcal{O}(L/(\delta^2(t+2)))$ over a $\delta$-relaxation of the constraint set. Additionally, when the objective is $\mu$-strongly convex and the solution is unique, a variant of FW converges to $\mathcal{O}(L^2\log(t)/(\mu \delta^6 t^2))$ with the same per-iteration complexity. Our empirical results suggest that even these improved bounds are pessimistic, with significant improvement in recovering real-world images with graph-structured sparsity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge