Second-Order Min-Max Optimization with Lazy Hessians

This paper studies second-order methods for convex-concave minimax optimization. Monteiro and Svaiter (2012) proposed a method to solve the problem with an optimal iteration complexity of $\mathcal{O}(\epsilon^{-3/2})$ to find an $\epsilon$-saddle point. However, it is unclear whether the computational complexity, $\mathcal{O}((N+ d^2) d \epsilon^{-2/3})$, can be improved. In the above, we follow Doikov et al. (2023) and assume the complexity of obtaining a first-order oracle as $N$ and the complexity of obtaining a second-order oracle as $dN$. In this paper, we show that the computation cost can be reduced by reusing Hessian across iterations. Our methods take the overall computational complexity of $ \tilde{\mathcal{O}}( (N+d^2)(d+ d^{2/3}\epsilon^{-2/3}))$, which improves those of previous methods by a factor of $d^{1/3}$. Furthermore, we generalize our method to strongly-convex-strongly-concave minimax problems and establish the complexity of $\tilde{\mathcal{O}}((N+d^2) (d + d^{2/3} \kappa^{2/3}) )$ when the condition number of the problem is $\kappa$, enjoying a similar speedup upon the state-of-the-art method. Numerical experiments on both real and synthetic datasets also verify the efficiency of our method.

Functionally Constrained Algorithm Solves Convex Simple Bilevel Problems

This paper studies simple bilevel problems, where a convex upper-level function is minimized over the optimal solutions of a convex lower-level problem. We first show the fundamental difficulty of simple bilevel problems, that the approximate optimal value of such problems is not obtainable by first-order zero-respecting algorithms. Then we follow recent works to pursue the weak approximate solutions. For this goal, we propose novel near-optimal methods for smooth and nonsmooth problems by reformulating them into functionally constrained problems.

Faster Stochastic Algorithms for Minimax Optimization under Polyak--Łojasiewicz Conditions

This paper considers stochastic first-order algorithms for minimax optimization under Polyak--{\L}ojasiewicz (PL) conditions. We propose SPIDER-GDA for solving the finite-sum problem of the form $\min_x \max_y f(x,y)\triangleq \frac{1}{n} \sum_{i=1}^n f_i(x,y)$, where the objective function $f(x,y)$ is $\mu_x$-PL in $x$ and $\mu_y$-PL in $y$; and each $f_i(x,y)$ is $L$-smooth. We prove SPIDER-GDA could find an $\epsilon$-optimal solution within ${\mathcal O}\left((n + \sqrt{n}\,\kappa_x\kappa_y^2)\log (1/\epsilon)\right)$ stochastic first-order oracle (SFO) complexity, which is better than the state-of-the-art method whose SFO upper bound is ${\mathcal O}\big((n + n^{2/3}\kappa_x\kappa_y^2)\log (1/\epsilon)\big)$, where $\kappa_x\triangleq L/\mu_x$ and $\kappa_y\triangleq L/\mu_y$. For the ill-conditioned case, we provide an accelerated algorithm to reduce the computational cost further. It achieves $\tilde{{\mathcal O}}\big((n+\sqrt{n}\,\kappa_x\kappa_y)\log^2 (1/\epsilon)\big)$ SFO upper bound when $\kappa_y \gtrsim \sqrt{n}$. Our ideas also can be applied to the more general setting that the objective function only satisfies PL condition for one variable. Numerical experiments validate the superiority of proposed methods.

Near-Optimal Fully First-Order Algorithms for Finding Stationary Points in Bilevel Optimization

Bilevel optimization has various applications such as hyper-parameter optimization and meta-learning. Designing theoretically efficient algorithms for bilevel optimization is more challenging than standard optimization because the lower-level problem defines the feasibility set implicitly via another optimization problem. One tractable case is when the lower-level problem permits strong convexity. Recent works show that second-order methods can provably converge to an $\epsilon$-first-order stationary point of the problem at a rate of $\tilde{\mathcal{O}}(\epsilon^{-2})$, yet these algorithms require a Hessian-vector product oracle. Kwon et al. (2023) resolved the problem by proposing a first-order method that can achieve the same goal at a slower rate of $\tilde{\mathcal{O}}(\epsilon^{-3})$. In this work, we provide an improved analysis demonstrating that the first-order method can also find an $\epsilon$-first-order stationary point within $\tilde {\mathcal{O}}(\epsilon^{-2})$ oracle complexity, which matches the upper bounds for second-order methods in the dependency on $\epsilon$. Our analysis further leads to simple first-order algorithms that can achieve similar near-optimal rates in finding second-order stationary points and in distributed bilevel problems.

Faster Gradient-Free Algorithms for Nonsmooth Nonconvex Stochastic Optimization

We consider the optimization problem of the form $\min_{x \in \mathbb{R}^d} f(x) \triangleq \mathbb{E}_{\xi} [F(x; \xi)]$, where the component $F(x;\xi)$ is $L$-mean-squared Lipschitz but possibly nonconvex and nonsmooth. The recently proposed gradient-free method requires at most $\mathcal{O}( L^4 d^{3/2} \epsilon^{-4} + \Delta L^3 d^{3/2} \delta^{-1} \epsilon^{-4})$ stochastic zeroth-order oracle complexity to find a $(\delta,\epsilon)$-Goldstein stationary point of objective function, where~$\Delta = f(x_0) - \inf_{x \in \mathbb{R}^d} f(x)$ and $x_0$ is the initial point of the algorithm. This paper proposes a more efficient algorithm using stochastic recursive gradient estimators, which improves the complexity to~$\mathcal{O}(L^3 d^{3/2} \epsilon^{-3}+ \Delta L^2 d^{3/2} \delta^{-1} \epsilon^{-3})$.

On Bilevel Optimization without Lower-level Strong Convexity

Theoretical properties of bilevel problems are well studied when the lower-level problem is strongly convex. In this work, we focus on bilevel optimization problems without the strong-convexity assumption. In these cases, we first show that the common local optimality measures such as KKT condition or regularization can lead to undesired consequences. Then, we aim to identify the mildest conditions that make bilevel problems tractable. We identify two classes of growth conditions on the lower-level objective that leads to continuity. Under these assumptions, we show that the local optimality of the bilevel problem can be defined via the Goldstein stationarity condition of the hyper-objective. We then propose the Inexact Gradient-Free Method (IGFM) to solve the bilevel problem, using an approximate zeroth order oracle that is of independent interest. Our non-asymptotic analysis demonstrates that the proposed method can find a $(\delta, \varepsilon)$ Goldstein stationary point for bilevel problems with a zeroth order oracle complexity that is polynomial in $d, 1/\delta$ and $1/\varepsilon$.

A Simple and Efficient Stochastic Algorithm for Decentralized Nonconvex-Strongly-Concave Minimax Optimization

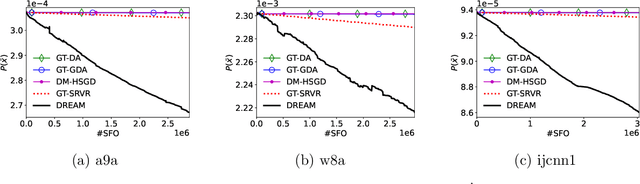
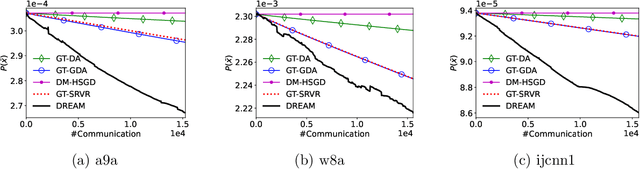
This paper studies the stochastic optimization for decentralized nonconvex-strongly-concave minimax problem. We propose a simple and efficient algorithm, called Decentralized Recursive gradient descEnt Ascent Method (DREAM), which requires $\mathcal{O}(\kappa^3\epsilon^{-3})$ stochastic first-order oracle (SFO) calls and $\mathcal{O}\big(\kappa^2\epsilon^{-2}/\sqrt{1-\lambda_2(W)}\,\big)$ communication rounds to find an $\epsilon$-stationary point, where $\kappa$ is the condition number and $\lambda_2(W)$ is the second-largest eigenvalue of the gossip matrix $W$. To the best our knowledge, DREAM is the first algorithm whose SFO and communication complexities simultaneously achieve the optimal dependency on $\epsilon$ and $\lambda_2(W)$ for this problem.

Near-Optimal Algorithms for Making the Gradient Small in Stochastic Minimax Optimization

We study the problem of finding a near-stationary point for smooth minimax optimization. The recent proposed extra anchored gradient (EAG) methods achieve the optimal convergence rate for the convex-concave minimax problem in deterministic setting. However, the direct extension of EAG to stochastic optimization is not efficient. In this paper, we design a novel stochastic algorithm called Recursive Anchored IteratioN (RAIN). We show that the RAIN achieves near-optimal stochastic first-order oracle complexity for stochastic minimax optimization in both convex-concave and strongly-convex-strongly-concave cases.