NeuralDB: Scaling Knowledge Editing in LLMs to 100,000 Facts with Neural KV Database

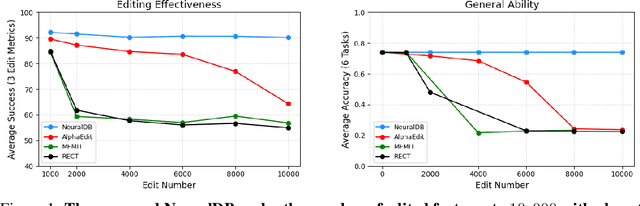
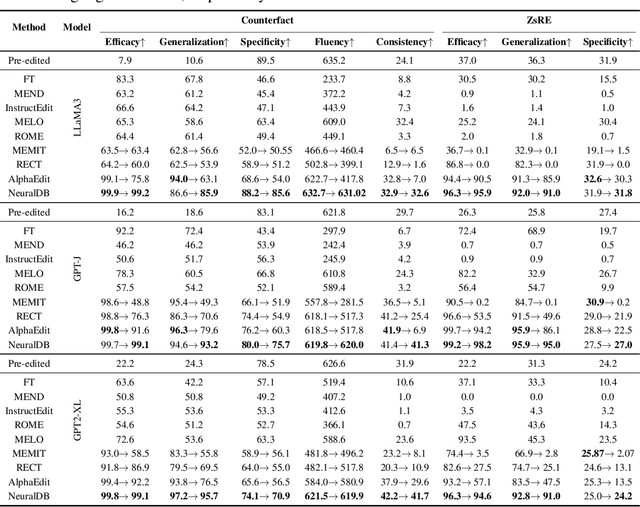
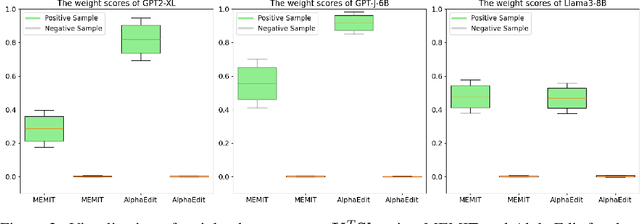
Efficiently editing knowledge stored in large language models (LLMs) enables model updates without large-scale training. One possible solution is Locate-and-Edit (L\&E), allowing simultaneous modifications of a massive number of facts. However, such editing may compromise the general abilities of LLMs and even result in forgetting edited facts when scaling up to thousands of edits. In this paper, we model existing linear L\&E methods as querying a Key-Value (KV) database. From this perspective, we then propose NeuralDB, an editing framework that explicitly represents the edited facts as a neural KV database equipped with a non-linear gated retrieval module, % In particular, our gated module only operates when inference involves the edited facts, effectively preserving the general abilities of LLMs. Comprehensive experiments involving the editing of 10,000 facts were conducted on the ZsRE and CounterFacts datasets, using GPT2-XL, GPT-J (6B) and Llama-3 (8B). The results demonstrate that NeuralDB not only excels in editing efficacy, generalization, specificity, fluency, and consistency, but also preserves overall performance across six representative text understanding and generation tasks. Further experiments indicate that NeuralDB maintains its effectiveness even when scaled to 100,000 facts (\textbf{50x} more than in prior work).

QuestA: Expanding Reasoning Capacity in LLMs via Question Augmentation

Reinforcement learning (RL) has become a key component in training large language reasoning models (LLMs). However, recent studies questions its effectiveness in improving multi-step reasoning-particularly on hard problems. To address this challenge, we propose a simple yet effective strategy via Question Augmentation: introduce partial solutions during training to reduce problem difficulty and provide more informative learning signals. Our method, QuestA, when applied during RL training on math reasoning tasks, not only improves pass@1 but also pass@k-particularly on problems where standard RL struggles to make progress. This enables continual improvement over strong open-source models such as DeepScaleR and OpenMath Nemotron, further enhancing their reasoning capabilities. We achieve new state-of-the-art results on math benchmarks using 1.5B-parameter models: 67.1% (+5.3%) on AIME24, 59.5% (+10.0%) on AIME25, and 35.5% (+4.0%) on HMMT25. Further, we provide theoretical explanations that QuestA improves sample efficiency, offering a practical and generalizable pathway for expanding reasoning capability through RL.

Solving Convex-Concave Problems with $\tilde{\mathcal{O}}(ε^{-4/7})$ Second-Order Oracle Complexity

Previous algorithms can solve convex-concave minimax problems $\min_{x \in \mathcal{X}} \max_{y \in \mathcal{Y}} f(x,y)$ with $\mathcal{O}(\epsilon^{-2/3})$ second-order oracle calls using Newton-type methods. This result has been speculated to be optimal because the upper bound is achieved by a natural generalization of the optimal first-order method. In this work, we show an improved upper bound of $\tilde{\mathcal{O}}(\epsilon^{-4/7})$ by generalizing the optimal second-order method for convex optimization to solve the convex-concave minimax problem. We further apply a similar technique to lazy Hessian algorithms and show that our proposed algorithm can also be seen as a second-order ``Catalyst'' framework (Lin et al., JMLR 2018) that could accelerate any globally convergent algorithms for solving minimax problems.

Data Mixing Can Induce Phase Transitions in Knowledge Acquisition

Large Language Models (LLMs) are typically trained on data mixtures: most data come from web scrapes, while a small portion is curated from high-quality sources with dense domain-specific knowledge. In this paper, we show that when training LLMs on such data mixtures, knowledge acquisition from knowledge-dense datasets, unlike training exclusively on knowledge-dense data (arXiv:2404.05405), does not always follow a smooth scaling law but can exhibit phase transitions with respect to the mixing ratio and model size. Through controlled experiments on a synthetic biography dataset mixed with web-scraped data, we demonstrate that: (1) as we increase the model size to a critical value, the model suddenly transitions from memorizing very few to most of the biographies; (2) below a critical mixing ratio, the model memorizes almost nothing even with extensive training, but beyond this threshold, it rapidly memorizes more biographies. We attribute these phase transitions to a capacity allocation phenomenon: a model with bounded capacity must act like a knapsack problem solver to minimize the overall test loss, and the optimal allocation across datasets can change discontinuously as the model size or mixing ratio varies. We formalize this intuition in an information-theoretic framework and reveal that these phase transitions are predictable, with the critical mixing ratio following a power-law relationship with the model size. Our findings highlight a concrete case where a good mixing recipe for large models may not be optimal for small models, and vice versa.

Understanding Nonlinear Implicit Bias via Region Counts in Input Space

One explanation for the strong generalization ability of neural networks is implicit bias. Yet, the definition and mechanism of implicit bias in non-linear contexts remains little understood. In this work, we propose to characterize implicit bias by the count of connected regions in the input space with the same predicted label. Compared with parameter-dependent metrics (e.g., norm or normalized margin), region count can be better adapted to nonlinear, overparameterized models, because it is determined by the function mapping and is invariant to reparametrization. Empirically, we found that small region counts align with geometrically simple decision boundaries and correlate well with good generalization performance. We also observe that good hyper-parameter choices such as larger learning rates and smaller batch sizes can induce small region counts. We further establish the theoretical connections and explain how larger learning rate can induce small region counts in neural networks.

Scalable Model Merging with Progressive Layer-wise Distillation

Model merging offers an effective way to integrate the capabilities of multiple fine-tuned models. However, the performance degradation of the merged model remains a challenge, particularly when none or few data are available. This paper first highlights the necessity of domain-specific data for model merging by proving that data-agnostic algorithms can have arbitrarily bad worst-case performance. Building on this theoretical insight, we explore the relationship between model merging and distillation, introducing a novel few-shot merging algorithm, ProDistill (Progressive Layer-wise Distillation). Unlike common belief that layer wise training hurts performance, we show that layer-wise teacher-student distillation not only enhances the scalability but also improves model merging performance. We conduct extensive experiments to show that compared to existing few-shot merging methods, ProDistill achieves state-of-the-art performance, with up to 6.14% and 6.61% improvements in vision and NLU tasks. Furthermore, we extend the experiments to models with over 10B parameters, showcasing the exceptional scalability of ProDistill.

Task Generalization With AutoRegressive Compositional Structure: Can Learning From $\d$ Tasks Generalize to $\d^{T}$ Tasks?

Large language models (LLMs) exhibit remarkable task generalization, solving tasks they were never explicitly trained on with only a few demonstrations. This raises a fundamental question: When can learning from a small set of tasks generalize to a large task family? In this paper, we investigate task generalization through the lens of AutoRegressive Compositional (ARC) structure, where each task is a composition of $T$ operations, and each operation is among a finite family of $\d$ subtasks. This yields a total class of size~\( \d^\TT \). We first show that generalization to all \( \d^\TT \) tasks is theoretically achievable by training on only \( \tilde{O}(\d) \) tasks. Empirically, we demonstrate that Transformers achieve such exponential task generalization on sparse parity functions via in-context learning (ICL) and Chain-of-Thought (CoT) reasoning. We further demonstrate this generalization in arithmetic and language translation, extending beyond parity functions.

Second-Order Min-Max Optimization with Lazy Hessians

This paper studies second-order methods for convex-concave minimax optimization. Monteiro and Svaiter (2012) proposed a method to solve the problem with an optimal iteration complexity of $\mathcal{O}(\epsilon^{-3/2})$ to find an $\epsilon$-saddle point. However, it is unclear whether the computational complexity, $\mathcal{O}((N+ d^2) d \epsilon^{-2/3})$, can be improved. In the above, we follow Doikov et al. (2023) and assume the complexity of obtaining a first-order oracle as $N$ and the complexity of obtaining a second-order oracle as $dN$. In this paper, we show that the computation cost can be reduced by reusing Hessian across iterations. Our methods take the overall computational complexity of $ \tilde{\mathcal{O}}( (N+d^2)(d+ d^{2/3}\epsilon^{-2/3}))$, which improves those of previous methods by a factor of $d^{1/3}$. Furthermore, we generalize our method to strongly-convex-strongly-concave minimax problems and establish the complexity of $\tilde{\mathcal{O}}((N+d^2) (d + d^{2/3} \kappa^{2/3}) )$ when the condition number of the problem is $\kappa$, enjoying a similar speedup upon the state-of-the-art method. Numerical experiments on both real and synthetic datasets also verify the efficiency of our method.

From Sparse Dependence to Sparse Attention: Unveiling How Chain-of-Thought Enhances Transformer Sample Efficiency

Chain-of-thought (CoT) significantly enhances the reasoning performance of large language models (LLM). While current theoretical studies often attribute this improvement to increased expressiveness and computational capacity, we argue that expressiveness is not the primary limitation in the LLM regime, as current large models will fail on simple tasks. Using a parity-learning setup, we demonstrate that CoT can substantially improve sample efficiency even when the representation power is sufficient. Specifically, with CoT, a transformer can learn the function within polynomial samples, whereas without CoT, the required sample size is exponential. Additionally, we show that CoT simplifies the learning process by introducing sparse sequential dependencies among input tokens, and leads to a sparse and interpretable attention. We validate our theoretical analysis with both synthetic and real-world experiments, confirming that sparsity in attention layers is a key factor of the improvement induced by CoT.

Functionally Constrained Algorithm Solves Convex Simple Bilevel Problems

This paper studies simple bilevel problems, where a convex upper-level function is minimized over the optimal solutions of a convex lower-level problem. We first show the fundamental difficulty of simple bilevel problems, that the approximate optimal value of such problems is not obtainable by first-order zero-respecting algorithms. Then we follow recent works to pursue the weak approximate solutions. For this goal, we propose novel near-optimal methods for smooth and nonsmooth problems by reformulating them into functionally constrained problems.