PaTH Attention: Position Encoding via Accumulating Householder Transformations

The attention mechanism is a core primitive in modern large language models (LLMs) and AI more broadly. Since attention by itself is permutation-invariant, position encoding is essential for modeling structured domains such as language. Rotary position encoding (RoPE) has emerged as the de facto standard approach for position encoding and is part of many modern LLMs. However, in RoPE the key/query transformation between two elements in a sequence is only a function of their relative position and otherwise independent of the actual input. This limits the expressivity of RoPE-based transformers. This paper describes PaTH, a flexible data-dependent position encoding scheme based on accumulated products of Householder(like) transformations, where each transformation is data-dependent, i.e., a function of the input. We derive an efficient parallel algorithm for training through exploiting a compact representation of products of Householder matrices, and implement a FlashAttention-style blockwise algorithm that minimizes I/O cost. Across both targeted synthetic benchmarks and moderate-scale real-world language modeling experiments, we find that PaTH demonstrates superior performance compared to RoPE and other recent baselines.

Gated Attention for Large Language Models: Non-linearity, Sparsity, and Attention-Sink-Free

Gating mechanisms have been widely utilized, from early models like LSTMs and Highway Networks to recent state space models, linear attention, and also softmax attention. Yet, existing literature rarely examines the specific effects of gating. In this work, we conduct comprehensive experiments to systematically investigate gating-augmented softmax attention variants. Specifically, we perform a comprehensive comparison over 30 variants of 15B Mixture-of-Experts (MoE) models and 1.7B dense models trained on a 3.5 trillion token dataset. Our central finding is that a simple modification-applying a head-specific sigmoid gate after the Scaled Dot-Product Attention (SDPA)-consistently improves performance. This modification also enhances training stability, tolerates larger learning rates, and improves scaling properties. By comparing various gating positions and computational variants, we attribute this effectiveness to two key factors: (1) introducing non-linearity upon the low-rank mapping in the softmax attention, and (2) applying query-dependent sparse gating scores to modulate the SDPA output. Notably, we find this sparse gating mechanism mitigates 'attention sink' and enhances long-context extrapolation performance, and we also release related $\href{https://github.com/qiuzh20/gated_attention}{codes}$ and $\href{https://huggingface.co/QwQZh/gated_attention}{models}$ to facilitate future research.

Weight Ensembling Improves Reasoning in Language Models

We investigate a failure mode that arises during the training of reasoning models, where the diversity of generations begins to collapse, leading to suboptimal test-time scaling. Notably, the Pass@1 rate reliably improves during supervised finetuning (SFT), but Pass@k rapidly deteriorates. Surprisingly, a simple intervention of interpolating the weights of the latest SFT checkpoint with an early checkpoint, otherwise known as WiSE-FT, almost completely recovers Pass@k while also improving Pass@1. The WiSE-FT variant achieves better test-time scaling (Best@k, majority vote) and achieves superior results with less data when tuned further by reinforcement learning. Finally, we find that WiSE-FT provides complementary performance gains that cannot be achieved only through diversity-inducing decoding strategies, like temperature scaling. We formalize a bias-variance tradeoff of Pass@k with respect to the expectation and variance of Pass@1 over the test distribution. We find that WiSE-FT can reduce bias and variance simultaneously, while temperature scaling inherently trades-off between bias and variance.

Overtrained Language Models Are Harder to Fine-Tune

Large language models are pre-trained on ever-growing token budgets under the assumption that better pre-training performance translates to improved downstream models. In this work, we challenge this assumption and show that extended pre-training can make models harder to fine-tune, leading to degraded final performance. We term this phenomenon catastrophic overtraining. For example, the instruction-tuned OLMo-1B model pre-trained on 3T tokens leads to over 2% worse performance on multiple standard LLM benchmarks than its 2.3T token counterpart. Through controlled experiments and theoretical analysis, we show that catastrophic overtraining arises from a systematic increase in the broad sensitivity of pre-trained parameters to modifications, including but not limited to fine-tuning. Our findings call for a critical reassessment of pre-training design that considers the downstream adaptability of the model.

Symmetrical Visual Contrastive Optimization: Aligning Vision-Language Models with Minimal Contrastive Images

Recent studies have shown that Large Vision-Language Models (VLMs) tend to neglect image content and over-rely on language-model priors, resulting in errors in visually grounded tasks and hallucinations. We hypothesize that this issue arises because existing VLMs are not explicitly trained to generate texts that are accurately grounded in fine-grained image details. To enhance visual feedback during VLM training, we propose S-VCO (Symmetrical Visual Contrastive Optimization), a novel finetuning objective that steers the model toward capturing important visual details and aligning them with corresponding text tokens. To further facilitate this detailed alignment, we introduce MVC, a paired image-text dataset built by automatically filtering and augmenting visual counterfactual data to challenge the model with hard contrastive cases involving Minimal Visual Contrasts. Experiments show that our method consistently improves VLM performance across diverse benchmarks covering various abilities and domains, achieving up to a 22% reduction in hallucinations, and significant gains in vision-centric and general tasks. Notably, these improvements become increasingly pronounced in benchmarks with higher visual dependency. In short, S-VCO offers a significant enhancement of VLM's visually-dependent task performance while retaining or even improving the model's general abilities. We opensource our code at https://s-vco.github.io/

Task Generalization With AutoRegressive Compositional Structure: Can Learning From $\d$ Tasks Generalize to $\d^{T}$ Tasks?

Large language models (LLMs) exhibit remarkable task generalization, solving tasks they were never explicitly trained on with only a few demonstrations. This raises a fundamental question: When can learning from a small set of tasks generalize to a large task family? In this paper, we investigate task generalization through the lens of AutoRegressive Compositional (ARC) structure, where each task is a composition of $T$ operations, and each operation is among a finite family of $\d$ subtasks. This yields a total class of size~\( \d^\TT \). We first show that generalization to all \( \d^\TT \) tasks is theoretically achievable by training on only \( \tilde{O}(\d) \) tasks. Empirically, we demonstrate that Transformers achieve such exponential task generalization on sparse parity functions via in-context learning (ICL) and Chain-of-Thought (CoT) reasoning. We further demonstrate this generalization in arithmetic and language translation, extending beyond parity functions.

Demons in the Detail: On Implementing Load Balancing Loss for Training Specialized Mixture-of-Expert Models

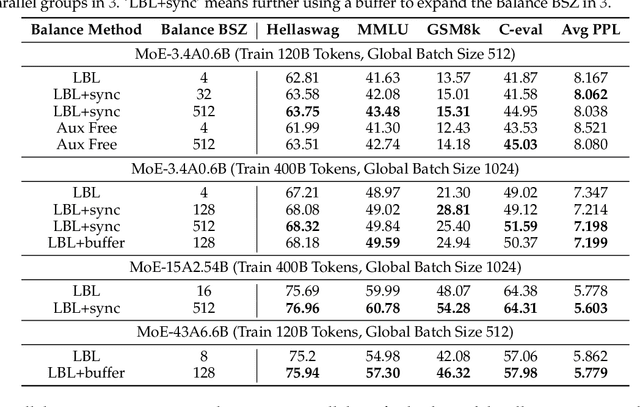
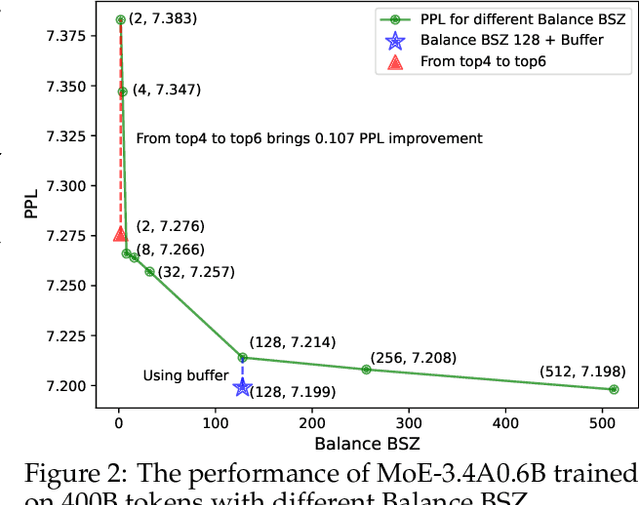
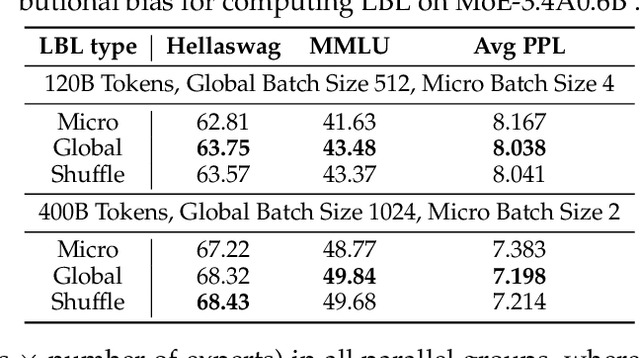
This paper revisits the implementation of $\textbf{L}$oad-$\textbf{b}$alancing $\textbf{L}$oss (LBL) when training Mixture-of-Experts (MoEs) models. Specifically, LBL for MoEs is defined as $N_E \sum_{i=1}^{N_E} f_i p_i$, where $N_E$ is the total number of experts, $f_i$ represents the frequency of expert $i$ being selected, and $p_i$ denotes the average gating score of the expert $i$. Existing MoE training frameworks usually employ the parallel training strategy so that $f_i$ and the LBL are calculated within a $\textbf{micro-batch}$ and then averaged across parallel groups. In essence, a micro-batch for training billion-scale LLMs normally contains very few sequences. So, the micro-batch LBL is almost at the sequence level, and the router is pushed to distribute the token evenly within each sequence. Under this strict constraint, even tokens from a domain-specific sequence ($\textit{e.g.}$, code) are uniformly routed to all experts, thereby inhibiting expert specialization. In this work, we propose calculating LBL using a $\textbf{global-batch}$ to loose this constraint. Because a global-batch contains much more diverse sequences than a micro-batch, which will encourage load balance at the corpus level. Specifically, we introduce an extra communication step to synchronize $f_i$ across micro-batches and then use it to calculate the LBL. Through experiments on training MoEs-based LLMs (up to $\textbf{42.8B}$ total parameters and $\textbf{400B}$ tokens), we surprisingly find that the global-batch LBL strategy yields excellent performance gains in both pre-training perplexity and downstream tasks. Our analysis reveals that the global-batch LBL also greatly improves the domain specialization of MoE experts.

Understanding Warmup-Stable-Decay Learning Rates: A River Valley Loss Landscape Perspective

Training language models currently requires pre-determining a fixed compute budget because the typical cosine learning rate schedule depends on the total number of steps. In contrast, the Warmup-Stable-Decay (WSD) schedule uses a constant learning rate to produce a main branch of iterates that can in principle continue indefinitely without a pre-specified compute budget. Then, given any compute budget, one can branch out from the main branch at a proper at any time with a rapidly decaying learning rate to produce a strong model. Empirically, WSD generates a non-traditional loss curve: the loss remains elevated during the stable phase but sharply declines during the decay phase. Towards explaining this phenomenon, we conjecture that pretraining loss exhibits a river valley landscape, which resembles a deep valley with a river at its bottom. Under this assumption, we show that during the stable phase, the iterate undergoes large oscillations due to the high learning rate, yet it progresses swiftly along the river. During the decay phase, the rapidly dropping learning rate minimizes the iterate's oscillations, moving it closer to the river and revealing true optimization progress. Therefore, the sustained high learning rate phase and fast decaying phase are responsible for progress in the river and the mountain directions respectively, and are both critical. Our analysis predicts phenomenons consistent with empirical observations and shows that this landscape can emerge from pretraining on a simple bi-gram dataset. Inspired by the theory, we introduce WSD-S, a variant of WSD that reuses previous checkpoints' decay phases and keeps only one main branch, where we resume from a decayed checkpoint. WSD-S empirically outperforms WSD and Cyclic-Cosine in obtaining multiple language model checkpoints across various compute budgets in a single run for parameters scaling from 0.1B to 1.2B.

From Sparse Dependence to Sparse Attention: Unveiling How Chain-of-Thought Enhances Transformer Sample Efficiency

Chain-of-thought (CoT) significantly enhances the reasoning performance of large language models (LLM). While current theoretical studies often attribute this improvement to increased expressiveness and computational capacity, we argue that expressiveness is not the primary limitation in the LLM regime, as current large models will fail on simple tasks. Using a parity-learning setup, we demonstrate that CoT can substantially improve sample efficiency even when the representation power is sufficient. Specifically, with CoT, a transformer can learn the function within polynomial samples, whereas without CoT, the required sample size is exponential. Additionally, we show that CoT simplifies the learning process by introducing sparse sequential dependencies among input tokens, and leads to a sparse and interpretable attention. We validate our theoretical analysis with both synthetic and real-world experiments, confirming that sparsity in attention layers is a key factor of the improvement induced by CoT.

RNNs are not Transformers : The Key Bottleneck on In-context Retrieval

This paper investigates the gap in representation powers of Recurrent Neural Networks (RNNs) and Transformers in the context of solving algorithmic problems. We focus on understanding whether RNNs, known for their memory efficiency in handling long sequences, can match the performance of Transformers, particularly when enhanced with Chain-of-Thought (CoT) prompting. Our theoretical analysis reveals that CoT improves RNNs but is insufficient to close the gap with Transformers. A key bottleneck lies in the inability of RNNs to perfectly retrieve information from the context, even with CoT: for several tasks that explicitly or implicitly require this capability, such as associative recall and determining if a graph is a tree, we prove that RNNs are not expressive enough to solve the tasks while Transformers can solve them with ease. Conversely, we prove that adopting techniques to enhance the in-context retrieval capability of RNNs, including Retrieval-Augmented Generation (RAG) and adding a single Transformer layer, can elevate RNNs to be capable of solving all polynomial-time solvable problems with CoT, hence closing the representation gap with Transformers.