Context-Parametric Inversion: Why Instruction Finetuning May Not Actually Improve Context Reliance

Large language models are instruction-finetuned to enhance their ability to follow user instructions and process the input context. However, even state-of-the-art models often struggle to follow the instruction, especially when the input context is not aligned with the model's parametric knowledge. This manifests as various failures, such as hallucinations where the responses are outdated, biased or contain unverified facts. In this work, we try to understand the underlying reason for this poor context reliance, especially after instruction tuning. We observe an intriguing phenomenon: during instruction tuning, the context reliance initially increases as expected, but then gradually decreases as instruction finetuning progresses. We call this phenomenon context-parametric inversion and observe it across multiple general purpose instruction tuning datasets like TULU, Alpaca and Ultrachat, as well as model families such as Llama, Mistral and Pythia. In a simple theoretical setup, we isolate why context-parametric inversion occurs along the gradient descent trajectory of instruction finetuning. We tie this phenomena to examples in the instruction finetuning data mixture where the input context provides information that is already present in the model's parametric knowledge. Our analysis suggests natural mitigation strategies that provide some limited gains, while also validating our theoretical insights. We hope that our work serves as a starting point in addressing this failure mode in a staple part of LLM training.

Why is SAM Robust to Label Noise?

Sharpness-Aware Minimization (SAM) is most known for achieving state-of the-art performances on natural image and language tasks. However, its most pronounced improvements (of tens of percent) is rather in the presence of label noise. Understanding SAM's label noise robustness requires a departure from characterizing the robustness of minimas lying in "flatter" regions of the loss landscape. In particular, the peak performance under label noise occurs with early stopping, far before the loss converges. We decompose SAM's robustness into two effects: one induced by changes to the logit term and the other induced by changes to the network Jacobian. The first can be observed in linear logistic regression where SAM provably up-weights the gradient contribution from clean examples. Although this explicit up-weighting is also observable in neural networks, when we intervene and modify SAM to remove this effect, surprisingly, we see no visible degradation in performance. We infer that SAM's effect in deeper networks is instead explained entirely by the effect SAM has on the network Jacobian. We theoretically derive the implicit regularization induced by this Jacobian effect in two layer linear networks. Motivated by our analysis, we see that cheaper alternatives to SAM that explicitly induce these regularization effects largely recover the benefits in deep networks trained on real-world datasets.

Predicting the Performance of Foundation Models via Agreement-on-the-Line

Estimating the out-of-distribution performance in regimes where labels are scarce is critical to safely deploy foundation models. Recently, it was shown that ensembles of neural networks observe the phenomena ``agreement-on-the-line'', which can be leveraged to reliably predict OOD performance without labels. However, in contrast to classical neural networks that are trained on in-distribution data from scratch for numerous epochs, foundation models undergo minimal finetuning from heavily pretrained weights, which may reduce the ensemble diversity needed to observe agreement-on-the-line. In our work, we demonstrate that when lightly finetuning multiple runs from a $\textit{single}$ foundation model, the choice of randomness during training (linear head initialization, data ordering, and data subsetting) can lead to drastically different levels of agreement-on-the-line in the resulting ensemble. Surprisingly, only random head initialization is able to reliably induce agreement-on-the-line in finetuned foundation models across vision and language benchmarks. Second, we demonstrate that ensembles of $\textit{multiple}$ foundation models pretrained on different datasets but finetuned on the same task can also show agreement-on-the-line. In total, by careful construction of a diverse ensemble, we can utilize agreement-on-the-line-based methods to predict the OOD performance of foundation models with high precision.

On the Joint Interaction of Models, Data, and Features

Learning features from data is one of the defining characteristics of deep learning, but our theoretical understanding of the role features play in deep learning is still rudimentary. To address this gap, we introduce a new tool, the interaction tensor, for empirically analyzing the interaction between data and model through features. With the interaction tensor, we make several key observations about how features are distributed in data and how models with different random seeds learn different features. Based on these observations, we propose a conceptual framework for feature learning. Under this framework, the expected accuracy for a single hypothesis and agreement for a pair of hypotheses can both be derived in closed-form. We demonstrate that the proposed framework can explain empirically observed phenomena, including the recently discovered Generalization Disagreement Equality (GDE) that allows for estimating the generalization error with only unlabeled data. Further, our theory also provides explicit construction of natural data distributions that break the GDE. Thus, we believe this work provides valuable new insight into our understanding of feature learning.

Agreement-on-the-Line: Predicting the Performance of Neural Networks under Distribution Shift

Recently, Miller et al. showed that a model's in-distribution (ID) accuracy has a strong linear correlation with its out-of-distribution (OOD) accuracy on several OOD benchmarks -- a phenomenon they dubbed ''accuracy-on-the-line''. While a useful tool for model selection (i.e., the model most likely to perform the best OOD is the one with highest ID accuracy), this fact does not help estimate the actual OOD performance of models without access to a labeled OOD validation set. In this paper, we show a similar but surprising phenomenon also holds for the agreement between pairs of neural network classifiers: whenever accuracy-on-the-line holds, we observe that the OOD agreement between the predictions of any two pairs of neural networks (with potentially different architectures) also observes a strong linear correlation with their ID agreement. Furthermore, we observe that the slope and bias of OOD vs ID agreement closely matches that of OOD vs ID accuracy. This phenomenon, which we call agreement-on-the-line, has important practical applications: without any labeled data, we can predict the OOD accuracy of classifiers}, since OOD agreement can be estimated with just unlabeled data. Our prediction algorithm outperforms previous methods both in shifts where agreement-on-the-line holds and, surprisingly, when accuracy is not on the line. This phenomenon also provides new insights into deep neural networks: unlike accuracy-on-the-line, agreement-on-the-line appears to only hold for neural network classifiers.

Efficient Maximal Coding Rate Reduction by Variational Forms

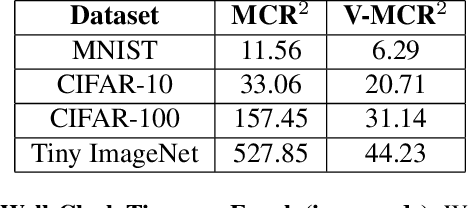
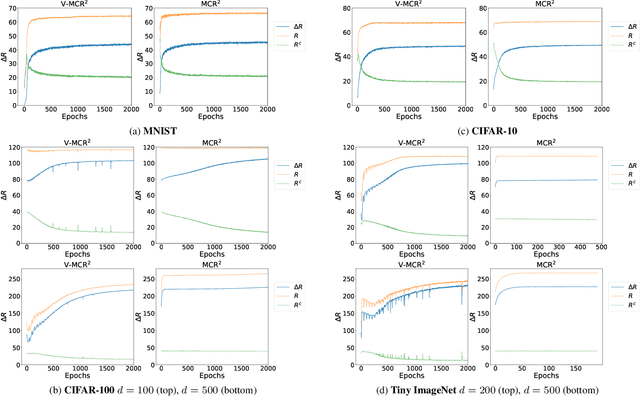
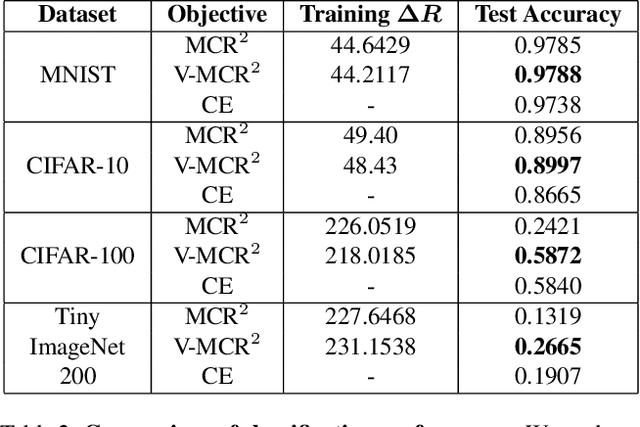
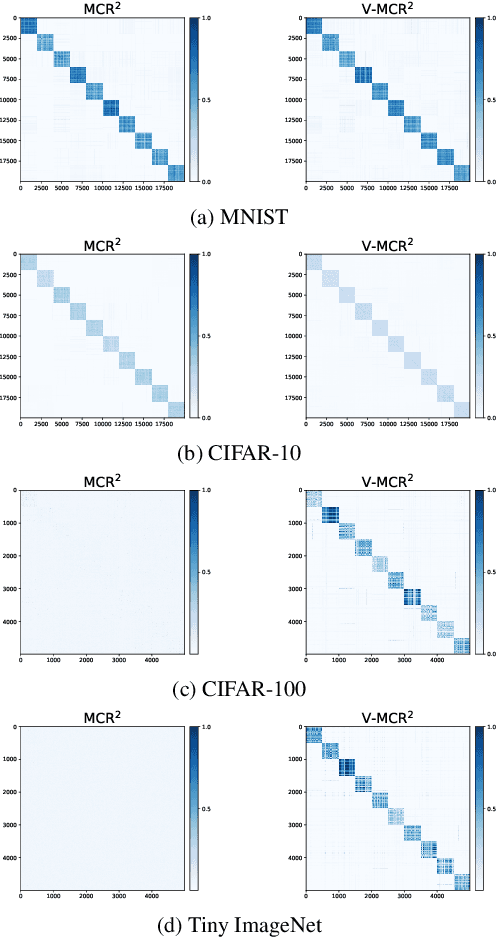
The principle of Maximal Coding Rate Reduction (MCR$^2$) has recently been proposed as a training objective for learning discriminative low-dimensional structures intrinsic to high-dimensional data to allow for more robust training than standard approaches, such as cross-entropy minimization. However, despite the advantages that have been shown for MCR$^2$ training, MCR$^2$ suffers from a significant computational cost due to the need to evaluate and differentiate a significant number of log-determinant terms that grows linearly with the number of classes. By taking advantage of variational forms of spectral functions of a matrix, we reformulate the MCR$^2$ objective to a form that can scale significantly without compromising training accuracy. Experiments in image classification demonstrate that our proposed formulation results in a significant speed up over optimizing the original MCR$^2$ objective directly and often results in higher quality learned representations. Further, our approach may be of independent interest in other models that require computation of log-determinant forms, such as in system identification or normalizing flow models.

Computational Benefits of Intermediate Rewards for Hierarchical Planning

Many hierarchical reinforcement learning (RL) applications have empirically verified that incorporating prior knowledge in reward design improves convergence speed and practical performance. We attempt to quantify the computational benefits of hierarchical RL from a planning perspective under assumptions about the intermediate state and intermediate rewards frequently (but often implicitly) adopted in practice. Our approach reveals a trade-off between computational complexity and the pursuit of the shortest path in hierarchical planning: using intermediate rewards significantly reduces the computational complexity in finding a successful policy but does not guarantee to find the shortest path, whereas using sparse terminal rewards finds the shortest path at a significantly higher computational cost. We also corroborate our theoretical results with extensive experiments on the MiniGrid environments using Q-learning and other popular deep RL algorithms.

Assessing Generalization of SGD via Disagreement

We empirically show that the test error of deep networks can be estimated by simply training the same architecture on the same training set but with a different run of Stochastic Gradient Descent (SGD), and measuring the disagreement rate between the two networks on unlabeled test data. This builds on -- and is a stronger version of -- the observation in Nakkiran & Bansal '20, which requires the second run to be on an altogether fresh training set. We further theoretically show that this peculiar phenomenon arises from the \emph{well-calibrated} nature of \emph{ensembles} of SGD-trained models. This finding not only provides a simple empirical measure to directly predict the test error using unlabeled test data, but also establishes a new conceptual connection between generalization and calibration.

Incremental Learning via Rate Reduction

Current deep learning architectures suffer from catastrophic forgetting, a failure to retain knowledge of previously learned classes when incrementally trained on new classes. The fundamental roadblock faced by deep learning methods is that deep learning models are optimized as "black boxes," making it difficult to properly adjust the model parameters to preserve knowledge about previously seen data. To overcome the problem of catastrophic forgetting, we propose utilizing an alternative "white box" architecture derived from the principle of rate reduction, where each layer of the network is explicitly computed without back propagation. Under this paradigm, we demonstrate that, given a pre-trained network and new data classes, our approach can provably construct a new network that emulates joint training with all past and new classes. Finally, our experiments show that our proposed learning algorithm observes significantly less decay in classification performance, outperforming state of the art methods on MNIST and CIFAR-10 by a large margin and justifying the use of "white box" algorithms for incremental learning even for sufficiently complex image data.