Efficient Maximal Coding Rate Reduction by Variational Forms
Paper and Code
Mar 31, 2022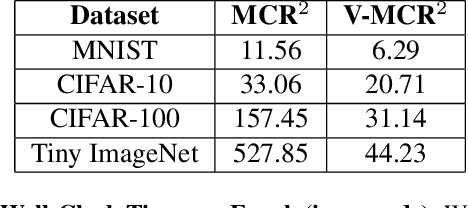
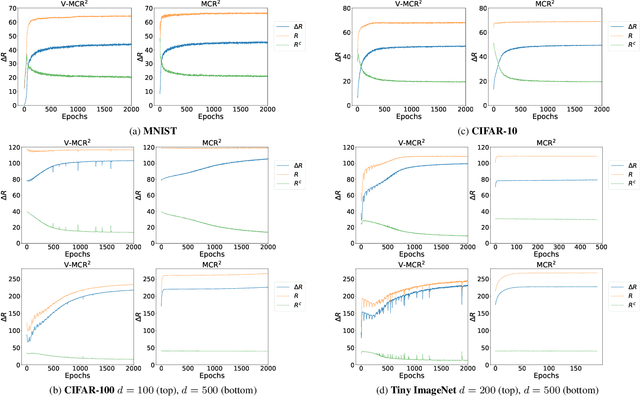
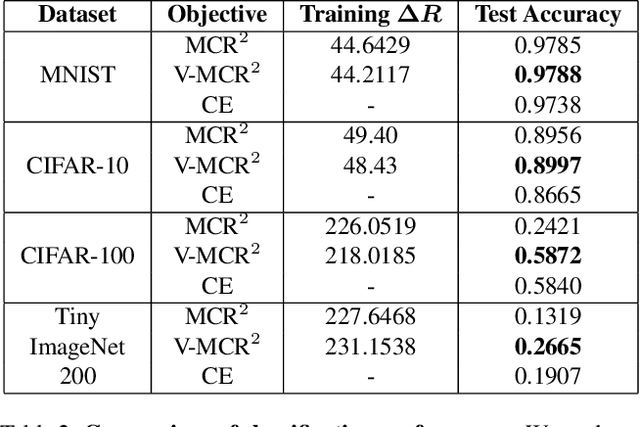
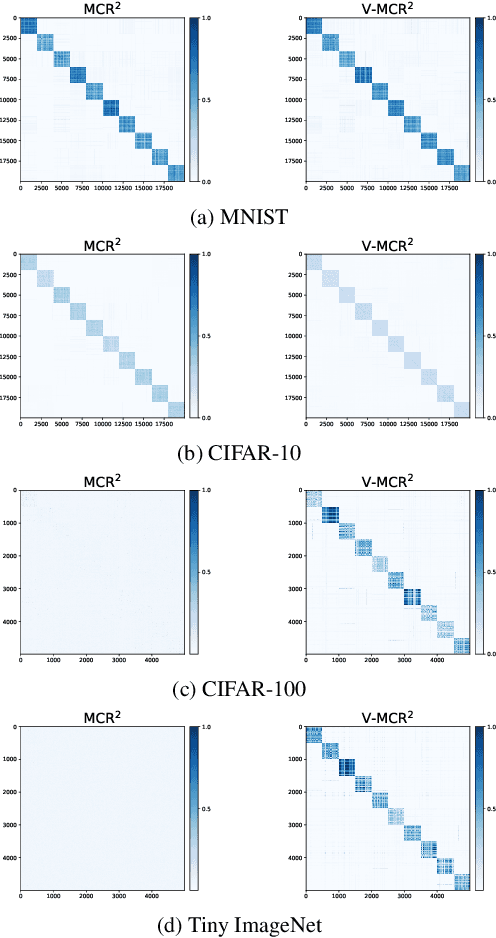
The principle of Maximal Coding Rate Reduction (MCR$^2$) has recently been proposed as a training objective for learning discriminative low-dimensional structures intrinsic to high-dimensional data to allow for more robust training than standard approaches, such as cross-entropy minimization. However, despite the advantages that have been shown for MCR$^2$ training, MCR$^2$ suffers from a significant computational cost due to the need to evaluate and differentiate a significant number of log-determinant terms that grows linearly with the number of classes. By taking advantage of variational forms of spectral functions of a matrix, we reformulate the MCR$^2$ objective to a form that can scale significantly without compromising training accuracy. Experiments in image classification demonstrate that our proposed formulation results in a significant speed up over optimizing the original MCR$^2$ objective directly and often results in higher quality learned representations. Further, our approach may be of independent interest in other models that require computation of log-determinant forms, such as in system identification or normalizing flow models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge