Vaishnavh Nagarajan
Deep sequence models tend to memorize geometrically; it is unclear why
Oct 30, 2025Abstract:In sequence modeling, the parametric memory of atomic facts has been predominantly abstracted as a brute-force lookup of co-occurrences between entities. We contrast this associative view against a geometric view of how memory is stored. We begin by isolating a clean and analyzable instance of Transformer reasoning that is incompatible with memory as strictly a storage of the local co-occurrences specified during training. Instead, the model must have somehow synthesized its own geometry of atomic facts, encoding global relationships between all entities, including non-co-occurring ones. This in turn has simplified a hard reasoning task involving an $\ell$-fold composition into an easy-to-learn 1-step geometric task. From this phenomenon, we extract fundamental aspects of neural embedding geometries that are hard to explain. We argue that the rise of such a geometry, despite optimizing over mere local associations, cannot be straightforwardly attributed to typical architectural or optimizational pressures. Counterintuitively, an elegant geometry is learned even when it is not more succinct than a brute-force lookup of associations. Then, by analyzing a connection to Node2Vec, we demonstrate how the geometry stems from a spectral bias that -- in contrast to prevailing theories -- indeed arises naturally despite the lack of various pressures. This analysis also points to practitioners a visible headroom to make Transformer memory more strongly geometric. We hope the geometric view of parametric memory encourages revisiting the default intuitions that guide researchers in areas like knowledge acquisition, capacity, discovery and unlearning.
Roll the dice & look before you leap: Going beyond the creative limits of next-token prediction
Apr 21, 2025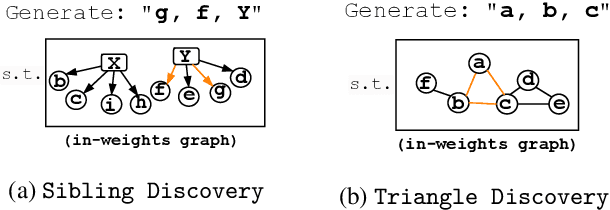
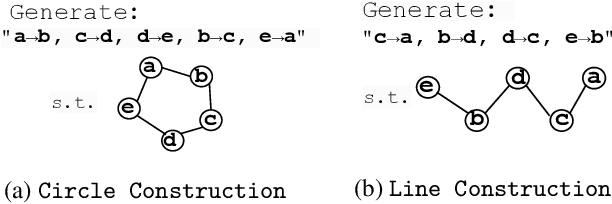
Abstract:We design a suite of minimal algorithmic tasks that are a loose abstraction of open-ended real-world tasks. This allows us to cleanly and controllably quantify the creative limits of the present-day language model. Much like real-world tasks that require a creative, far-sighted leap of thought, our tasks require an implicit, open-ended stochastic planning step that either (a) discovers new connections in an abstract knowledge graph (like in wordplay, drawing analogies, or research) or (b) constructs new patterns (like in designing math problems or new proteins). In these tasks, we empirically and conceptually argue how next-token learning is myopic and memorizes excessively; comparatively, multi-token approaches, namely teacherless training and diffusion models, excel in producing diverse and original output. Secondly, in our tasks, we find that to elicit randomness from the Transformer without hurting coherence, it is better to inject noise right at the input layer (via a method we dub hash-conditioning) rather than defer to temperature sampling from the output layer. Thus, our work offers a principled, minimal test-bed for analyzing open-ended creative skills, and offers new arguments for going beyond next-token learning and softmax-based sampling. We make part of the code available under https://github.com/chenwu98/algorithmic-creativity
Sharpness-Aware Minimization Enhances Feature Quality via Balanced Learning
May 30, 2024
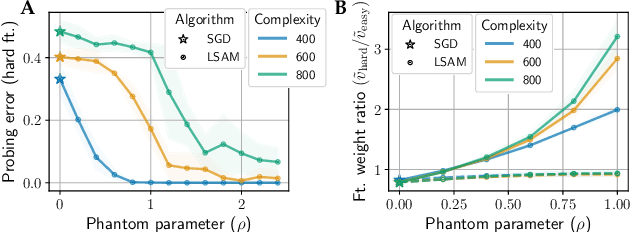
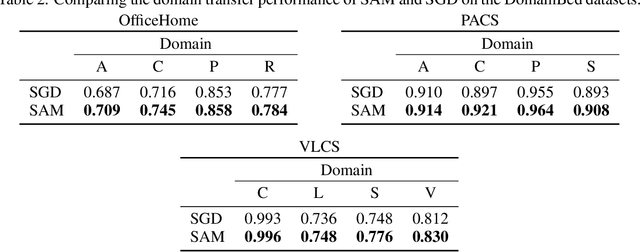
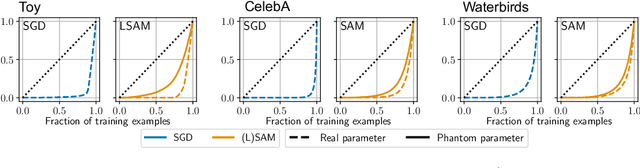
Abstract:Sharpness-Aware Minimization (SAM) has emerged as a promising alternative optimizer to stochastic gradient descent (SGD). The originally-proposed motivation behind SAM was to bias neural networks towards flatter minima that are believed to generalize better. However, recent studies have shown conflicting evidence on the relationship between flatness and generalization, suggesting that flatness does fully explain SAM's success. Sidestepping this debate, we identify an orthogonal effect of SAM that is beneficial out-of-distribution: we argue that SAM implicitly balances the quality of diverse features. SAM achieves this effect by adaptively suppressing well-learned features which gives remaining features opportunity to be learned. We show that this mechanism is beneficial in datasets that contain redundant or spurious features where SGD falls for the simplicity bias and would not otherwise learn all available features. Our insights are supported by experiments on real data: we demonstrate that SAM improves the quality of features in datasets containing redundant or spurious features, including CelebA, Waterbirds, CIFAR-MNIST, and DomainBed.
The pitfalls of next-token prediction
Mar 11, 2024Abstract:Can a mere next-token predictor faithfully model human intelligence? We crystallize this intuitive concern, which is fragmented in the literature. As a starting point, we argue that the two often-conflated phases of next-token prediction -- autoregressive inference and teacher-forced training -- must be treated distinctly. The popular criticism that errors can compound during autoregressive inference, crucially assumes that teacher-forcing has learned an accurate next-token predictor. This assumption sidesteps a more deep-rooted problem we expose: in certain classes of tasks, teacher-forcing can simply fail to learn an accurate next-token predictor in the first place. We describe a general mechanism of how teacher-forcing can fail, and design a minimal planning task where both the Transformer and the Mamba architecture empirically fail in that manner -- remarkably, despite the task being straightforward to learn. We provide preliminary evidence that this failure can be resolved when training to predict multiple tokens in advance. We hope this finding can ground future debates and inspire explorations beyond the next-token prediction paradigm. We make our code available under https://github.com/gregorbachmann/Next-Token-Failures
What do larger image classifiers memorise?
Oct 09, 2023Abstract:The success of modern neural networks has prompted study of the connection between memorisation and generalisation: overparameterised models generalise well, despite being able to perfectly fit (memorise) completely random labels. To carefully study this issue, Feldman proposed a metric to quantify the degree of memorisation of individual training examples, and empirically computed the corresponding memorisation profile of a ResNet on image classification bench-marks. While an exciting first glimpse into what real-world models memorise, this leaves open a fundamental question: do larger neural models memorise more? We present a comprehensive empirical analysis of this question on image classification benchmarks. We find that training examples exhibit an unexpectedly diverse set of memorisation trajectories across model sizes: most samples experience decreased memorisation under larger models, while the rest exhibit cap-shaped or increasing memorisation. We show that various proxies for the Feldman memorization score fail to capture these fundamental trends. Lastly, we find that knowledge distillation, an effective and popular model compression technique, tends to inhibit memorisation, while also improving generalisation. Specifically, memorisation is mostly inhibited on examples with increasing memorisation trajectories, thus pointing at how distillation improves generalisation.
The Cost of Down-Scaling Language Models: Fact Recall Deteriorates before In-Context Learning
Oct 07, 2023



Abstract:How does scaling the number of parameters in large language models (LLMs) affect their core capabilities? We study two natural scaling techniques -- weight pruning and simply training a smaller or larger model, which we refer to as dense scaling -- and their effects on two core capabilities of LLMs: (a) recalling facts presented during pre-training and (b) processing information presented in-context during inference. By curating a suite of tasks that help disentangle these two capabilities, we find a striking difference in how these two abilities evolve due to scaling. Reducing the model size by more than 30\% (via either scaling approach) significantly decreases the ability to recall facts seen in pre-training. Yet, a 60--70\% reduction largely preserves the various ways the model can process in-context information, ranging from retrieving answers from a long context to learning parameterized functions from in-context exemplars. The fact that both dense scaling and weight pruning exhibit this behavior suggests that scaling model size has an inherently disparate effect on fact recall and in-context learning.
Think before you speak: Training Language Models With Pause Tokens
Oct 03, 2023



Abstract:Language models generate responses by producing a series of tokens in immediate succession: the $(K+1)^{th}$ token is an outcome of manipulating $K$ hidden vectors per layer, one vector per preceding token. What if instead we were to let the model manipulate say, $K+10$ hidden vectors, before it outputs the $(K+1)^{th}$ token? We operationalize this idea by performing training and inference on language models with a (learnable) $\textit{pause}$ token, a sequence of which is appended to the input prefix. We then delay extracting the model's outputs until the last pause token is seen, thereby allowing the model to process extra computation before committing to an answer. We empirically evaluate $\textit{pause-training}$ on decoder-only models of 1B and 130M parameters with causal pretraining on C4, and on downstream tasks covering reasoning, question-answering, general understanding and fact recall. Our main finding is that inference-time delays show gains when the model is both pre-trained and finetuned with delays. For the 1B model, we witness gains on 8 of 9 tasks, most prominently, a gain of $18\%$ EM score on the QA task of SQuAD, $8\%$ on CommonSenseQA and $1\%$ accuracy on the reasoning task of GSM8k. Our work raises a range of conceptual and practical future research questions on making delayed next-token prediction a widely applicable new paradigm.
ResMem: Learn what you can and memorize the rest
Feb 03, 2023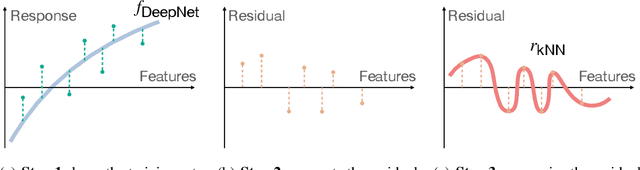

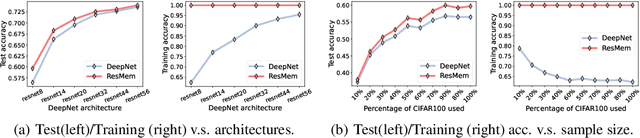
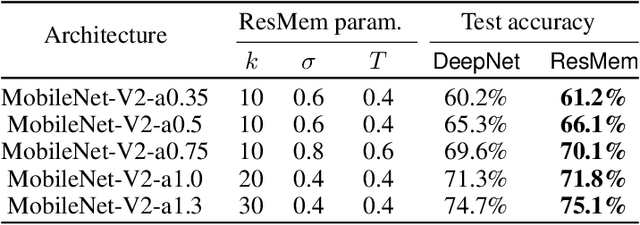
Abstract:The impressive generalization performance of modern neural networks is attributed in part to their ability to implicitly memorize complex training patterns. Inspired by this, we explore a novel mechanism to improve model generalization via explicit memorization. Specifically, we propose the residual-memorization (ResMem) algorithm, a new method that augments an existing prediction model (e.g. a neural network) by fitting the model's residuals with a $k$-nearest neighbor based regressor. The final prediction is then the sum of the original model and the fitted residual regressor. By construction, ResMem can explicitly memorize the training labels. Empirically, we show that ResMem consistently improves the test set generalization of the original prediction model across various standard vision and natural language processing benchmarks. Theoretically, we formulate a stylized linear regression problem and rigorously show that ResMem results in a more favorable test risk over the base predictor.
On student-teacher deviations in distillation: does it pay to disobey?
Jan 30, 2023



Abstract:Knowledge distillation has been widely-used to improve the performance of a "student" network by hoping to mimic soft probabilities of a "teacher" network. Yet, for self-distillation to work, the student must somehow deviate from the teacher (Stanton et al., 2021). But what is the nature of these deviations, and how do they relate to gains in generalization? We investigate these questions through a series of experiments across image and language classification datasets. First, we observe that distillation consistently deviates in a characteristic way: on points where the teacher has low confidence, the student achieves even lower confidence than the teacher. Secondly, we find that deviations in the initial dynamics of training are not crucial -- simply switching to distillation loss in the middle of training can recover much of its gains. We then provide two parallel theoretical perspectives to understand the role of student-teacher deviations in our experiments, one casting distillation as a regularizer in eigenspace, and another as a gradient denoiser. Our analysis bridges several gaps between existing theory and practice by (a) focusing on gradient-descent training, (b) by avoiding label noise assumptions, and (c) by unifying several disjoint empirical and theoretical findings.
Explaining generalization in deep learning: progress and fundamental limits
Oct 17, 2021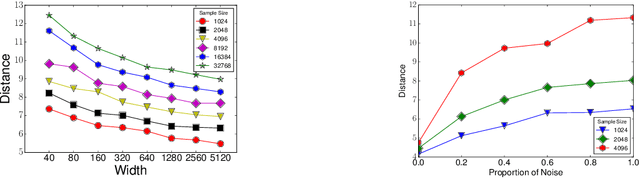



Abstract:This dissertation studies a fundamental open challenge in deep learning theory: why do deep networks generalize well even while being overparameterized, unregularized and fitting the training data to zero error? In the first part of the thesis, we will empirically study how training deep networks via stochastic gradient descent implicitly controls the networks' capacity. Subsequently, to show how this leads to better generalization, we will derive {\em data-dependent} {\em uniform-convergence-based} generalization bounds with improved dependencies on the parameter count. Uniform convergence has in fact been the most widely used tool in deep learning literature, thanks to its simplicity and generality. Given its popularity, in this thesis, we will also take a step back to identify the fundamental limits of uniform convergence as a tool to explain generalization. In particular, we will show that in some example overparameterized settings, {\em any} uniform convergence bound will provide only a vacuous generalization bound. With this realization in mind, in the last part of the thesis, we will change course and introduce an {\em empirical} technique to estimate generalization using unlabeled data. Our technique does not rely on any notion of uniform-convergece-based complexity and is remarkably precise. We will theoretically show why our technique enjoys such precision. We will conclude by discussing how future work could explore novel ways to incorporate distributional assumptions in generalization bounds (such as in the form of unlabeled data) and explore other tools to derive bounds, perhaps by modifying uniform convergence or by developing completely new tools altogether.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge