A Simple and Efficient Stochastic Algorithm for Decentralized Nonconvex-Strongly-Concave Minimax Optimization
Paper and Code
Dec 05, 2022
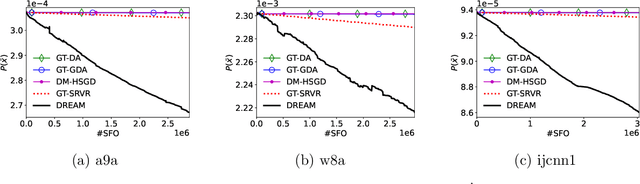
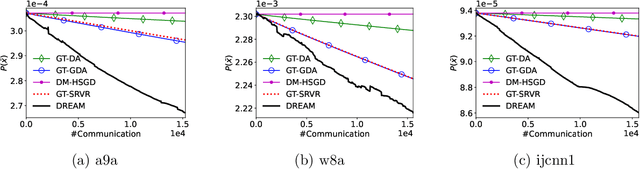
This paper studies the stochastic optimization for decentralized nonconvex-strongly-concave minimax problem. We propose a simple and efficient algorithm, called Decentralized Recursive gradient descEnt Ascent Method (DREAM), which requires $\mathcal{O}(\kappa^3\epsilon^{-3})$ stochastic first-order oracle (SFO) calls and $\mathcal{O}\big(\kappa^2\epsilon^{-2}/\sqrt{1-\lambda_2(W)}\,\big)$ communication rounds to find an $\epsilon$-stationary point, where $\kappa$ is the condition number and $\lambda_2(W)$ is the second-largest eigenvalue of the gossip matrix $W$. To the best our knowledge, DREAM is the first algorithm whose SFO and communication complexities simultaneously achieve the optimal dependency on $\epsilon$ and $\lambda_2(W)$ for this problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge