ESSAM: A Novel Competitive Evolution Strategies Approach to Reinforcement Learning for Memory Efficient LLMs Fine-Tuning

Reinforcement learning (RL) has become a key training step for improving mathematical reasoning in large language models (LLMs), but it often has high GPU memory usage, which makes it hard to use in settings with limited resources. To reduce these issues, we propose Evolution Strategies with Sharpness-Aware Maximization (ESSAM), a full parameter fine-tuning framework that tightly combines the zero-order search in parameter space from Evolution Strategies (ES) with the Sharpness-Aware Maximization (SAM) to improve generalization. We conduct fine-tuning experiments on the mainstream mathematica reasoning task GSM8K. The results show that ESSAM achieves an average accuracy of 78.27\% across all models and its overall performance is comparable to RL methods. It surpasses classic RL algorithm PPO with an accuracy of 77.72\% and is comparable to GRPO with an accuracy of 78.34\%, and even surpassing them on some models. In terms of GPU memory usage, ESSAM reduces the average GPU memory usage by $18\times$ compared to PPO and by $10\times$ compared to GRPO, achieving an extremely low GPU memory usage.

Explicit and Non-asymptotic Query Complexities of Rank-Based Zeroth-order Algorithm on Stochastic Smooth Functions

Zeroth-order (ZO) optimization with ordinal feedback has emerged as a fundamental problem in modern machine learning systems, particularly in human-in-the-loop settings such as reinforcement learning from human feedback, preference learning, and evolutionary strategies. While rank-based ZO algorithms enjoy strong empirical success and robustness properties, their theoretical understanding, especially under stochastic objectives and standard smoothness assumptions, remains limited. In this paper, we study rank-based zeroth-order optimization for stochastic functions where only ordinal feedback of the stochastic function is available. We propose a simple and computationally efficient rank-based ZO algorithm. Under standard assumptions including smoothness, strong convexity, and bounded second moments of stochastic gradients, we establish explicit non-asymptotic query complexity bounds for both convex and nonconvex objectives. Notably, our results match the best-known query complexities of value-based ZO algorithms, demonstrating that ordinal information alone is sufficient for optimal query efficiency in stochastic settings. Our analysis departs from existing drift-based and information-geometric techniques, offering new tools for the study of rank-based optimization under noise. These findings narrow the gap between theory and practice and provide a principled foundation for optimization driven by human preferences.

Numerical Sensitivity and Robustness: Exploring the Flaws of Mathematical Reasoning in Large Language Models

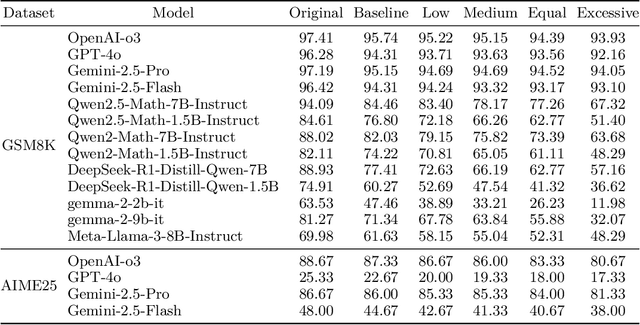
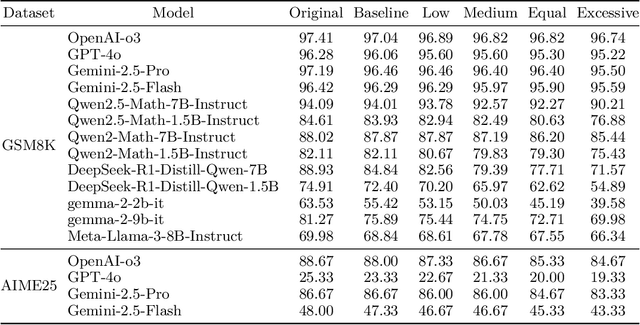
LLMs have made significant progress in the field of mathematical reasoning, but whether they have true the mathematical understanding ability is still controversial. To explore this issue, we propose a new perturbation framework to evaluate LLMs' reasoning ability in complex environments by injecting additional semantically irrelevant perturbation sentences and gradually increasing the perturbation intensity. At the same time, we use an additional perturbation method: core questioning instruction missing, to further analyze the LLMs' problem-solving mechanism. The experimental results show that LLMs perform stably when facing perturbation sentences without numbers, but there is also a robustness boundary. As the perturbation intensity increases, the performance exhibits varying degrees of decline; when facing perturbation sentences with numbers, the performance decreases more significantly, most open source models with smaller parameters decrease by nearly or even more than 10%, and further increasing with the enhancement of perturbation intensity, with the maximum decrease reaching 51.55%. Even the most advanced commercial LLMs have seen a 3%-10% performance drop. By analyzing the reasoning process of LLMs in detail, We find that models are more sensitive to perturbations with numerical information and are more likely to give incorrect answers when disturbed by irrelevant numerical information. The higher the perturbation intensity, the more obvious these defects are. At the same time, in the absence of core questioning instruction, models can still maintain an accuracy of 20%-40%, indicating that LLMs may rely on memory templates or pattern matching to complete the task, rather than logical reasoning. In general, our work reveals the shortcomings and limitations of current LLMs in their reasoning capabilities, which is of great significance for the further development of LLMs.

MSCR: Exploring the Vulnerability of LLMs' Mathematical Reasoning Abilities Using Multi-Source Candidate Replacement

LLMs demonstrate performance comparable to human abilities in complex tasks such as mathematical reasoning, but their robustness in mathematical reasoning under minor input perturbations still lacks systematic investigation. Existing methods generally suffer from limited scalability, weak semantic preservation, and high costs. Therefore, we propose MSCR, an automated adversarial attack method based on multi-source candidate replacement. By combining three information sources including cosine similarity in the embedding space of LLMs, the WordNet dictionary, and contextual predictions from a masked language model, we generate for each word in the input question a set of semantically similar candidates, which are then filtered and substituted one by one to carry out the attack. We conduct large-scale experiments on LLMs using the GSM8K and MATH500 benchmarks. The results show that even a slight perturbation involving only a single word can significantly reduce the accuracy of all models, with the maximum drop reaching 49.89% on GSM8K and 35.40% on MATH500, while preserving the high semantic consistency of the perturbed questions. Further analysis reveals that perturbations not only lead to incorrect outputs but also substantially increase the average response length, which results in more redundant reasoning paths and higher computational resource consumption. These findings highlight the robustness deficiencies and efficiency bottlenecks of current LLMs in mathematical reasoning tasks.

Frustratingly Easy Task-aware Pruning for Large Language Models

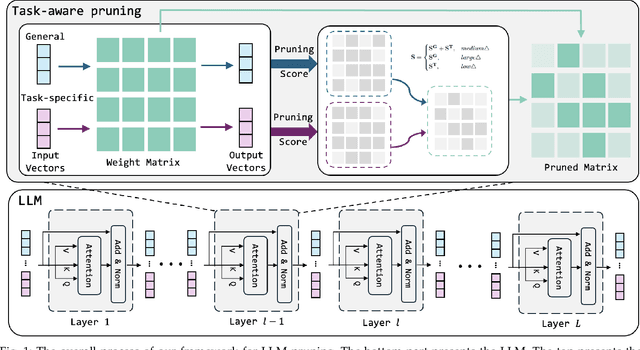
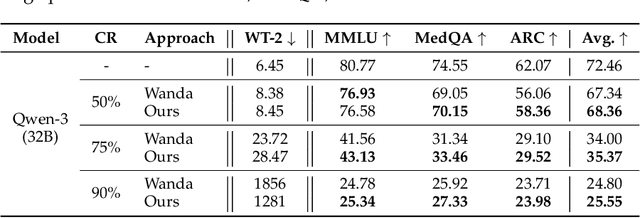
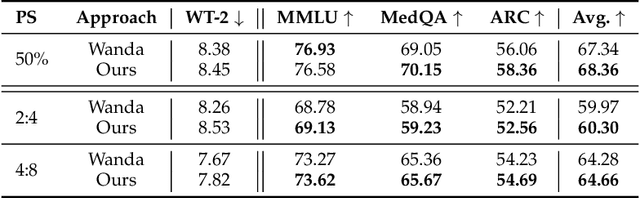
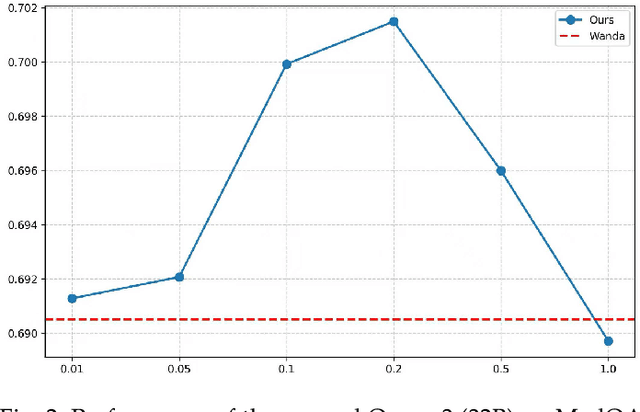
Pruning provides a practical solution to reduce the resources required to run large language models (LLMs) to benefit from their effective capabilities as well as control their cost for training and inference. Research on LLM pruning often ranks the importance of LLM parameters using their magnitudes and calibration-data activations and removes (or masks) the less important ones, accordingly reducing LLMs' size. However, these approaches primarily focus on preserving the LLM's ability to generate fluent sentences, while neglecting performance on specific domains and tasks. In this paper, we propose a simple yet effective pruning approach for LLMs that preserves task-specific capabilities while shrinking their parameter space. We first analyze how conventional pruning minimizes loss perturbation under general-domain calibration and extend this formulation by incorporating task-specific feature distributions into the importance computation of existing pruning algorithms. Thus, our framework computes separate importance scores using both general and task-specific calibration data, partitions parameters into shared and exclusive groups based on activation-norm differences, and then fuses their scores to guide the pruning process. This design enables our method to integrate seamlessly with various foundation pruning techniques and preserve the LLM's specialized abilities under compression. Experiments on widely used benchmarks demonstrate that our approach is effective and consistently outperforms the baselines with identical pruning ratios and different settings.

FZOO: Fast Zeroth-Order Optimizer for Fine-Tuning Large Language Models towards Adam-Scale Speed

Fine-tuning large language models (LLMs) often faces GPU memory bottlenecks: the backward pass of first-order optimizers like Adam increases memory usage to more than 10 times the inference level (e.g., 633 GB for OPT-30B). Zeroth-order (ZO) optimizers avoid this cost by estimating gradients only from forward passes, yet existing methods like MeZO usually require many more steps to converge. Can this trade-off between speed and memory in ZO be fundamentally improved? Normalized-SGD demonstrates strong empirical performance with greater memory efficiency than Adam. In light of this, we introduce FZOO, a Fast Zeroth-Order Optimizer toward Adam-Scale Speed. FZOO reduces the total forward passes needed for convergence by employing batched one-sided estimates that adapt step sizes based on the standard deviation of batch losses. It also accelerates per-batch computation through the use of Rademacher random vector perturbations coupled with CUDA's parallel processing. Extensive experiments on diverse models, including RoBERTa-large, OPT (350M-66B), Phi-2, and Llama3, across 11 tasks validate FZOO's effectiveness. On average, FZOO outperforms MeZO by 3 percent in accuracy while requiring 3 times fewer forward passes. For RoBERTa-large, FZOO achieves average improvements of 5.6 percent in accuracy and an 18 times reduction in forward passes compared to MeZO, achieving convergence speeds comparable to Adam. We also provide theoretical analysis proving FZOO's formal equivalence to a normalized-SGD update rule and its convergence guarantees. FZOO integrates smoothly into PEFT techniques, enabling even larger memory savings. Overall, our results make single-GPU, high-speed, full-parameter fine-tuning practical and point toward future work on memory-efficient pre-training.

Towards Understanding The Calibration Benefits of Sharpness-Aware Minimization

Deep neural networks have been increasingly used in safety-critical applications such as medical diagnosis and autonomous driving. However, many studies suggest that they are prone to being poorly calibrated and have a propensity for overconfidence, which may have disastrous consequences. In this paper, unlike standard training such as stochastic gradient descent, we show that the recently proposed sharpness-aware minimization (SAM) counteracts this tendency towards overconfidence. The theoretical analysis suggests that SAM allows us to learn models that are already well-calibrated by implicitly maximizing the entropy of the predictive distribution. Inspired by this finding, we further propose a variant of SAM, coined as CSAM, to ameliorate model calibration. Extensive experiments on various datasets, including ImageNet-1K, demonstrate the benefits of SAM in reducing calibration error. Meanwhile, CSAM performs even better than SAM and consistently achieves lower calibration error than other approaches

An Enhanced Zeroth-Order Stochastic Frank-Wolfe Framework for Constrained Finite-Sum Optimization

We propose an enhanced zeroth-order stochastic Frank-Wolfe framework to address constrained finite-sum optimization problems, a structure prevalent in large-scale machine-learning applications. Our method introduces a novel double variance reduction framework that effectively reduces the gradient approximation variance induced by zeroth-order oracles and the stochastic sampling variance from finite-sum objectives. By leveraging this framework, our algorithm achieves significant improvements in query efficiency, making it particularly well-suited for high-dimensional optimization tasks. Specifically, for convex objectives, the algorithm achieves a query complexity of O(d \sqrt{n}/\epsilon ) to find an epsilon-suboptimal solution, where d is the dimensionality and n is the number of functions in the finite-sum objective. For non-convex objectives, it achieves a query complexity of O(d^{3/2}\sqrt{n}/\epsilon^2 ) without requiring the computation ofd partial derivatives at each iteration. These complexities are the best known among zeroth-order stochastic Frank-Wolfe algorithms that avoid explicit gradient calculations. Empirical experiments on convex and non-convex machine learning tasks, including sparse logistic regression, robust classification, and adversarial attacks on deep networks, validate the computational efficiency and scalability of our approach. Our algorithm demonstrates superior performance in both convergence rate and query complexity compared to existing methods.

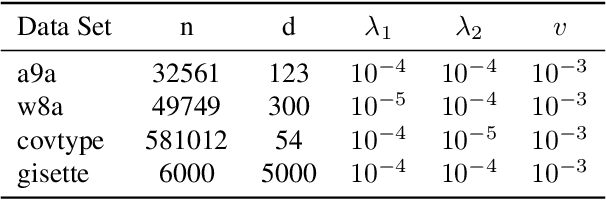
Double Variance Reduction: A Smoothing Trick for Composite Optimization Problems without First-Order Gradient

Variance reduction techniques are designed to decrease the sampling variance, thereby accelerating convergence rates of first-order (FO) and zeroth-order (ZO) optimization methods. However, in composite optimization problems, ZO methods encounter an additional variance called the coordinate-wise variance, which stems from the random gradient estimation. To reduce this variance, prior works require estimating all partial derivatives, essentially approximating FO information. This approach demands O(d) function evaluations (d is the dimension size), which incurs substantial computational costs and is prohibitive in high-dimensional scenarios. This paper proposes the Zeroth-order Proximal Double Variance Reduction (ZPDVR) method, which utilizes the averaging trick to reduce both sampling and coordinate-wise variances. Compared to prior methods, ZPDVR relies solely on random gradient estimates, calls the stochastic zeroth-order oracle (SZO) in expectation $\mathcal{O}(1)$ times per iteration, and achieves the optimal $\mathcal{O}(d(n + \kappa)\log (\frac{1}{\epsilon}))$ SZO query complexity in the strongly convex and smooth setting, where $\kappa$ represents the condition number and $\epsilon$ is the desired accuracy. Empirical results validate ZPDVR's linear convergence and demonstrate its superior performance over other related methods.

Near-Optimal Distributed Minimax Optimization under the Second-Order Similarity

This paper considers the distributed convex-concave minimax optimization under the second-order similarity. We propose stochastic variance-reduced optimistic gradient sliding (SVOGS) method, which takes the advantage of the finite-sum structure in the objective by involving the mini-batch client sampling and variance reduction. We prove SVOGS can achieve the $\varepsilon$-duality gap within communication rounds of ${\mathcal O}(\delta D^2/\varepsilon)$, communication complexity of ${\mathcal O}(n+\sqrt{n}\delta D^2/\varepsilon)$, and local gradient calls of $\tilde{\mathcal O}(n+(\sqrt{n}\delta+L)D^2/\varepsilon\log(1/\varepsilon))$, where $n$ is the number of nodes, $\delta$ is the degree of the second-order similarity, $L$ is the smoothness parameter and $D$ is the diameter of the constraint set. We can verify that all of above complexity (nearly) matches the corresponding lower bounds. For the specific $\mu$-strongly-convex-$\mu$-strongly-convex case, our algorithm has the upper bounds on communication rounds, communication complexity, and local gradient calls of $\mathcal O(\delta/\mu\log(1/\varepsilon))$, ${\mathcal O}((n+\sqrt{n}\delta/\mu)\log(1/\varepsilon))$, and $\tilde{\mathcal O}(n+(\sqrt{n}\delta+L)/\mu)\log(1/\varepsilon))$ respectively, which are also nearly tight. Furthermore, we conduct the numerical experiments to show the empirical advantages of proposed method.