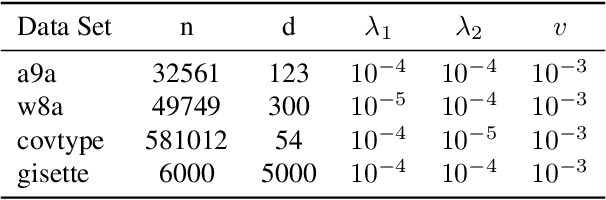
Double Variance Reduction: A Smoothing Trick for Composite Optimization Problems without First-Order Gradient

Variance reduction techniques are designed to decrease the sampling variance, thereby accelerating convergence rates of first-order (FO) and zeroth-order (ZO) optimization methods. However, in composite optimization problems, ZO methods encounter an additional variance called the coordinate-wise variance, which stems from the random gradient estimation. To reduce this variance, prior works require estimating all partial derivatives, essentially approximating FO information. This approach demands O(d) function evaluations (d is the dimension size), which incurs substantial computational costs and is prohibitive in high-dimensional scenarios. This paper proposes the Zeroth-order Proximal Double Variance Reduction (ZPDVR) method, which utilizes the averaging trick to reduce both sampling and coordinate-wise variances. Compared to prior methods, ZPDVR relies solely on random gradient estimates, calls the stochastic zeroth-order oracle (SZO) in expectation $\mathcal{O}(1)$ times per iteration, and achieves the optimal $\mathcal{O}(d(n + \kappa)\log (\frac{1}{\epsilon}))$ SZO query complexity in the strongly convex and smooth setting, where $\kappa$ represents the condition number and $\epsilon$ is the desired accuracy. Empirical results validate ZPDVR's linear convergence and demonstrate its superior performance over other related methods.

PPFL: A Personalized Federated Learning Framework for Heterogeneous Population

Personalization aims to characterize individual preferences and is widely applied across many fields. However, conventional personalized methods operate in a centralized manner and potentially expose the raw data when pooling individual information. In this paper, with privacy considerations, we develop a flexible and interpretable personalized framework within the paradigm of Federated Learning, called PPFL (Population Personalized Federated Learning). By leveraging canonical models to capture fundamental characteristics among the heterogeneous population and employing membership vectors to reveal clients' preferences, it models the heterogeneity as clients' varying preferences for these characteristics and provides substantial insights into client characteristics, which is lacking in existing Personalized Federated Learning (PFL) methods. Furthermore, we explore the relationship between our method and three main branches of PFL methods: multi-task PFL, clustered FL, and decoupling PFL, and demonstrate the advantages of PPFL. To solve PPFL (a non-convex constrained optimization problem), we propose a novel random block coordinate descent algorithm and present the convergence property. We conduct experiments on both pathological and practical datasets, and the results validate the effectiveness of PPFL.

Displacement field calculation of large-scale structures using computer vision with physical constraints

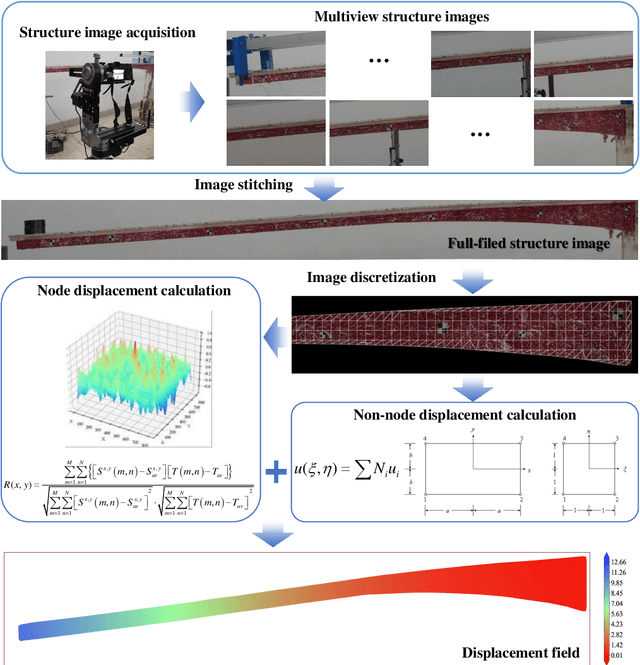
Because of the advantages of easy deployment, low cost and non-contact, computer vision-based structural displacement acquisition technique has received wide attention and research in recent years. However, the displacement field acquisition of large-scale structures is a challenging topic due to the contradiction of camera field of view and resolution. This paper presents a large-scale structural displacement field calculation framework with integrated computer vision and physical constraints using only one camera. Firstly, the full-field image of the large-scale structure is obtained by processing the multi-view image using image stitching technique; secondly, the full-field image is meshed and the node displacements are calculated using an improved template matching method; and finally, the non-node displacements are described using shape functions considering physical constraints. The developed framework was validated using a scaled bridge model and evaluated by the proposed evaluation index for displacement field calculation accuracy. This paper can provide an effective way to obtain displacement fields of large-scale structures efficiently and cost-effectively.