Near-Optimal Distributed Minimax Optimization under the Second-Order Similarity

This paper considers the distributed convex-concave minimax optimization under the second-order similarity. We propose stochastic variance-reduced optimistic gradient sliding (SVOGS) method, which takes the advantage of the finite-sum structure in the objective by involving the mini-batch client sampling and variance reduction. We prove SVOGS can achieve the $\varepsilon$-duality gap within communication rounds of ${\mathcal O}(\delta D^2/\varepsilon)$, communication complexity of ${\mathcal O}(n+\sqrt{n}\delta D^2/\varepsilon)$, and local gradient calls of $\tilde{\mathcal O}(n+(\sqrt{n}\delta+L)D^2/\varepsilon\log(1/\varepsilon))$, where $n$ is the number of nodes, $\delta$ is the degree of the second-order similarity, $L$ is the smoothness parameter and $D$ is the diameter of the constraint set. We can verify that all of above complexity (nearly) matches the corresponding lower bounds. For the specific $\mu$-strongly-convex-$\mu$-strongly-convex case, our algorithm has the upper bounds on communication rounds, communication complexity, and local gradient calls of $\mathcal O(\delta/\mu\log(1/\varepsilon))$, ${\mathcal O}((n+\sqrt{n}\delta/\mu)\log(1/\varepsilon))$, and $\tilde{\mathcal O}(n+(\sqrt{n}\delta+L)/\mu)\log(1/\varepsilon))$ respectively, which are also nearly tight. Furthermore, we conduct the numerical experiments to show the empirical advantages of proposed method.

Federated Reinforcement Learning: Techniques, Applications, and Open Challenges

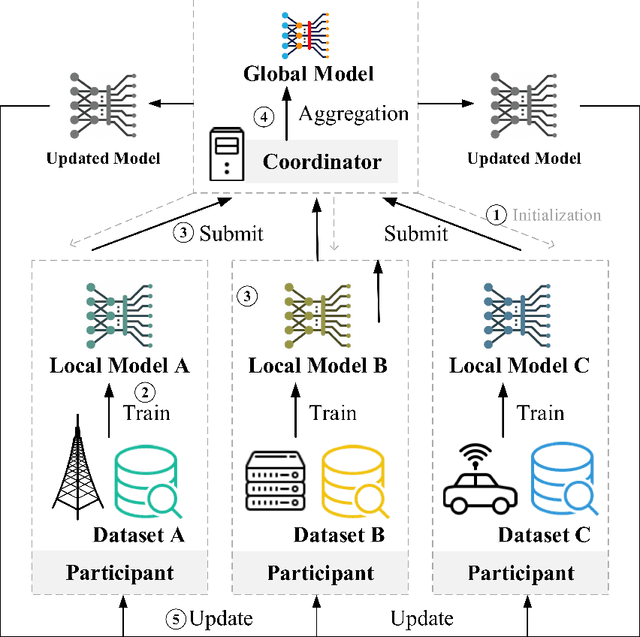
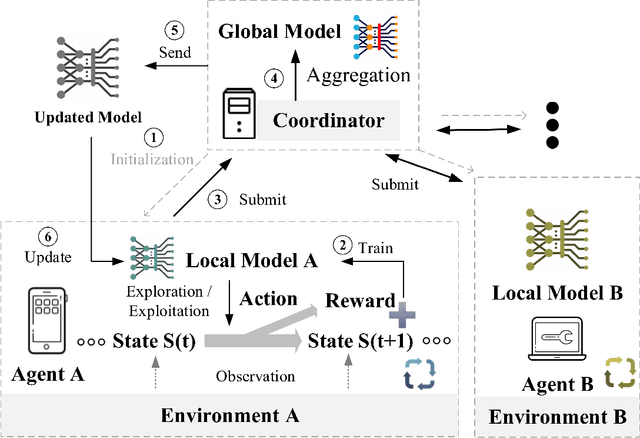
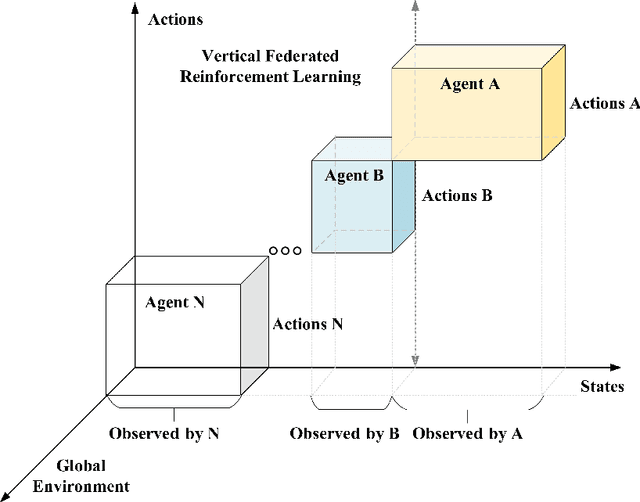
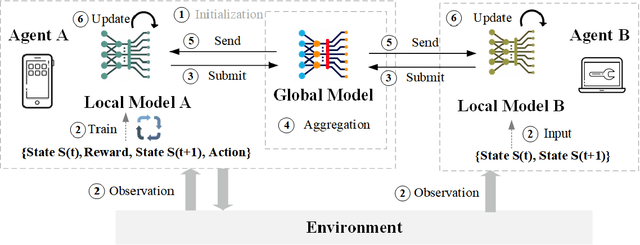
This paper presents a comprehensive survey of Federated Reinforcement Learning (FRL), an emerging and promising field in Reinforcement Learning (RL). Starting with a tutorial of Federated Learning (FL) and RL, we then focus on the introduction of FRL as a new method with great potential by leveraging the basic idea of FL to improve the performance of RL while preserving data-privacy. According to the distribution characteristics of the agents in the framework, FRL algorithms can be divided into two categories, i.e. Horizontal Federated Reinforcement Learning (HFRL) and Vertical Federated Reinforcement Learning (VFRL). We provide the detailed definitions of each category by formulas, investigate the evolution of FRL from a technical perspective, and highlight its advantages over previous RL algorithms. In addition, the existing works on FRL are summarized by application fields, including edge computing, communication, control optimization, and attack detection. Finally, we describe and discuss several key research directions that are crucial to solving the open problems within FRL.