Stabilizing Sharpness-aware Minimization Through A Simple Renormalization Strategy

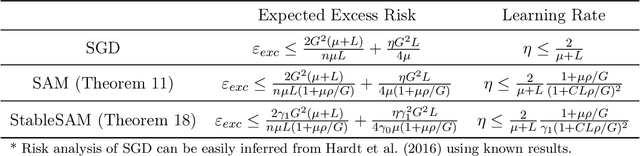
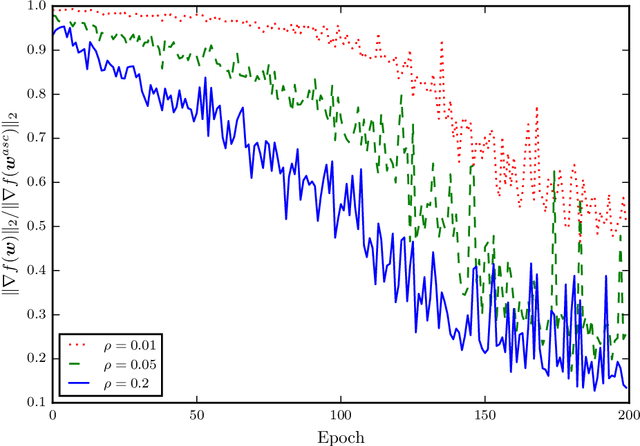
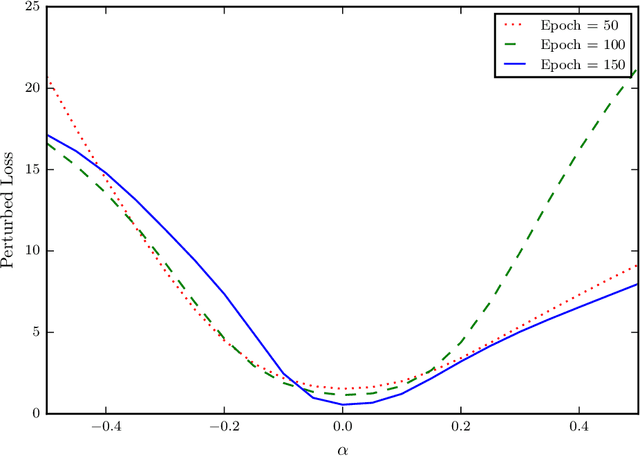
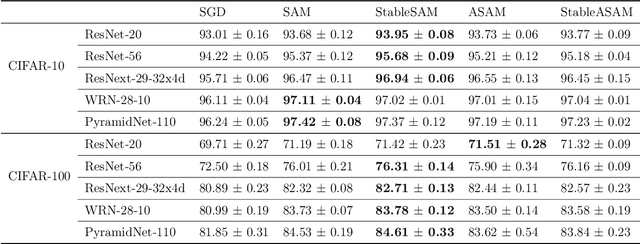
Recently, sharpness-aware minimization (SAM) has attracted a lot of attention because of its surprising effectiveness in improving generalization performance.However, training neural networks with SAM can be highly unstable since the loss does not decrease along the direction of the exact gradient at the current point, but instead follows the direction of a surrogate gradient evaluated at another point nearby. To address this issue, we propose a simple renormalization strategy, dubbed StableSAM, so that the norm of the surrogate gradient maintains the same as that of the exact gradient. Our strategy is easy to implement and flexible enough to integrate with SAM and its variants, almost at no computational cost. With elementary tools from convex optimization and learning theory, we also conduct a theoretical analysis of sharpness-aware training, revealing that compared to stochastic gradient descent (SGD), the effectiveness of SAM is only assured in a limited regime of learning rate. In contrast, we show how StableSAM extends this regime of learning rate and when it can consistently perform better than SAM with minor modification. Finally, we demonstrate the improved performance of StableSAM on several representative data sets and tasks.

Seismic Data Interpolation based on Denoising Diffusion Implicit Models with Resampling

The incompleteness of the seismic data caused by missing traces along the spatial extension is a common issue in seismic acquisition due to the existence of obstacles and economic constraints, which severely impairs the imaging quality of subsurface geological structures. Recently, deep learningbased seismic interpolation methods have attained promising progress, while achieving stable training of generative adversarial networks is not easy, and performance degradation is usually notable if the missing patterns in the testing and training do not match. In this paper, we propose a novel seismic denoising diffusion implicit model with resampling. The model training is established on the denoising diffusion probabilistic model, where U-Net is equipped with the multi-head self-attention to match the noise in each step. The cosine noise schedule, serving as the global noise configuration, promotes the high utilization of known trace information by accelerating the passage of the excessive noise stages. The model inference utilizes the denoising diffusion implicit model, conditioning on the known traces, to enable high-quality interpolation with fewer diffusion steps. To enhance the coherency between the known traces and the missing traces within each reverse step, the inference process integrates a resampling strategy to achieve an information recap on the former interpolated traces. Extensive experiments conducted on synthetic and field seismic data validate the superiority of our model and its robustness to various missing patterns. In addition, uncertainty quantification and ablation studies are also investigated.

Spherical Space Feature Decomposition for Guided Depth Map Super-Resolution

Guided depth map super-resolution (GDSR), as a hot topic in multi-modal image processing, aims to upsample low-resolution (LR) depth maps with additional information involved in high-resolution (HR) RGB images from the same scene. The critical step of this task is to effectively extract domain-shared and domain-private RGB/depth features. In addition, three detailed issues, namely blurry edges, noisy surfaces, and over-transferred RGB texture, need to be addressed. In this paper, we propose the Spherical Space feature Decomposition Network (SSDNet) to solve the above issues. To better model cross-modality features, Restormer block-based RGB/depth encoders are employed for extracting local-global features. Then, the extracted features are mapped to the spherical space to complete the separation of private features and the alignment of shared features. Shared features of RGB are fused with the depth features to complete the GDSR task. Subsequently, a spherical contrast refinement (SCR) module is proposed to further address the detail issues. Patches that are classified according to imperfect categories are input to the SCR module, where the patch features are pulled closer to the ground truth and pushed away from the corresponding imperfect samples in the spherical feature space via contrastive learning. Extensive experiments demonstrate that our method can achieve state-of-the-art results on four test datasets and can successfully generalize to real-world scenes. Code will be released.

Trajectory-dependent Generalization Bounds for Deep Neural Networks via Fractional Brownian Motion

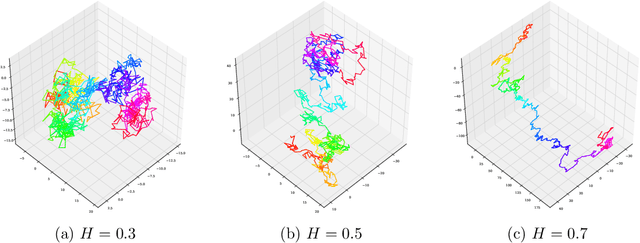
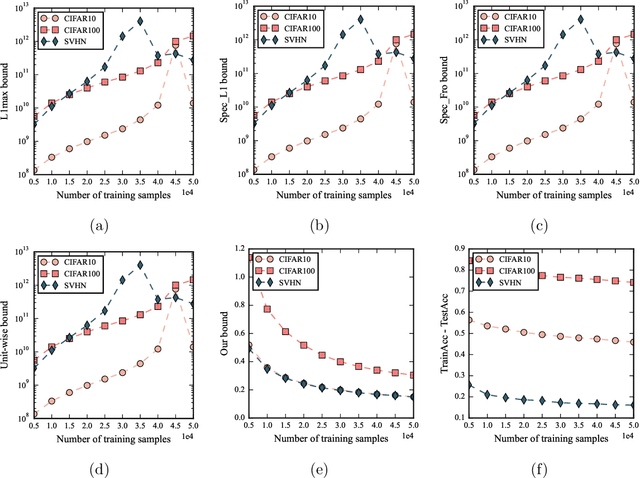
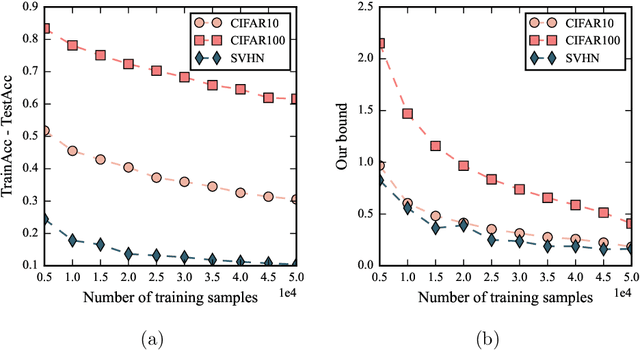
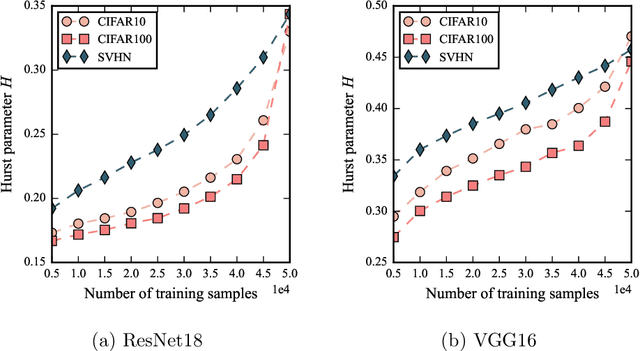
Despite being tremendously overparameterized, it is appreciated that deep neural networks trained by stochastic gradient descent (SGD) generalize surprisingly well. Based on the Rademacher complexity of a pre-specified hypothesis set, different norm-based generalization bounds have been developed to explain this phenomenon. However, recent studies suggest these bounds might be problematic as they increase with the training set size, which is contrary to empirical evidence. In this study, we argue that the hypothesis set SGD explores is trajectory-dependent and thus may provide a tighter bound over its Rademacher complexity. To this end, we characterize the SGD recursion via a stochastic differential equation by assuming the incurred stochastic gradient noise follows the fractional Brownian motion. We then identify the Rademacher complexity in terms of the covering numbers and relate it to the Hausdorff dimension of the optimization trajectory. By invoking the hypothesis set stability, we derive a novel generalization bound for deep neural networks. Extensive experiments demonstrate that it predicts well the generalization gap over several common experimental interventions. We further show that the Hurst parameter of the fractional Brownian motion is more informative than existing generalization indicators such as the power-law index and the upper Blumenthal-Getoor index.

Understanding Long Range Memory Effects in Deep Neural Networks

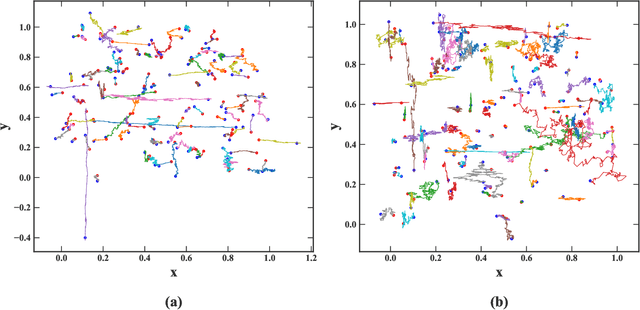
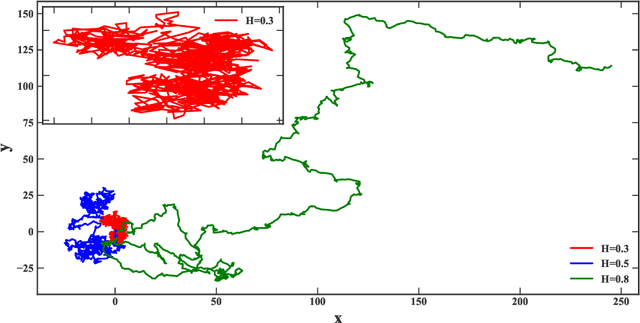
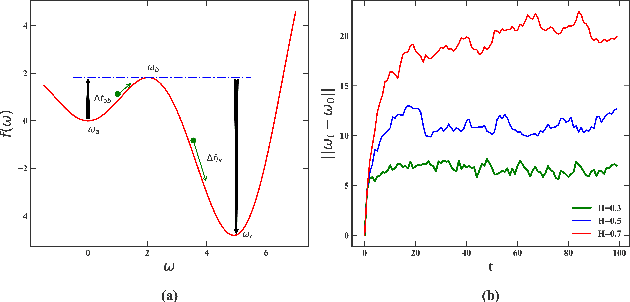
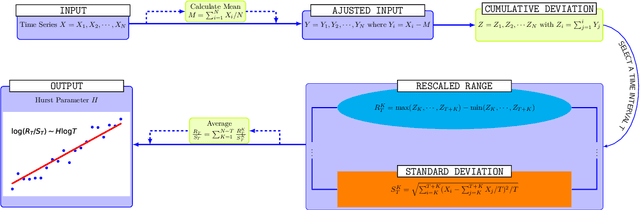
\textit{Stochastic gradient descent} (SGD) is of fundamental importance in deep learning. Despite its simplicity, elucidating its efficacy remains challenging. Conventionally, the success of SGD is attributed to the \textit{stochastic gradient noise} (SGN) incurred in the training process. Based on this general consensus, SGD is frequently treated and analyzed as the Euler-Maruyama discretization of a \textit{stochastic differential equation} (SDE) driven by either Brownian or L\'evy stable motion. In this study, we argue that SGN is neither Gaussian nor stable. Instead, inspired by the long-time correlation emerging in SGN series, we propose that SGD can be viewed as a discretization of an SDE driven by \textit{fractional Brownian motion} (FBM). Accordingly, the different convergence behavior of SGD dynamics is well grounded. Moreover, the first passage time of an SDE driven by FBM is approximately derived. This indicates a lower escaping rate for a larger Hurst parameter, and thus SGD stays longer in flat minima. This happens to coincide with the well-known phenomenon that SGD favors flat minima that generalize well. Four groups of experiments are conducted to validate our conjecture, and it is demonstrated that long-range memory effects persist across various model architectures, datasets, and training strategies. Our study opens up a new perspective and may contribute to a better understanding of SGD.