Understanding Long Range Memory Effects in Deep Neural Networks

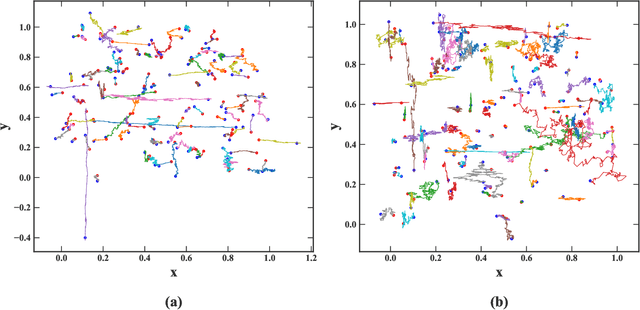
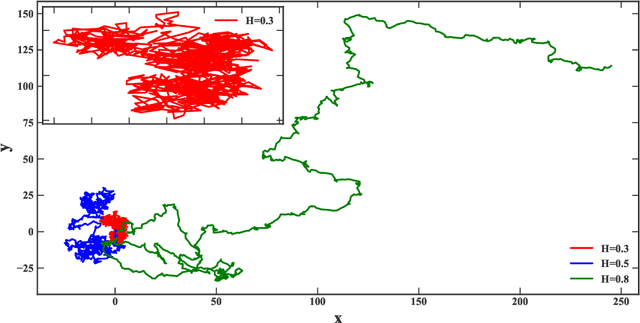
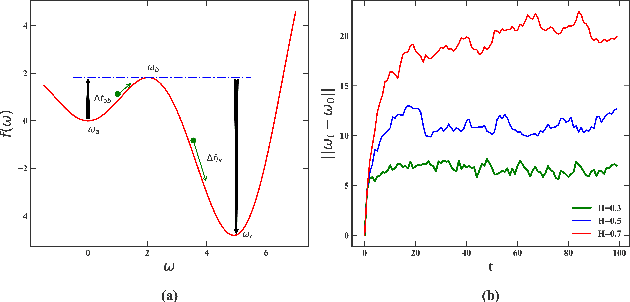
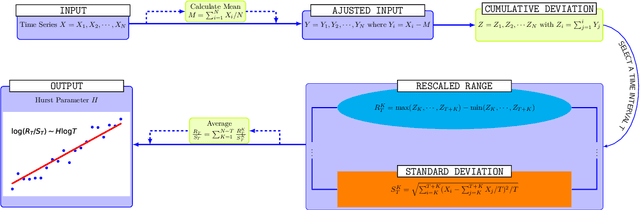
\textit{Stochastic gradient descent} (SGD) is of fundamental importance in deep learning. Despite its simplicity, elucidating its efficacy remains challenging. Conventionally, the success of SGD is attributed to the \textit{stochastic gradient noise} (SGN) incurred in the training process. Based on this general consensus, SGD is frequently treated and analyzed as the Euler-Maruyama discretization of a \textit{stochastic differential equation} (SDE) driven by either Brownian or L\'evy stable motion. In this study, we argue that SGN is neither Gaussian nor stable. Instead, inspired by the long-time correlation emerging in SGN series, we propose that SGD can be viewed as a discretization of an SDE driven by \textit{fractional Brownian motion} (FBM). Accordingly, the different convergence behavior of SGD dynamics is well grounded. Moreover, the first passage time of an SDE driven by FBM is approximately derived. This indicates a lower escaping rate for a larger Hurst parameter, and thus SGD stays longer in flat minima. This happens to coincide with the well-known phenomenon that SGD favors flat minima that generalize well. Four groups of experiments are conducted to validate our conjecture, and it is demonstrated that long-range memory effects persist across various model architectures, datasets, and training strategies. Our study opens up a new perspective and may contribute to a better understanding of SGD.