Trajectory-dependent Generalization Bounds for Deep Neural Networks via Fractional Brownian Motion
Paper and Code
Jun 09, 2022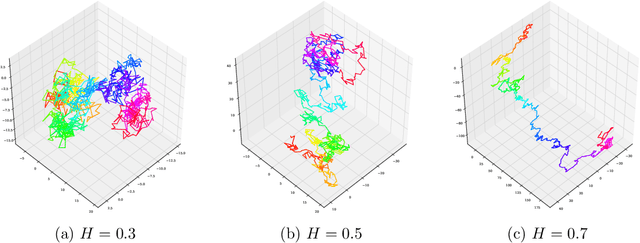
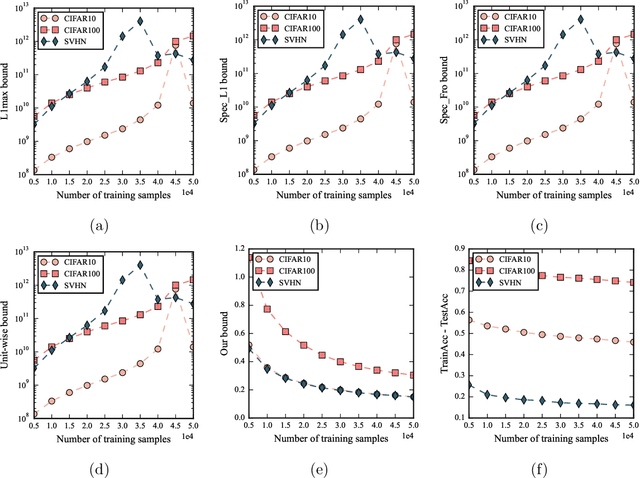
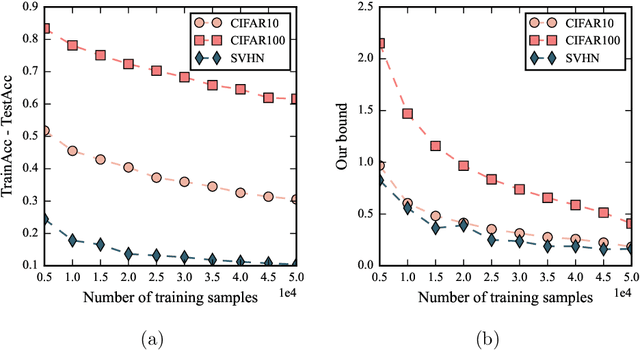
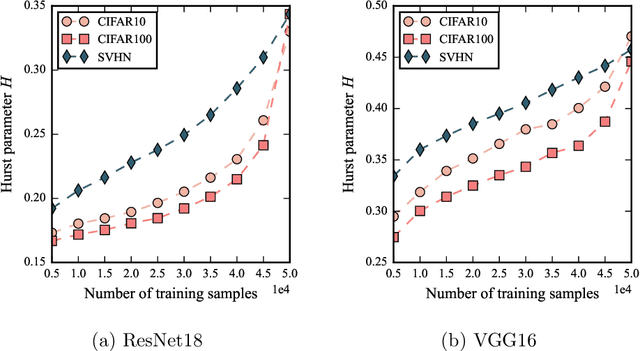
Despite being tremendously overparameterized, it is appreciated that deep neural networks trained by stochastic gradient descent (SGD) generalize surprisingly well. Based on the Rademacher complexity of a pre-specified hypothesis set, different norm-based generalization bounds have been developed to explain this phenomenon. However, recent studies suggest these bounds might be problematic as they increase with the training set size, which is contrary to empirical evidence. In this study, we argue that the hypothesis set SGD explores is trajectory-dependent and thus may provide a tighter bound over its Rademacher complexity. To this end, we characterize the SGD recursion via a stochastic differential equation by assuming the incurred stochastic gradient noise follows the fractional Brownian motion. We then identify the Rademacher complexity in terms of the covering numbers and relate it to the Hausdorff dimension of the optimization trajectory. By invoking the hypothesis set stability, we derive a novel generalization bound for deep neural networks. Extensive experiments demonstrate that it predicts well the generalization gap over several common experimental interventions. We further show that the Hurst parameter of the fractional Brownian motion is more informative than existing generalization indicators such as the power-law index and the upper Blumenthal-Getoor index.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge