Derivative-Informed Fourier Neural Operator: Universal Approximation and Applications to PDE-Constrained Optimization

We present approximation theories and efficient training methods for derivative-informed Fourier neural operators (DIFNOs) with applications to PDE-constrained optimization. A DIFNO is an FNO trained by minimizing its prediction error jointly on output and Fréchet derivative samples of a high-fidelity operator (e.g., a parametric PDE solution operator). As a result, a DIFNO can closely emulate not only the high-fidelity operator's response but also its sensitivities. To motivate the use of DIFNOs instead of conventional FNOs as surrogate models, we show that accurate surrogate-driven PDE-constrained optimization requires accurate surrogate Fréchet derivatives. Then, for continuously differentiable operators, we establish (i) simultaneous universal approximation of FNOs and their Fréchet derivatives on compact sets, and (ii) universal approximation of FNOs in weighted Sobolev spaces with input measures that have unbounded supports. Our theoretical results certify the capability of FNOs for accurate derivative-informed operator learning and accurate solution of PDE-constrained optimization. Furthermore, we develop efficient training schemes using dimension reduction and multi-resolution techniques that significantly reduce memory and computational costs for Fréchet derivative learning. Numerical examples on nonlinear diffusion--reaction, Helmholtz, and Navier--Stokes equations demonstrate that DIFNOs are superior in sample complexity for operator learning and solving infinite-dimensional PDE-constrained inverse problems, achieving high accuracy at low training sample sizes.

Faster Stochastic Algorithms for Minimax Optimization under Polyak--Łojasiewicz Conditions

This paper considers stochastic first-order algorithms for minimax optimization under Polyak--{\L}ojasiewicz (PL) conditions. We propose SPIDER-GDA for solving the finite-sum problem of the form $\min_x \max_y f(x,y)\triangleq \frac{1}{n} \sum_{i=1}^n f_i(x,y)$, where the objective function $f(x,y)$ is $\mu_x$-PL in $x$ and $\mu_y$-PL in $y$; and each $f_i(x,y)$ is $L$-smooth. We prove SPIDER-GDA could find an $\epsilon$-optimal solution within ${\mathcal O}\left((n + \sqrt{n}\,\kappa_x\kappa_y^2)\log (1/\epsilon)\right)$ stochastic first-order oracle (SFO) complexity, which is better than the state-of-the-art method whose SFO upper bound is ${\mathcal O}\big((n + n^{2/3}\kappa_x\kappa_y^2)\log (1/\epsilon)\big)$, where $\kappa_x\triangleq L/\mu_x$ and $\kappa_y\triangleq L/\mu_y$. For the ill-conditioned case, we provide an accelerated algorithm to reduce the computational cost further. It achieves $\tilde{{\mathcal O}}\big((n+\sqrt{n}\,\kappa_x\kappa_y)\log^2 (1/\epsilon)\big)$ SFO upper bound when $\kappa_y \gtrsim \sqrt{n}$. Our ideas also can be applied to the more general setting that the objective function only satisfies PL condition for one variable. Numerical experiments validate the superiority of proposed methods.

Colossal-Auto: Unified Automation of Parallelization and Activation Checkpoint for Large-scale Models

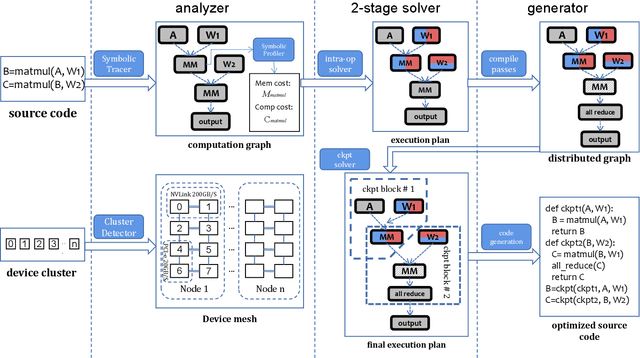
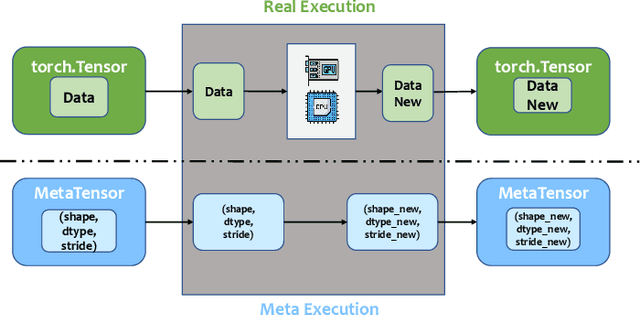
In recent years, large-scale models have demonstrated state-of-the-art performance across various domains. However, training such models requires various techniques to address the problem of limited computing power and memory on devices such as GPUs. Some commonly used techniques include pipeline parallelism, tensor parallelism, and activation checkpointing. While existing works have focused on finding efficient distributed execution plans (Zheng et al. 2022) and activation checkpoint scheduling (Herrmann et al. 2019, Beaumont et al. 2021}, there has been no method proposed to optimize these two plans jointly. Moreover, ahead-of-time compilation relies heavily on accurate memory and computing overhead estimation, which is often time-consuming and misleading. Existing training systems and machine learning pipelines either physically execute each operand or estimate memory usage with a scaled input tensor. To address these challenges, we introduce a system that can jointly optimize distributed execution and gradient checkpointing plans. Additionally, we provide an easy-to-use symbolic profiler that generates memory and computing statistics for any PyTorch model with a minimal time cost. Our approach allows users to parallelize their model training on the given hardware with minimum code change based. The source code is publicly available at Colossal-AI GitHub or https://github.com/hpcaitech/ColossalAI