Incremental Gauss--Newton Methods with Superlinear Convergence Rates

This paper addresses the challenge of solving large-scale nonlinear equations with H\"older continuous Jacobians. We introduce a novel Incremental Gauss--Newton (IGN) method within explicit superlinear convergence rate, which outperforms existing methods that only achieve linear convergence rate. In particular, we formulate our problem by the nonlinear least squares with finite-sum structure, and our method incrementally iterates with the information of one component in each round. We also provide a mini-batch extension to our IGN method that obtains an even faster superlinear convergence rate. Furthermore, we conduct numerical experiments to show the advantages of the proposed methods.

Differentiable Cluster Graph Neural Network

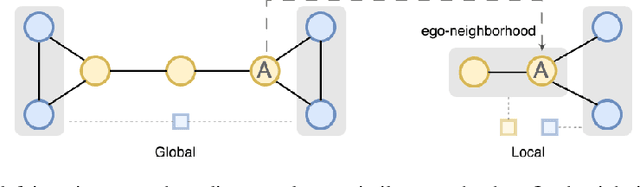
Graph Neural Networks often struggle with long-range information propagation and in the presence of heterophilous neighborhoods. We address both challenges with a unified framework that incorporates a clustering inductive bias into the message passing mechanism, using additional cluster-nodes. Central to our approach is the formulation of an optimal transport based implicit clustering objective function. However, the algorithm for solving the implicit objective function needs to be differentiable to enable end-to-end learning of the GNN. To facilitate this, we adopt an entropy regularized objective function and propose an iterative optimization process, alternating between solving for the cluster assignments and updating the node/cluster-node embeddings. Notably, our derived closed-form optimization steps are themselves simple yet elegant message passing steps operating seamlessly on a bipartite graph of nodes and cluster-nodes. Our clustering-based approach can effectively capture both local and global information, demonstrated by extensive experiments on both heterophilous and homophilous datasets.

Incremental Quasi-Newton Methods with Faster Superlinear Convergence Rates

We consider the finite-sum optimization problem, where each component function is strongly convex and has Lipschitz continuous gradient and Hessian. The recently proposed incremental quasi-Newton method is based on BFGS update and achieves a local superlinear convergence rate that is dependent on the condition number of the problem. This paper proposes a more efficient quasi-Newton method by incorporating the symmetric rank-1 update into the incremental framework, which results in the condition-number-free local superlinear convergence rate. Furthermore, we can boost our method by applying the block update on the Hessian approximation, which leads to an even faster local convergence rate. The numerical experiments show the proposed methods significantly outperform the baseline methods.

Decentralized Sum-of-Nonconvex Optimization

We consider the optimization problem of minimizing the sum-of-nonconvex function, i.e., a convex function that is the average of nonconvex components. The existing stochastic algorithms for such a problem only focus on a single machine and the centralized scenario. In this paper, we study the sum-of-nonconvex optimization in the decentralized setting. We present a new theoretical analysis of the PMGT-SVRG algorithm for this problem and prove the linear convergence of their approach. However, the convergence rate of the PMGT-SVRG algorithm has a linear dependency on the condition number, which is undesirable for the ill-conditioned problem. To remedy this issue, we propose an accelerated stochastic decentralized first-order algorithm by incorporating the techniques of acceleration, gradient tracking, and multi-consensus mixing into the SVRG algorithm. The convergence rate of the proposed method has a square-root dependency on the condition number. The numerical experiments validate the theoretical guarantee of our proposed algorithms on both synthetic and real-world datasets.

Towards Sharper First-Order Adversary with Quantized Gradients

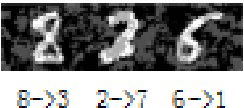
Despite the huge success of Deep Neural Networks (DNNs) in a wide spectrum of machine learning and data mining tasks, recent research shows that this powerful tool is susceptible to maliciously crafted adversarial examples. Up until now, adversarial training has been the most successful defense against adversarial attacks. To increase adversarial robustness, a DNN can be trained with a combination of benign and adversarial examples generated by first-order methods. However, in state-of-the-art first-order attacks, adversarial examples with sign gradients retain the sign information of each gradient component but discard the relative magnitude between components. In this work, we replace sign gradients with quantized gradients. Gradient quantization not only preserves the sign information, but also keeps the relative magnitude between components. Experiments show white-box first-order attacks with quantized gradients outperform their variants with sign gradients on multiple datasets. Notably, our BLOB\_QG attack achieves an accuracy of $88.32\%$ on the secret MNIST model from the MNIST Challenge and it outperforms all other methods on the leaderboard of white-box attacks.