Hierarchical Neural Constructive Solver for Real-world TSP Scenarios

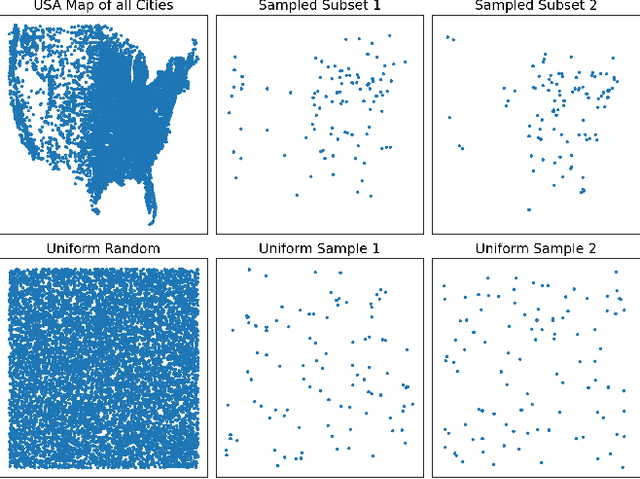
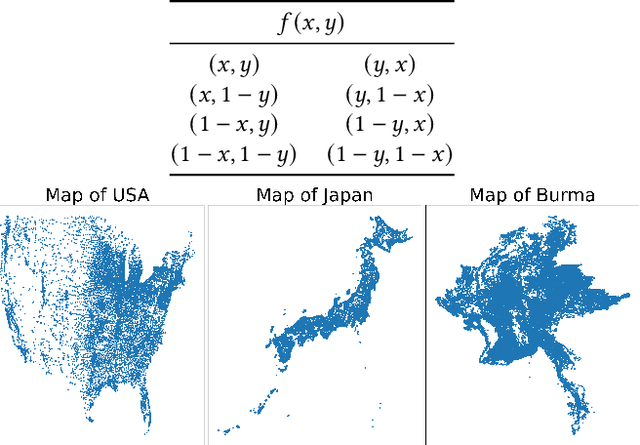
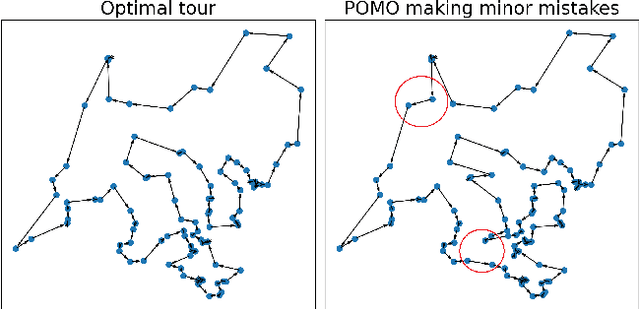
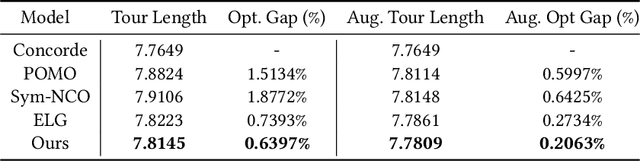
Existing neural constructive solvers for routing problems have predominantly employed transformer architectures, conceptualizing the route construction as a set-to-sequence learning task. However, their efficacy has primarily been demonstrated on entirely random problem instances that inadequately capture real-world scenarios. In this paper, we introduce realistic Traveling Salesman Problem (TSP) scenarios relevant to industrial settings and derive the following insights: (1) The optimal next node (or city) to visit often lies within proximity to the current node, suggesting the potential benefits of biasing choices based on current locations. (2) Effectively solving the TSP requires robust tracking of unvisited nodes and warrants succinct grouping strategies. Building upon these insights, we propose integrating a learnable choice layer inspired by Hypernetworks to prioritize choices based on the current location, and a learnable approximate clustering algorithm inspired by the Expectation-Maximization algorithm to facilitate grouping the unvisited cities. Together, these two contributions form a hierarchical approach towards solving the realistic TSP by considering both immediate local neighbourhoods and learning an intermediate set of node representations. Our hierarchical approach yields superior performance compared to both classical and recent transformer models, showcasing the efficacy of the key designs.

Differentiable Cluster Graph Neural Network

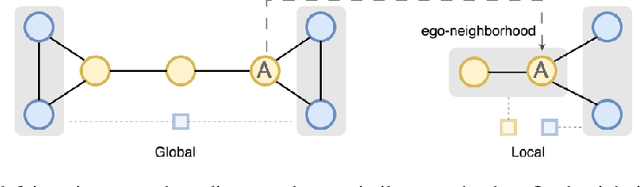
Graph Neural Networks often struggle with long-range information propagation and in the presence of heterophilous neighborhoods. We address both challenges with a unified framework that incorporates a clustering inductive bias into the message passing mechanism, using additional cluster-nodes. Central to our approach is the formulation of an optimal transport based implicit clustering objective function. However, the algorithm for solving the implicit objective function needs to be differentiable to enable end-to-end learning of the GNN. To facilitate this, we adopt an entropy regularized objective function and propose an iterative optimization process, alternating between solving for the cluster assignments and updating the node/cluster-node embeddings. Notably, our derived closed-form optimization steps are themselves simple yet elegant message passing steps operating seamlessly on a bipartite graph of nodes and cluster-nodes. Our clustering-based approach can effectively capture both local and global information, demonstrated by extensive experiments on both heterophilous and homophilous datasets.

Constrained Layout Generation with Factor Graphs

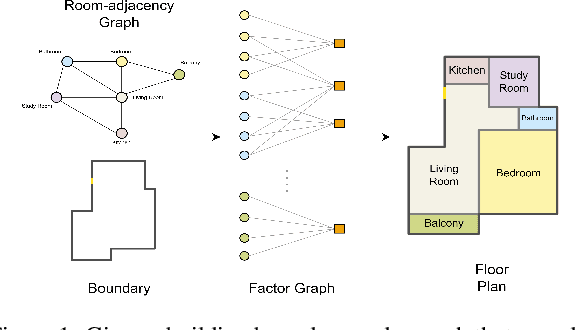
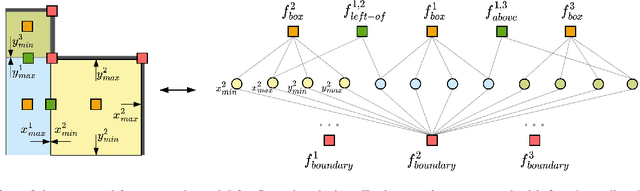
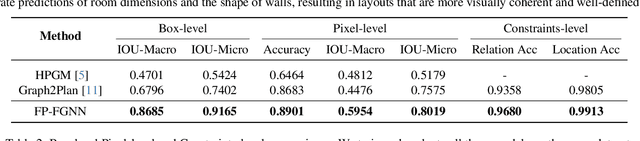
This paper addresses the challenge of object-centric layout generation under spatial constraints, seen in multiple domains including floorplan design process. The design process typically involves specifying a set of spatial constraints that include object attributes like size and inter-object relations such as relative positioning. Existing works, which typically represent objects as single nodes, lack the granularity to accurately model complex interactions between objects. For instance, often only certain parts of an object, like a room's right wall, interact with adjacent objects. To address this gap, we introduce a factor graph based approach with four latent variable nodes for each room, and a factor node for each constraint. The factor nodes represent dependencies among the variables to which they are connected, effectively capturing constraints that are potentially of a higher order. We then develop message-passing on the bipartite graph, forming a factor graph neural network that is trained to produce a floorplan that aligns with the desired requirements. Our approach is simple and generates layouts faithful to the user requirements, demonstrated by a large improvement in IOU scores over existing methods. Additionally, our approach, being inferential and accurate, is well-suited to the practical human-in-the-loop design process where specifications evolve iteratively, offering a practical and powerful tool for AI-guided design.

PF-GNN: Differentiable particle filtering based approximation of universal graph representations

Message passing Graph Neural Networks (GNNs) are known to be limited in expressive power by the 1-WL color-refinement test for graph isomorphism. Other more expressive models either are computationally expensive or need preprocessing to extract structural features from the graph. In this work, we propose to make GNNs universal by guiding the learning process with exact isomorphism solver techniques which operate on the paradigm of Individualization and Refinement (IR), a method to artificially introduce asymmetry and further refine the coloring when 1-WL stops. Isomorphism solvers generate a search tree of colorings whose leaves uniquely identify the graph. However, the tree grows exponentially large and needs hand-crafted pruning techniques which are not desirable from a learning perspective. We take a probabilistic view and approximate the search tree of colorings (i.e. embeddings) by sampling multiple paths from root to leaves of the search tree. To learn more discriminative representations, we guide the sampling process with particle filter updates, a principled approach for sequential state estimation. Our algorithm is end-to-end differentiable, can be applied with any GNN as backbone and learns richer graph representations with only linear increase in runtime. Experimental evaluation shows that our approach consistently outperforms leading GNN models on both synthetic benchmarks for isomorphism detection as well as real-world datasets.

Tell2Design: A Dataset for Language-Guided Floor Plan Generation

We consider the task of generating designs directly from natural language descriptions, and consider floor plan generation as the initial research area. Language conditional generative models have recently been very successful in generating high-quality artistic images. However, designs must satisfy different constraints that are not present in generating artistic images, particularly spatial and relational constraints. We make multiple contributions to initiate research on this task. First, we introduce a novel dataset, \textit{Tell2Design} (T2D), which contains more than $80k$ floor plan designs associated with natural language instructions. Second, we propose a Sequence-to-Sequence model that can serve as a strong baseline for future research. Third, we benchmark this task with several text-conditional image generation models. We conclude by conducting human evaluations on the generated samples and providing an analysis of human performance. We hope our contributions will propel the research on language-guided design generation forward.

Implicit Graph Neural Diffusion Based on Constrained Dirichlet Energy Minimization

Implicit graph neural networks (GNNs) have emerged as a potential approach to enable GNNs to capture long-range dependencies effectively. However, poorly designed implicit GNN layers can experience over-smoothing or may have limited adaptability to learn data geometry, potentially hindering their performance in graph learning problems. To address these issues, we introduce a geometric framework to design implicit graph diffusion layers based on a parameterized graph Laplacian operator. Our framework allows learning the geometry of vertex and edge spaces, as well as the graph gradient operator from data. We further show how implicit GNN layers can be viewed as the fixed-point solution of a Dirichlet energy minimization problem and give conditions under which it may suffer from over-smoothing. To overcome the over-smoothing problem, we design our implicit graph diffusion layer as the solution of a Dirichlet energy minimization problem with constraints on vertex features, enabling it to trade off smoothing with the preservation of node feature information. With an appropriate hyperparameter set to be larger than the largest eigenvalue of the parameterized graph Laplacian, our framework guarantees a unique equilibrium and quick convergence. Our models demonstrate better performance than leading implicit and explicit GNNs on benchmark datasets for node and graph classification tasks, with substantial accuracy improvements observed for some datasets.

Factor Graph Neural Networks

In recent years, we have witnessed a surge of Graph Neural Networks (GNNs), most of which can learn powerful representations in an end-to-end fashion with great success in many real-world applications. They have resemblance to Probabilistic Graphical Models (PGMs), but break free from some limitations of PGMs. By aiming to provide expressive methods for representation learning instead of computing marginals or most likely configurations, GNNs provide flexibility in the choice of information flowing rules while maintaining good performance. Despite their success and inspirations, they lack efficient ways to represent and learn higher-order relations among variables/nodes. More expressive higher-order GNNs which operate on k-tuples of nodes need increased computational resources in order to process higher-order tensors. We propose Factor Graph Neural Networks (FGNNs) to effectively capture higher-order relations for inference and learning. To do so, we first derive an efficient approximate Sum-Product loopy belief propagation inference algorithm for discrete higher-order PGMs. We then neuralize the novel message passing scheme into a Factor Graph Neural Network (FGNN) module by allowing richer representations of the message update rules; this facilitates both efficient inference and powerful end-to-end learning. We further show that with a suitable choice of message aggregation operators, our FGNN is also able to represent Max-Product belief propagation, providing a single family of architecture that can represent both Max and Sum-Product loopy belief propagation. Our extensive experimental evaluation on synthetic as well as real datasets demonstrates the potential of the proposed model.

Graph Representation Learning with Individualization and Refinement

Graph Neural Networks (GNNs) have emerged as prominent models for representation learning on graph structured data. GNNs follow an approach of message passing analogous to 1-dimensional Weisfeiler Lehman (1-WL) test for graph isomorphism and consequently are limited by the distinguishing power of 1-WL. More expressive higher-order GNNs which operate on k-tuples of nodes need increased computational resources in order to process higher-order tensors. Instead of the WL approach, in this work, we follow the classical approach of Individualization and Refinement (IR), a technique followed by most practical isomorphism solvers. Individualization refers to artificially distinguishing a node in the graph and refinement is the propagation of this information to other nodes through message passing. We learn to adaptively select nodes to individualize and to aggregate the resulting graphs after refinement to help handle the complexity. Our technique lets us learn richer node embeddings while keeping the computational complexity manageable. Theoretically, we show that our procedure is more expressive than the 1-WL test. Experiments show that our method outperforms prominent 1-WL GNN models as well as competitive higher-order baselines on several benchmark synthetic and real datasets. Furthermore, our method opens new doors for exploring the paradigm of learning on graph structures with individualization and refinement.

Neuralizing Efficient Higher-order Belief Propagation

Graph neural network models have been extensively used to learn node representations for graph structured data in an end-to-end setting. These models often rely on localized first order approximations of spectral graph convolutions and hence are unable to capture higher-order relational information between nodes. Probabilistic Graphical Models form another class of models that provide rich flexibility in incorporating such relational information but are limited by inefficient approximate inference algorithms at higher order. In this paper, we propose to combine these approaches to learn better node and graph representations. First, we derive an efficient approximate sum-product loopy belief propagation inference algorithm for higher-order PGMs. We then embed the message passing updates into a neural network to provide the inductive bias of the inference algorithm in end-to-end learning. This gives us a model that is flexible enough to accommodate domain knowledge while maintaining the computational advantage. We further propose methods for constructing higher-order factors that are conditioned on node and edge features and share parameters wherever necessary. Our experimental evaluation shows that our model indeed captures higher-order information, substantially outperforming state-of-the-art $k$-order graph neural networks in molecular datasets.

Visual Relationship Detection with Low Rank Non-Negative Tensor Decomposition

We address the problem of Visual Relationship Detection (VRD) which aims to describe the relationships between pairs of objects in the form of triplets of (subject, predicate, object). We observe that given a pair of bounding box proposals, objects often participate in multiple relations implying the distribution of triplets is multimodal. We leverage the strong correlations within triplets to learn the joint distribution of triplet variables conditioned on the image and the bounding box proposals, doing away with the hitherto used independent distribution of triplets. To make learning the triplet joint distribution feasible, we introduce a novel technique of learning conditional triplet distributions in the form of their normalized low rank non-negative tensor decompositions. Normalized tensor decompositions take form of mixture distributions of discrete variables and thus are able to capture multimodality. This allows us to efficiently learn higher order discrete multimodal distributions and at the same time keep the parameter size manageable. We further model the probability of selecting an object proposal pair and include a relation triplet prior in our model. We show that each part of the model improves performance and the combination outperforms state-of-the-art score on the Visual Genome (VG) and Visual Relationship Detection (VRD) datasets.