Donald Goldfarb
ASGO: Adaptive Structured Gradient Optimization
Mar 26, 2025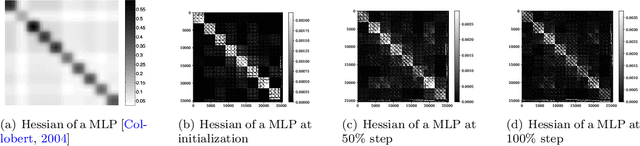

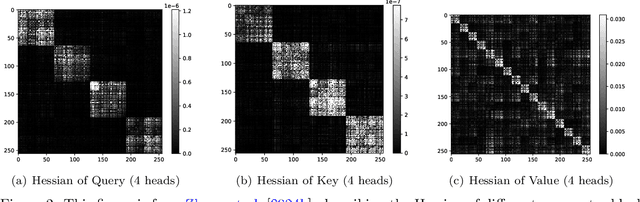
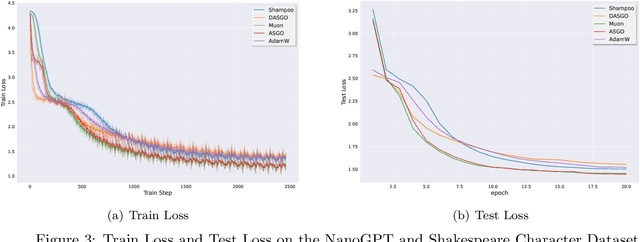
Abstract:Training deep neural networks (DNNs) is a structured optimization problem, because the parameters are naturally represented by matrices and tensors rather than simple vectors. Under this structural representation, it has been widely observed that gradients are low-rank and Hessians are approximately block-wise diagonal. These structured properties are crucial for designing efficient optimization algorithms but may not be utilized by current popular optimizers like Adam. In this paper, we present a novel optimization algorithm ASGO that capitalizes on these properties by employing a preconditioner that is adaptively updated using structured gradients. By fine-grained theoretical analysis, ASGO is proven to achieve superior convergence rates compared to existing structured gradient methods. Based on the convergence theory, we further demonstrate that ASGO can benefit from the low-rank and block-wise diagonal properties. We also discuss practical modifications of ASGO and empirically verify the effectiveness of the algorithm on language model tasks.
Layer-wise Adaptive Step-Sizes for Stochastic First-Order Methods for Deep Learning
May 23, 2023



Abstract:We propose a new per-layer adaptive step-size procedure for stochastic first-order optimization methods for minimizing empirical loss functions in deep learning, eliminating the need for the user to tune the learning rate (LR). The proposed approach exploits the layer-wise stochastic curvature information contained in the diagonal blocks of the Hessian in deep neural networks (DNNs) to compute adaptive step-sizes (i.e., LRs) for each layer. The method has memory requirements that are comparable to those of first-order methods, while its per-iteration time complexity is only increased by an amount that is roughly equivalent to an additional gradient computation. Numerical experiments show that SGD with momentum and AdamW combined with the proposed per-layer step-sizes are able to choose effective LR schedules and outperform fine-tuned LR versions of these methods as well as popular first-order and second-order algorithms for training DNNs on Autoencoder, Convolutional Neural Network (CNN) and Graph Convolutional Network (GCN) models. Finally, it is proved that an idealized version of SGD with the layer-wise step sizes converges linearly when using full-batch gradients.
A Mini-Block Natural Gradient Method for Deep Neural Networks
Feb 16, 2022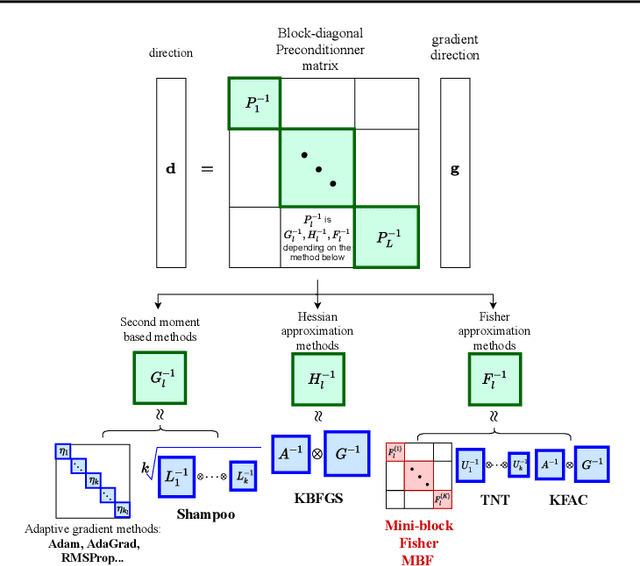
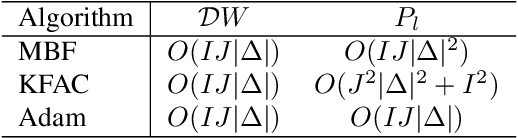
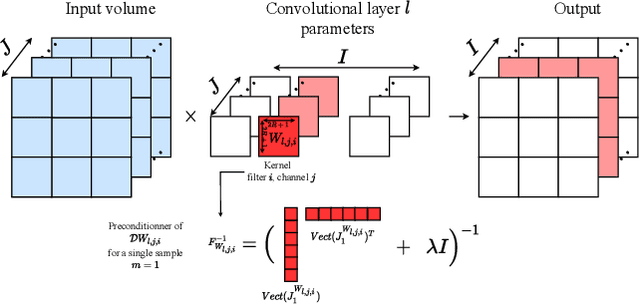

Abstract:The training of deep neural networks (DNNs) is currently predominantly done using first-order methods. Some of these methods (e.g., Adam, AdaGrad, and RMSprop, and their variants) incorporate a small amount of curvature information by using a diagonal matrix to precondition the stochastic gradient. Recently, effective second-order methods, such as KFAC, K-BFGS, Shampoo, and TNT, have been developed for training DNNs, by preconditioning the stochastic gradient by layer-wise block-diagonal matrices. Here we propose and analyze the convergence of an approximate natural gradient method, mini-block Fisher (MBF), that lies in between these two classes of methods. Specifically, our method uses a block-diagonal approximation to the Fisher matrix, where for each layer in the DNN, whether it is convolutional or feed-forward and fully connected, the associated diagonal block is also block-diagonal and is composed of a large number of mini-blocks of modest size. Our novel approach utilizes the parallelism of GPUs to efficiently perform computations on the large number of matrices in each layer. Consequently, MBF's per-iteration computational cost is only slightly higher than it is for first-order methods. Finally, the performance of our proposed method is compared to that of several baseline methods, on both Auto-encoder and CNN problems, to validate its effectiveness both in terms of time efficiency and generalization power.
Tensor Normal Training for Deep Learning Models
Jun 05, 2021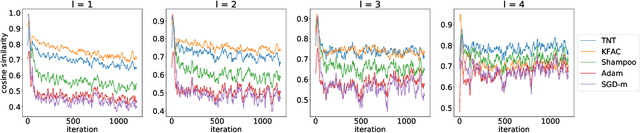

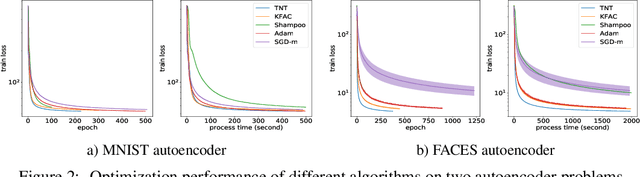
Abstract:Despite the predominant use of first-order methods for training deep learning models, second-order methods, and in particular, natural gradient methods, remain of interest because of their potential for accelerating training through the use of curvature information. Several methods with non-diagonal preconditioning matrices, including KFAC and Shampoo, have been proposed and shown to be effective. Based on the so-called tensor normal (TN) distribution, we propose and analyze a brand new approximate natural gradient method, Tensor Normal Training (TNT), which like Shampoo, only requires knowledge on the shape of the training parameters. By approximating the probabilistically based Fisher matrix, as opposed to the empirical Fisher matrix, our method uses the layer-wise covariance of the sampling based gradient as the pre-conditioning matrix. Moreover, the assumption that the sampling-based (tensor) gradient follows a TN distribution, ensures that its covariance has a Kronecker separable structure, which leads to a tractable approximation to the Fisher matrix. Consequently, TNT's memory requirements and per-iteration computational costs are only slightly higher than those for first-order methods. In our experiments, TNT exhibited superior optimization performance to KFAC and Shampoo, and to state-of-the-art first-order methods. Moreover, TNT demonstrated its ability to generalize as well as these first-order methods, using fewer epochs.
Kronecker-factored Quasi-Newton Methods for Convolutional Neural Networks
Feb 12, 2021

Abstract:Second-order methods have the capability of accelerating optimization by using much richer curvature information than first-order methods. However, most are impractical in a deep learning setting where the number of training parameters is huge. In this paper, we propose KF-QN-CNN, a new Kronecker-factored quasi-Newton method for training convolutional neural networks (CNNs), where the Hessian is approximated by a layer-wise block diagonal matrix and each layer's diagonal block is further approximated by a Kronecker product corresponding to the structure of the Hessian restricted to that layer. New damping and Hessian-action techniques for BFGS are designed to deal with the non-convexity and the particularly large size of Kronecker matrices in CNN models and convergence results are proved for a variant of KF-QN-CNN under relatively mild conditions. KF-QN-CNN has memory requirements comparable to first-order methods and much less per-iteration time complexity than traditional second-order methods. Compared with state-of-the-art first- and second-order methods on several CNN models, KF-QN-CNN consistently exhibited superior performance in all of our tests.
Practical Quasi-Newton Methods for Training Deep Neural Networks
Jun 16, 2020
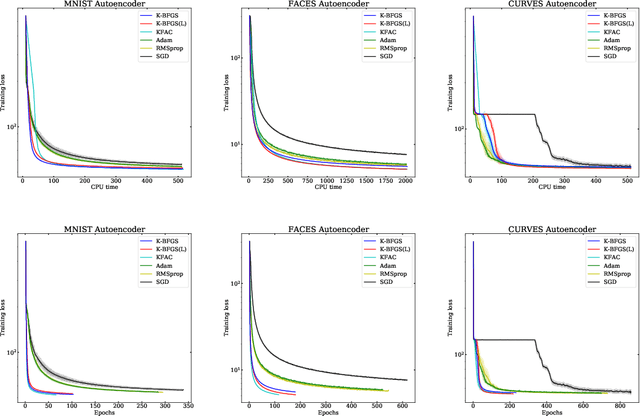

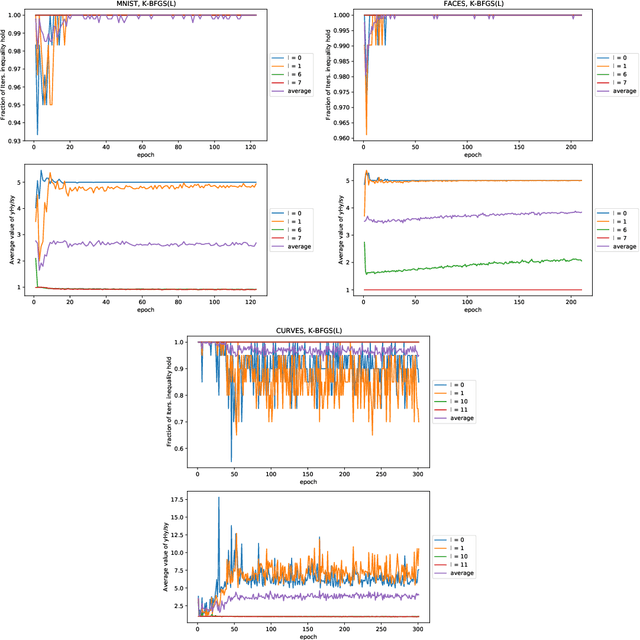
Abstract:We consider the development of practical stochastic quasi-Newton, and in particular Kronecker-factored block-diagonal BFGS and L-BFGS methods, for training deep neural networks (DNNs). In DNN training, the number of variables and components of the gradient $n$ is often of the order of tens of millions and the Hessian has $n^2$ elements. Consequently, computing and storing a full $n \times n$ BFGS approximation or storing a modest number of (step, change in gradient) vector pairs for use in an L-BFGS implementation is out of the question. In our proposed methods, we approximate the Hessian by a block-diagonal matrix and use the structure of the gradient and Hessian to further approximate these blocks, each of which corresponds to a layer, as the Kronecker product of two much smaller matrices. This is analogous to the approach in KFAC, which computes a Kronecker-factored block-diagonal approximation to the Fisher matrix in a stochastic natural gradient method. Because the indefinite and highly variable nature of the Hessian in a DNN, we also propose a new damping approach to keep the upper as well as the lower bounds of the BFGS and L-BFGS approximations bounded. In tests on autoencoder feed-forward neural network models with either nine or thirteen layers applied to three datasets, our methods outperformed or performed comparably to KFAC and state-of-the-art first-order stochastic methods.
A Dynamic Sampling Adaptive-SGD Method for Machine Learning
Dec 31, 2019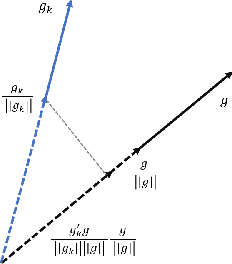
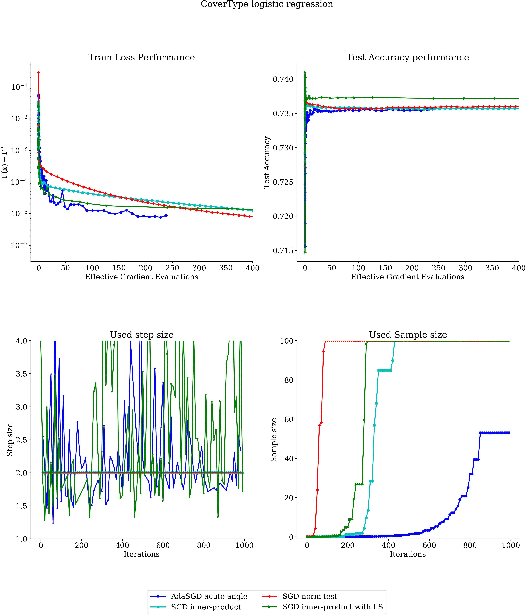
Abstract:We propose a stochastic optimization method for minimizing loss functions, which can be expressed as an expected value, that adaptively controls the batch size used in the computation of gradient approximations and the step size used to move along such directions, eliminating the need for the user to tune the learning rate. The proposed method exploits local curvature information and ensures that search directions are descent directions with high probability using an acute-angle test. The method is proved to have, under reasonable assumptions, a global linear rate of convergence on self-concordant functions with high probability. Numerical experiments show that this method is able to choose the best learning rates and compares favorably to fine-tuned SGD for training logistic regression and Deep Neural Networks (DNNs). We also propose an adaptive version of ADAM that eliminates the need to tune the base learning rate and compares favorably to fine-tuned ADAM for training DNNs.
Efficient Subsampled Gauss-Newton and Natural Gradient Methods for Training Neural Networks
Jun 05, 2019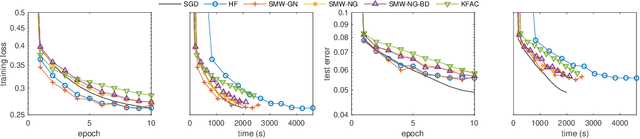
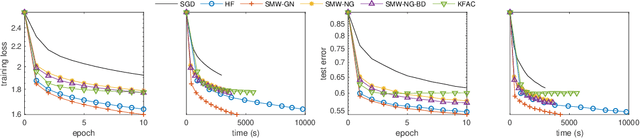
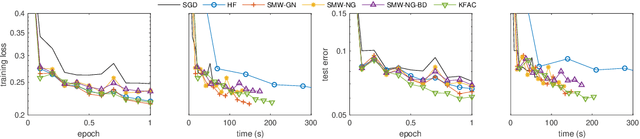
Abstract:We present practical Levenberg-Marquardt variants of Gauss-Newton and natural gradient methods for solving non-convex optimization problems that arise in training deep neural networks involving enormous numbers of variables and huge data sets. Our methods use subsampled Gauss-Newton or Fisher information matrices and either subsampled gradient estimates (fully stochastic) or full gradients (semi-stochastic), which, in the latter case, we prove convergent to a stationary point. By using the Sherman-Morrison-Woodbury formula with automatic differentiation (backpropagation) we show how our methods can be implemented to perform efficiently. Finally, numerical results are presented to demonstrate the effectiveness of our proposed methods.
Leader Stochastic Gradient Descent for Distributed Training of Deep Learning Models
May 24, 2019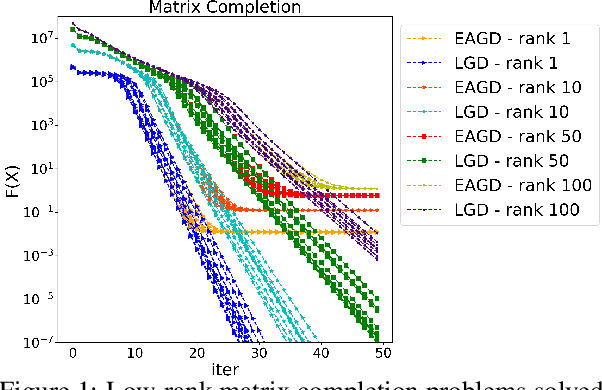
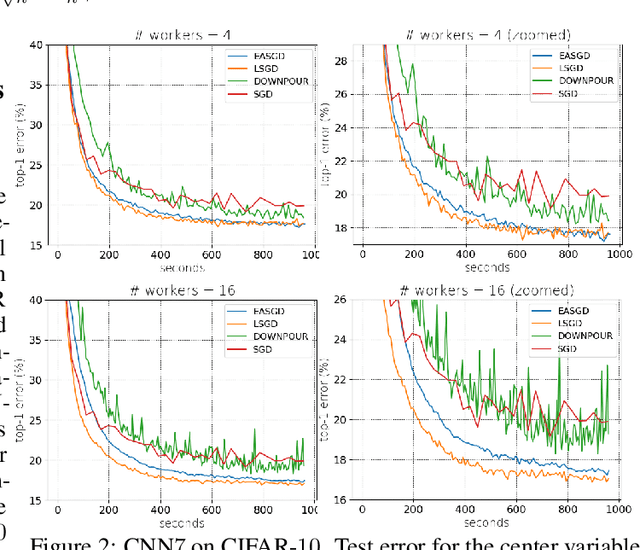


Abstract:We consider distributed optimization under communication constraints for training deep learning models. We propose a new algorithm, whose parameter updates rely on two forces: a regular gradient step, and a corrective direction dictated by the currently best-performing worker (leader). Our method differs from the parameter-averaging scheme EASGD in a number of ways: (i) our objective formulation does not change the location of stationary points compared to the original optimization problem; (ii) we avoid convergence decelerations caused by pulling local workers descending to different local minima to each other (i.e. to the average of their parameters); (iii) our update by design breaks the curse of symmetry (the phenomenon of being trapped in poorly generalizing sub-optimal solutions in symmetric non-convex landscapes); and (iv) our approach is more communication efficient since it broadcasts only parameters of the leader rather than all workers. We provide theoretical analysis of the batch version of the proposed algorithm, which we call Leader Gradient Descent (LGD), and its stochastic variant (LSGD). Finally, we implement an asynchronous version of our algorithm and extend it to the multi-leader setting, where we form groups of workers, each represented by its own local leader (the best performer in a group), and update each worker with a corrective direction comprised of two attractive forces: one to the local, and one to the global leader (the best performer among all workers). The multi-leader setting is well-aligned with current hardware architecture, where local workers forming a group lie within a single computational node and different groups correspond to different nodes. For training convolutional neural networks, we empirically demonstrate that our approach compares favorably to state-of-the-art baselines.
Scalable Robust Matrix Recovery: Frank-Wolfe Meets Proximal Methods
May 29, 2017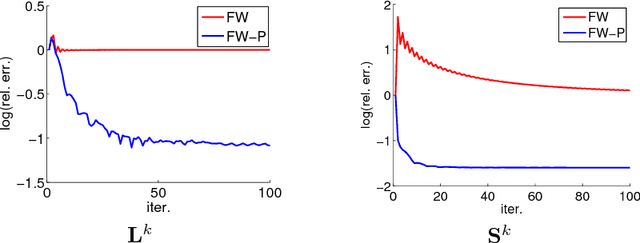
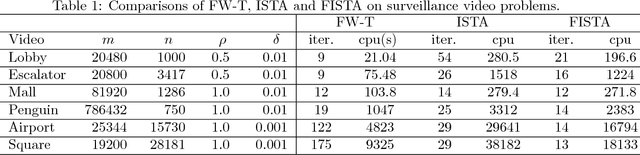
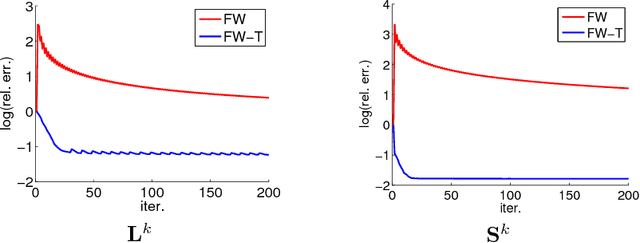
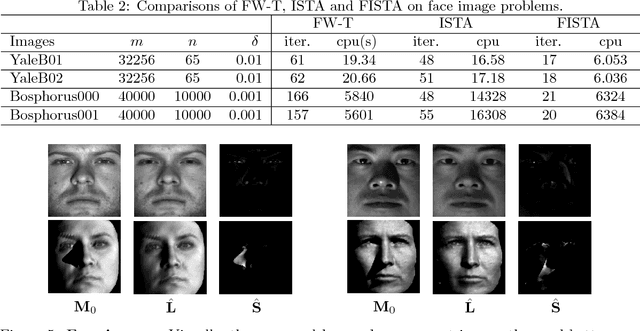
Abstract:Recovering matrices from compressive and grossly corrupted observations is a fundamental problem in robust statistics, with rich applications in computer vision and machine learning. In theory, under certain conditions, this problem can be solved in polynomial time via a natural convex relaxation, known as Compressive Principal Component Pursuit (CPCP). However, all existing provable algorithms for CPCP suffer from superlinear per-iteration cost, which severely limits their applicability to large scale problems. In this paper, we propose provable, scalable and efficient methods to solve CPCP with (essentially) linear per-iteration cost. Our method combines classical ideas from Frank-Wolfe and proximal methods. In each iteration, we mainly exploit Frank-Wolfe to update the low-rank component with rank-one SVD and exploit the proximal step for the sparse term. Convergence results and implementation details are also discussed. We demonstrate the scalability of the proposed approach with promising numerical experiments on visual data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge