A Dynamic Sampling Adaptive-SGD Method for Machine Learning

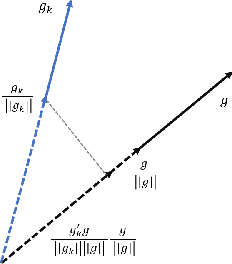
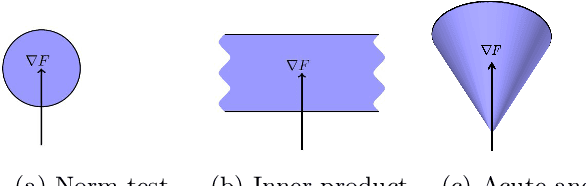
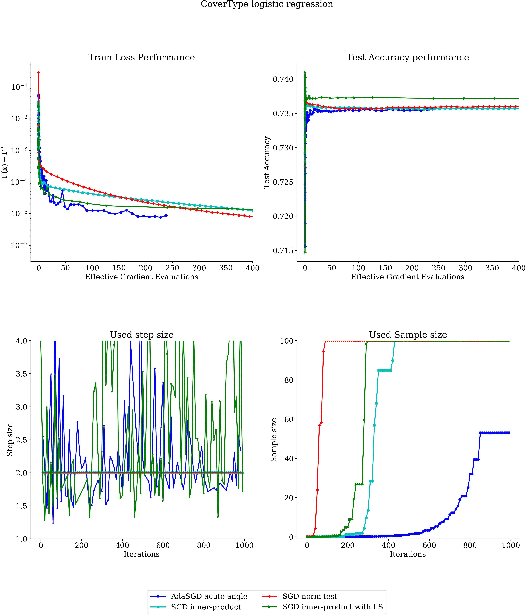
We propose a stochastic optimization method for minimizing loss functions, which can be expressed as an expected value, that adaptively controls the batch size used in the computation of gradient approximations and the step size used to move along such directions, eliminating the need for the user to tune the learning rate. The proposed method exploits local curvature information and ensures that search directions are descent directions with high probability using an acute-angle test. The method is proved to have, under reasonable assumptions, a global linear rate of convergence on self-concordant functions with high probability. Numerical experiments show that this method is able to choose the best learning rates and compares favorably to fine-tuned SGD for training logistic regression and Deep Neural Networks (DNNs). We also propose an adaptive version of ADAM that eliminates the need to tune the base learning rate and compares favorably to fine-tuned ADAM for training DNNs.