Practical Quasi-Newton Methods for Training Deep Neural Networks
Paper and Code
Jun 16, 2020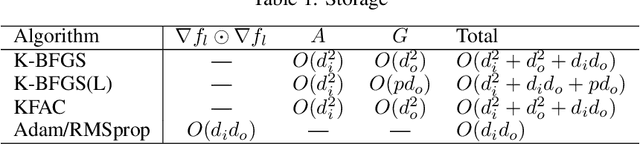
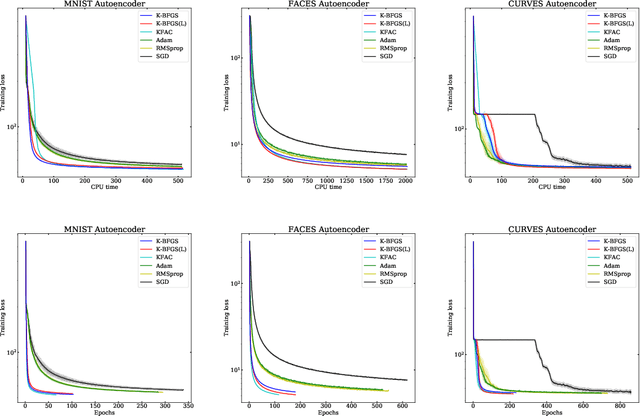

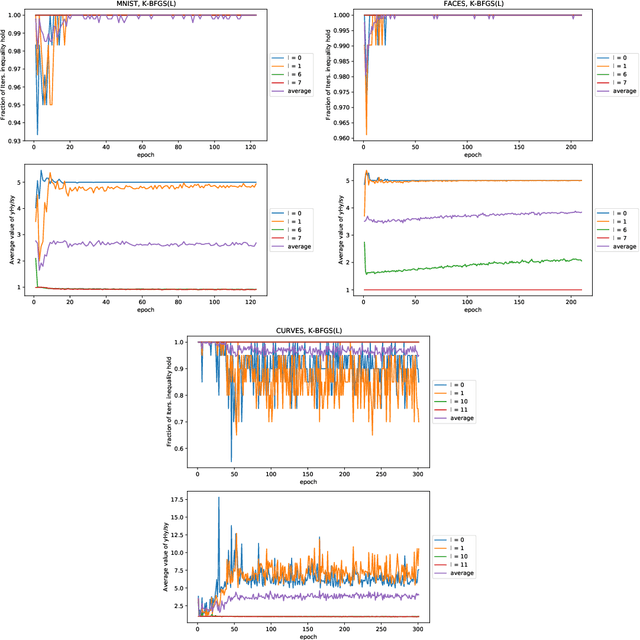
We consider the development of practical stochastic quasi-Newton, and in particular Kronecker-factored block-diagonal BFGS and L-BFGS methods, for training deep neural networks (DNNs). In DNN training, the number of variables and components of the gradient $n$ is often of the order of tens of millions and the Hessian has $n^2$ elements. Consequently, computing and storing a full $n \times n$ BFGS approximation or storing a modest number of (step, change in gradient) vector pairs for use in an L-BFGS implementation is out of the question. In our proposed methods, we approximate the Hessian by a block-diagonal matrix and use the structure of the gradient and Hessian to further approximate these blocks, each of which corresponds to a layer, as the Kronecker product of two much smaller matrices. This is analogous to the approach in KFAC, which computes a Kronecker-factored block-diagonal approximation to the Fisher matrix in a stochastic natural gradient method. Because the indefinite and highly variable nature of the Hessian in a DNN, we also propose a new damping approach to keep the upper as well as the lower bounds of the BFGS and L-BFGS approximations bounded. In tests on autoencoder feed-forward neural network models with either nine or thirteen layers applied to three datasets, our methods outperformed or performed comparably to KFAC and state-of-the-art first-order stochastic methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge