Kronecker-factored Quasi-Newton Methods for Convolutional Neural Networks

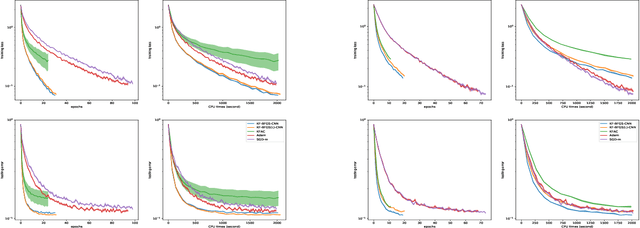
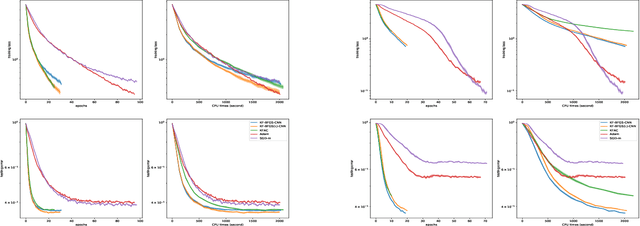
Second-order methods have the capability of accelerating optimization by using much richer curvature information than first-order methods. However, most are impractical in a deep learning setting where the number of training parameters is huge. In this paper, we propose KF-QN-CNN, a new Kronecker-factored quasi-Newton method for training convolutional neural networks (CNNs), where the Hessian is approximated by a layer-wise block diagonal matrix and each layer's diagonal block is further approximated by a Kronecker product corresponding to the structure of the Hessian restricted to that layer. New damping and Hessian-action techniques for BFGS are designed to deal with the non-convexity and the particularly large size of Kronecker matrices in CNN models and convergence results are proved for a variant of KF-QN-CNN under relatively mild conditions. KF-QN-CNN has memory requirements comparable to first-order methods and much less per-iteration time complexity than traditional second-order methods. Compared with state-of-the-art first- and second-order methods on several CNN models, KF-QN-CNN consistently exhibited superior performance in all of our tests.