Efficient Subsampled Gauss-Newton and Natural Gradient Methods for Training Neural Networks
Paper and Code
Jun 05, 2019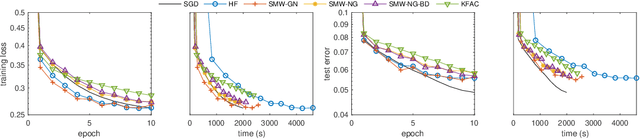
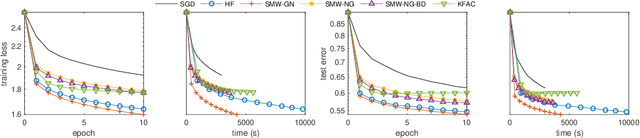
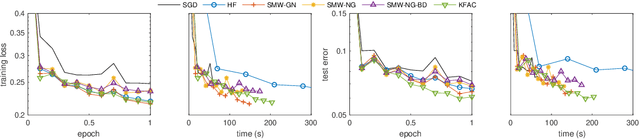
We present practical Levenberg-Marquardt variants of Gauss-Newton and natural gradient methods for solving non-convex optimization problems that arise in training deep neural networks involving enormous numbers of variables and huge data sets. Our methods use subsampled Gauss-Newton or Fisher information matrices and either subsampled gradient estimates (fully stochastic) or full gradients (semi-stochastic), which, in the latter case, we prove convergent to a stationary point. By using the Sherman-Morrison-Woodbury formula with automatic differentiation (backpropagation) we show how our methods can be implemented to perform efficiently. Finally, numerical results are presented to demonstrate the effectiveness of our proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge