Strongly Consistent Community Detection in Popularity Adjusted Block Models

The Popularity Adjusted Block Model (PABM) provides a flexible framework for community detection in network data by allowing heterogeneous node popularity across communities. However, this flexibility increases model complexity and raises key unresolved challenges, particularly in effectively adapting spectral clustering techniques and efficiently achieving strong consistency in label recovery. To address these challenges, we first propose the Thresholded Cosine Spectral Clustering (TCSC) algorithm and establish its weak consistency under the PABM. We then introduce the one-step Refined TCSC algorithm and prove that it achieves strong consistency under the PABM, correctly recovering all community labels with high probability. We further show that the two-step Refined TCSC accelerates clustering error convergence, especially with small sample sizes. Additionally, we propose a data-driven approach for selecting the number of communities, which outperforms existing methods under the PABM. The effectiveness and robustness of our methods are validated through extensive simulations and real-world applications.

Regret-Optimal Q-Learning with Low Cost for Single-Agent and Federated Reinforcement Learning

Motivated by real-world settings where data collection and policy deployment -- whether for a single agent or across multiple agents -- are costly, we study the problem of on-policy single-agent reinforcement learning (RL) and federated RL (FRL) with a focus on minimizing burn-in costs (the sample sizes needed to reach near-optimal regret) and policy switching or communication costs. In parallel finite-horizon episodic Markov Decision Processes (MDPs) with $S$ states and $A$ actions, existing methods either require superlinear burn-in costs in $S$ and $A$ or fail to achieve logarithmic switching or communication costs. We propose two novel model-free RL algorithms -- Q-EarlySettled-LowCost and FedQ-EarlySettled-LowCost -- that are the first in the literature to simultaneously achieve: (i) the best near-optimal regret among all known model-free RL or FRL algorithms, (ii) low burn-in cost that scales linearly with $S$ and $A$, and (iii) logarithmic policy switching cost for single-agent RL or communication cost for FRL. Additionally, we establish gap-dependent theoretical guarantees for both regret and switching/communication costs, improving or matching the best-known gap-dependent bounds.

AltLoRA: Towards Better Gradient Approximation in Low-Rank Adaptation with Alternating Projections

Low-Rank Adaptation (LoRA) has emerged as an effective technique for reducing memory overhead in fine-tuning large language models. However, it often suffers from sub-optimal performance compared with full fine-tuning since the update is constrained in the low-rank space. Recent variants such as LoRA-Pro attempt to mitigate this by adjusting the gradients of the low-rank matrices to approximate the full gradient. However, LoRA-Pro's solution is not unique, and different solutions can lead to significantly varying performance in ablation studies. Besides, to incorporate momentum or adaptive optimization design, approaches like LoRA-Pro must first compute the equivalent gradient, causing a higher memory cost close to full fine-tuning. A key challenge remains in integrating momentum properly into the low-rank space with lower memory cost. In this work, we propose AltLoRA, an alternating projection method that avoids the difficulties in gradient approximation brought by the joint update design, meanwhile integrating momentum without higher memory complexity. Our theoretical analysis provides convergence guarantees and further shows that AltLoRA enables stable feature learning and robustness to transformation invariance. Extensive experiments across multiple tasks demonstrate that AltLoRA outperforms LoRA and its variants, narrowing the gap toward full fine-tuning while preserving superior memory efficiency.

Gap-Dependent Bounds for Federated $Q$-learning

We present the first gap-dependent analysis of regret and communication cost for on-policy federated $Q$-Learning in tabular episodic finite-horizon Markov decision processes (MDPs). Existing FRL methods focus on worst-case scenarios, leading to $\sqrt{T}$-type regret bounds and communication cost bounds with a $\log T$ term scaling with the number of agents $M$, states $S$, and actions $A$, where $T$ is the average total number of steps per agent. In contrast, our novel framework leverages the benign structures of MDPs, such as a strictly positive suboptimality gap, to achieve a $\log T$-type regret bound and a refined communication cost bound that disentangles exploration and exploitation. Our gap-dependent regret bound reveals a distinct multi-agent speedup pattern, and our gap-dependent communication cost bound removes the dependence on $MSA$ from the $\log T$ term. Notably, our gap-dependent communication cost bound also yields a better global switching cost when $M=1$, removing $SA$ from the $\log T$ term.

Statistical Convergence Rates of Optimal Transport Map Estimation between General Distributions

This paper studies the convergence rates of optimal transport (OT) map estimators, a topic of growing interest in statistics, machine learning, and various scientific fields. Despite recent advancements, existing results rely on regularity assumptions that are very restrictive in practice and much stricter than those in Brenier's Theorem, including the compactness and convexity of the probability support and the bi-Lipschitz property of the OT maps. We aim to broaden the scope of OT map estimation and fill this gap between theory and practice. Given the strong convexity assumption on Brenier's potential, we first establish the non-asymptotic convergence rates for the original plug-in estimator without requiring restrictive assumptions on probability measures. Additionally, we introduce a sieve plug-in estimator and establish its convergence rates without the strong convexity assumption on Brenier's potential, enabling the widely used cases such as the rank functions of normal or t-distributions. We also establish new Poincar\'e-type inequalities, which are proved given sufficient conditions on the local boundedness of the probability density and mild topological conditions of the support, and these new inequalities enable us to achieve faster convergence rates for the Donsker function class. Moreover, we develop scalable algorithms to efficiently solve the OT map estimation using neural networks and present numerical experiments to demonstrate the effectiveness and robustness.

The Effect of Personalization in FedProx: A Fine-grained Analysis on Statistical Accuracy and Communication Efficiency

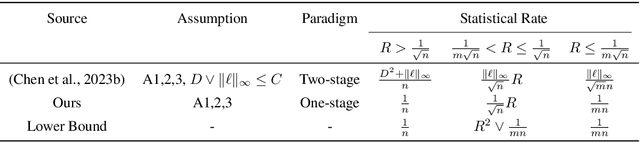
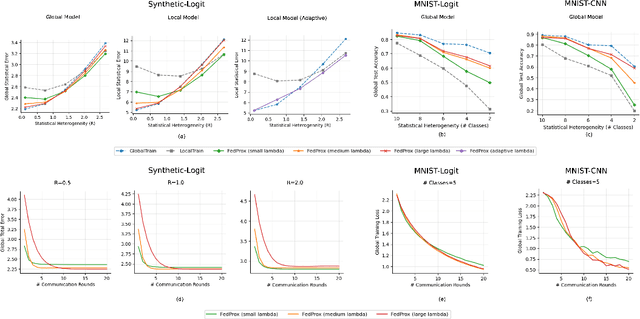
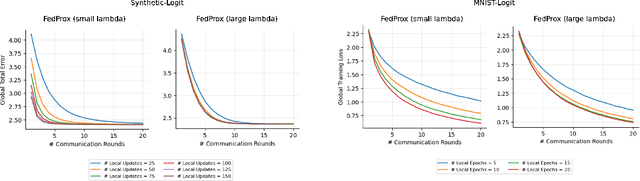
FedProx is a simple yet effective federated learning method that enables model personalization via regularization. Despite remarkable success in practice, a rigorous analysis of how such a regularization provably improves the statistical accuracy of each client's local model hasn't been fully established. Setting the regularization strength heuristically presents a risk, as an inappropriate choice may even degrade accuracy. This work fills in the gap by analyzing the effect of regularization on statistical accuracy, thereby providing a theoretical guideline for setting the regularization strength for achieving personalization. We prove that by adaptively choosing the regularization strength under different statistical heterogeneity, FedProx can consistently outperform pure local training and achieve a nearly minimax-optimal statistical rate. In addition, to shed light on resource allocation, we design an algorithm, provably showing that stronger personalization reduces communication complexity without increasing the computation cost overhead. Finally, our theory is validated on both synthetic and real-world datasets and its generalizability is verified in a non-convex setting.

Gap-Dependent Bounds for Q-Learning using Reference-Advantage Decomposition

We study the gap-dependent bounds of two important algorithms for on-policy Q-learning for finite-horizon episodic tabular Markov Decision Processes (MDPs): UCB-Advantage (Zhang et al. 2020) and Q-EarlySettled-Advantage (Li et al. 2021). UCB-Advantage and Q-EarlySettled-Advantage improve upon the results based on Hoeffding-type bonuses and achieve the almost optimal $\sqrt{T}$-type regret bound in the worst-case scenario, where $T$ is the total number of steps. However, the benign structures of the MDPs such as a strictly positive suboptimality gap can significantly improve the regret. While gap-dependent regret bounds have been obtained for Q-learning with Hoeffding-type bonuses, it remains an open question to establish gap-dependent regret bounds for Q-learning using variance estimators in their bonuses and reference-advantage decomposition for variance reduction. We develop a novel error decomposition framework to prove gap-dependent regret bounds of UCB-Advantage and Q-EarlySettled-Advantage that are logarithmic in $T$ and improve upon existing ones for Q-learning algorithms. Moreover, we establish the gap-dependent bound for the policy switching cost of UCB-Advantage and improve that under the worst-case MDPs. To our knowledge, this paper presents the first gap-dependent regret analysis for Q-learning using variance estimators and reference-advantage decomposition and also provides the first gap-dependent analysis on policy switching cost for Q-learning.

Smoothed Robust Phase Retrieval

The phase retrieval problem in the presence of noise aims to recover the signal vector of interest from a set of quadratic measurements with infrequent but arbitrary corruptions, and it plays an important role in many scientific applications. However, the essential geometric structure of the nonconvex robust phase retrieval based on the $\ell_1$-loss is largely unknown to study spurious local solutions, even under the ideal noiseless setting, and its intrinsic nonsmooth nature also impacts the efficiency of optimization algorithms. This paper introduces the smoothed robust phase retrieval (SRPR) based on a family of convolution-type smoothed loss functions. Theoretically, we prove that the SRPR enjoys a benign geometric structure with high probability: (1) under the noiseless situation, the SRPR has no spurious local solutions, and the target signals are global solutions, and (2) under the infrequent but arbitrary corruptions, we characterize the stationary points of the SRPR and prove its benign landscape, which is the first landscape analysis of phase retrieval with corruption in the literature. Moreover, we prove the local linear convergence rate of gradient descent for solving the SRPR under the noiseless situation. Experiments on both simulated datasets and image recovery are provided to demonstrate the numerical performance of the SRPR.

Federated Q-Learning with Reference-Advantage Decomposition: Almost Optimal Regret and Logarithmic Communication Cost

In this paper, we consider model-free federated reinforcement learning for tabular episodic Markov decision processes. Under the coordination of a central server, multiple agents collaboratively explore the environment and learn an optimal policy without sharing their raw data. Despite recent advances in federated Q-learning algorithms achieving near-linear regret speedup with low communication cost, existing algorithms only attain suboptimal regrets compared to the information bound. We propose a novel model-free federated Q-learning algorithm, termed FedQ-Advantage. Our algorithm leverages reference-advantage decomposition for variance reduction and operates under two distinct mechanisms: synchronization between the agents and the server, and policy update, both triggered by events. We prove that our algorithm not only requires a lower logarithmic communication cost but also achieves an almost optimal regret, reaching the information bound up to a logarithmic factor and near-linear regret speedup compared to its single-agent counterpart when the time horizon is sufficiently large.

A Unified Combination Framework for Dependent Tests with Applications to Microbiome Association Studies

We introduce a novel meta-analysis framework to combine dependent tests under a general setting, and utilize it to synthesize various microbiome association tests that are calculated from the same dataset. Our development builds upon the classical meta-analysis methods of aggregating $p$-values and also a more recent general method of combining confidence distributions, but makes generalizations to handle dependent tests. The proposed framework ensures rigorous statistical guarantees, and we provide a comprehensive study and compare it with various existing dependent combination methods. Notably, we demonstrate that the widely used Cauchy combination method for dependent tests, referred to as the vanilla Cauchy combination in this article, can be viewed as a special case within our framework. Moreover, the proposed framework provides a way to address the problem when the distributional assumptions underlying the vanilla Cauchy combination are violated. Our numerical results demonstrate that ignoring the dependence among the to-be-combined components may lead to a severe size distortion phenomenon. Compared to the existing $p$-value combination methods, including the vanilla Cauchy combination method, the proposed combination framework can handle the dependence accurately and utilizes the information efficiently to construct tests with accurate size and enhanced power. The development is applied to Microbiome Association Studies, where we aggregate information from multiple existing tests using the same dataset. The combined tests harness the strengths of each individual test across a wide range of alternative spaces, %resulting in a significant enhancement of testing power across a wide range of alternative spaces, enabling more efficient and meaningful discoveries of vital microbiome associations.