KMM: Key Frame Mask Mamba for Extended Motion Generation

Human motion generation is a cut-edge area of research in generative computer vision, with promising applications in video creation, game development, and robotic manipulation. The recent Mamba architecture shows promising results in efficiently modeling long and complex sequences, yet two significant challenges remain: Firstly, directly applying Mamba to extended motion generation is ineffective, as the limited capacity of the implicit memory leads to memory decay. Secondly, Mamba struggles with multimodal fusion compared to Transformers, and lack alignment with textual queries, often confusing directions (left or right) or omitting parts of longer text queries. To address these challenges, our paper presents three key contributions: Firstly, we introduce KMM, a novel architecture featuring Key frame Masking Modeling, designed to enhance Mamba's focus on key actions in motion segments. This approach addresses the memory decay problem and represents a pioneering method in customizing strategic frame-level masking in SSMs. Additionally, we designed a contrastive learning paradigm for addressing the multimodal fusion problem in Mamba and improving the motion-text alignment. Finally, we conducted extensive experiments on the go-to dataset, BABEL, achieving state-of-the-art performance with a reduction of more than 57% in FID and 70% parameters compared to previous state-of-the-art methods. See project website: https://steve-zeyu-zhang.github.io/KMM

Fisher's combined probability test for high-dimensional covariance matrices

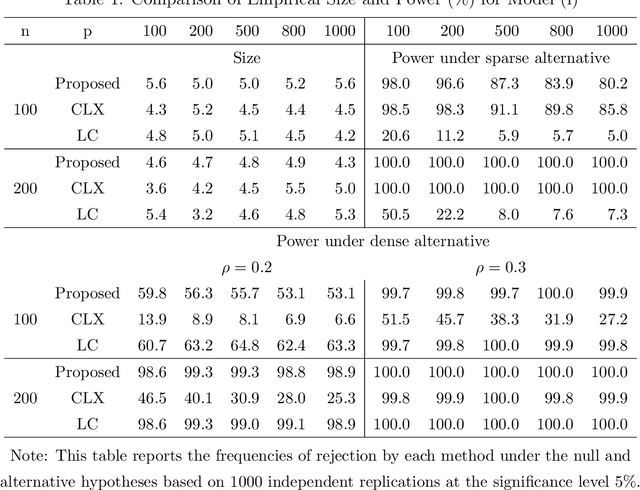
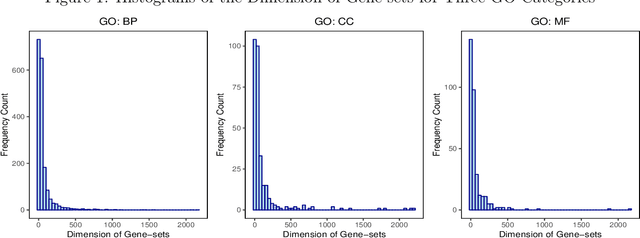
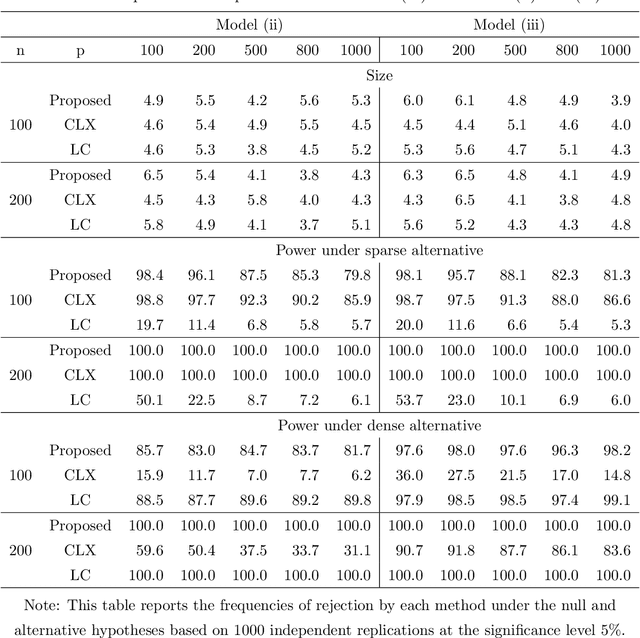
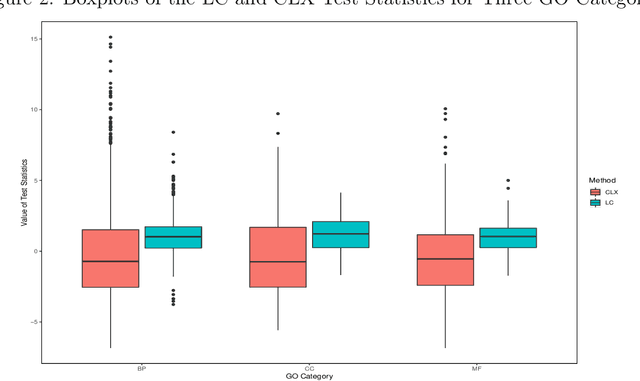
Testing large covariance matrices is of fundamental importance in statistical analysis with high-dimensional data. In the past decade, three types of test statistics have been studied in the literature: quadratic form statistics, maximum form statistics, and their weighted combination. It is known that quadratic form statistics would suffer from low power against sparse alternatives and maximum form statistics would suffer from low power against dense alternatives. The weighted combination methods were introduced to enhance the power of quadratic form statistics or maximum form statistics when the weights are appropriately chosen. In this paper, we provide a new perspective to exploit the full potential of quadratic form statistics and maximum form statistics for testing high-dimensional covariance matrices. We propose a scale-invariant power enhancement test based on Fisher's method to combine the p-values of quadratic form statistics and maximum form statistics. After carefully studying the asymptotic joint distribution of quadratic form statistics and maximum form statistics, we prove that the proposed combination method retains the correct asymptotic size and boosts the power against more general alternatives. Moreover, we demonstrate the finite-sample performance in simulation studies and a real application.

Joint limiting laws for high-dimensional independence tests

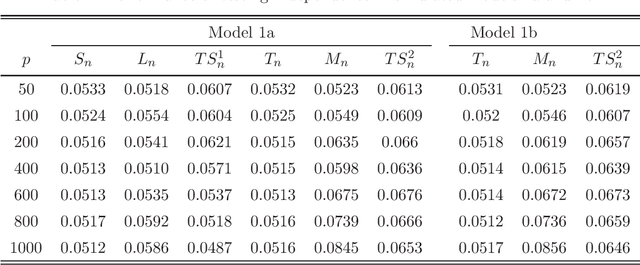
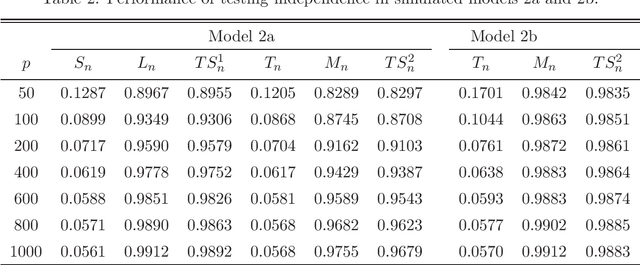
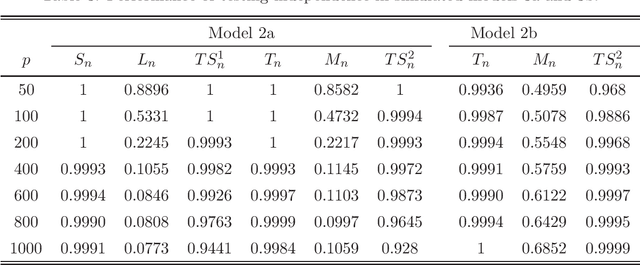
Testing independence is of significant interest in many important areas of large-scale inference. Using extreme-value form statistics to test against sparse alternatives and using quadratic form statistics to test against dense alternatives are two important testing procedures for high-dimensional independence. However, quadratic form statistics suffer from low power against sparse alternatives, and extreme-value form statistics suffer from low power against dense alternatives with small disturbances and may have size distortions due to its slow convergence. For real-world applications, it is important to derive powerful testing procedures against more general alternatives. Based on intermediate limiting distributions, we derive (model-free) joint limiting laws of extreme-value form and quadratic form statistics, and surprisingly, we prove that they are asymptotically independent. Given such asymptotic independencies, we propose (model-free) testing procedures to boost the power against general alternatives and also retain the correct asymptotic size. Under the high-dimensional setting, we derive the closed-form limiting null distributions, and obtain their explicit rates of uniform convergence. We prove their consistent statistical powers against general alternatives. We demonstrate the performance of our proposed test statistics in simulation studies. Our work provides very helpful insights to high-dimensional independence tests, and fills an important gap.