Learning Long Short-Term Intention within Human Daily Behaviors

In the domain of autonomous household robots, it is of utmost importance for robots to understand human behaviors and provide appropriate services. This requires the robots to possess the capability to analyze complex human behaviors and predict the true intentions of humans. Traditionally, humans are perceived as flawless, with their decisions acting as the standards that robots should strive to align with. However, this raises a pertinent question: What if humans make mistakes? In this research, we present a unique task, termed "long short-term intention prediction". This task requires robots can predict the long-term intention of humans, which aligns with human values, and the short term intention of humans, which reflects the immediate action intention. Meanwhile, the robots need to detect the potential non-consistency between the short-term and long-term intentions, and provide necessary warnings and suggestions. To facilitate this task, we propose a long short-term intention model to represent the complex intention states, and build a dataset to train this intention model. Then we propose a two-stage method to integrate the intention model for robots: i) predicting human intentions of both value-based long-term intentions and action-based short-term intentions; and 2) analyzing the consistency between the long-term and short-term intentions. Experimental results indicate that the proposed long short-term intention model can assist robots in comprehending human behavioral patterns over both long-term and short-term durations, which helps determine the consistency between long-term and short-term intentions of humans.

Infant Cry Detection Using Causal Temporal Representation

This paper addresses a major challenge in acoustic event detection, in particular infant cry detection in the presence of other sounds and background noises: the lack of precise annotated data. We present two contributions for supervised and unsupervised infant cry detection. The first is an annotated dataset for cry segmentation, which enables supervised models to achieve state-of-the-art performance. Additionally, we propose a novel unsupervised method, Causal Representation Spare Transition Clustering (CRSTC), based on causal temporal representation, which helps address the issue of data scarcity more generally. By integrating the detected cry segments, we significantly improve the performance of downstream infant cry classification, highlighting the potential of this approach for infant care applications.

AgFlow: Fast Model Selection of Penalized PCA via Implicit Regularization Effects of Gradient Flow

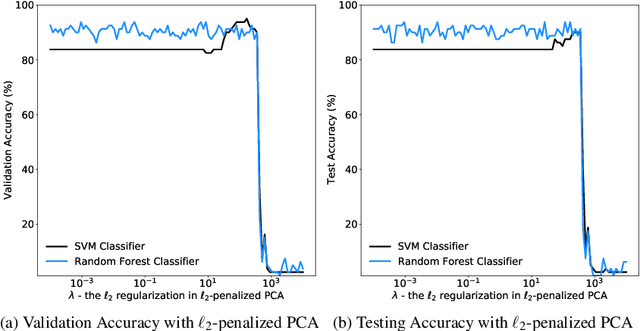
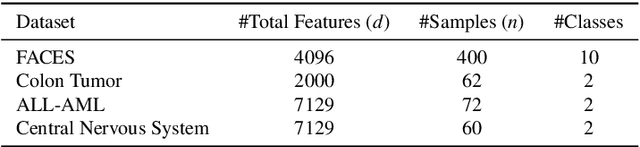
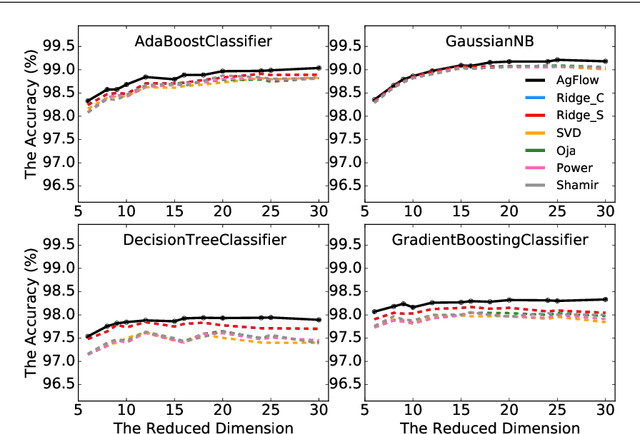
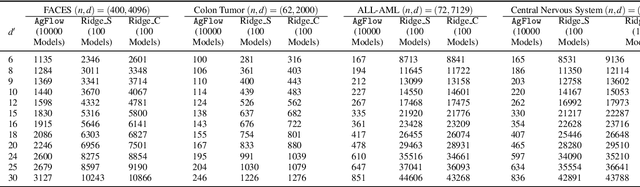
Principal component analysis (PCA) has been widely used as an effective technique for feature extraction and dimension reduction. In the High Dimension Low Sample Size (HDLSS) setting, one may prefer modified principal components, with penalized loadings, and automated penalty selection by implementing model selection among these different models with varying penalties. The earlier work [1, 2] has proposed penalized PCA, indicating the feasibility of model selection in $L_2$- penalized PCA through the solution path of Ridge regression, however, it is extremely time-consuming because of the intensive calculation of matrix inverse. In this paper, we propose a fast model selection method for penalized PCA, named Approximated Gradient Flow (AgFlow), which lowers the computation complexity through incorporating the implicit regularization effect introduced by (stochastic) gradient flow [3, 4] and obtains the complete solution path of $L_2$-penalized PCA under varying $L_2$-regularization. We perform extensive experiments on real-world datasets. AgFlow outperforms existing methods (Oja [5], Power [6], and Shamir [7] and the vanilla Ridge estimators) in terms of computation costs.

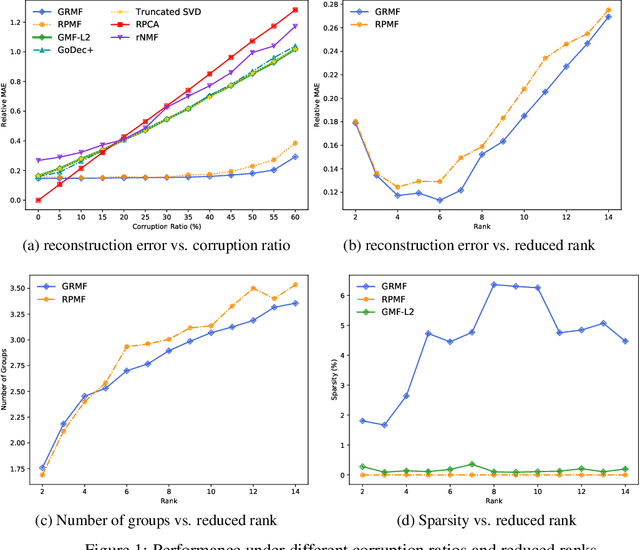
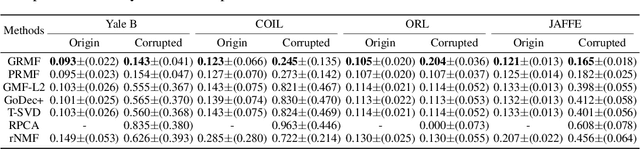
Robust Matrix Factorization with Grouping Effect

Although many techniques have been applied to matrix factorization (MF), they may not fully exploit the feature structure. In this paper, we incorporate the grouping effect into MF and propose a novel method called Robust Matrix Factorization with Grouping effect (GRMF). The grouping effect is a generalization of the sparsity effect, which conducts denoising by clustering similar values around multiple centers instead of just around 0. Compared with existing algorithms, the proposed GRMF can automatically learn the grouping structure and sparsity in MF without prior knowledge, by introducing a naturally adjustable non-convex regularization to achieve simultaneous sparsity and grouping effect. Specifically, GRMF uses an efficient alternating minimization framework to perform MF, in which the original non-convex problem is first converted into a convex problem through Difference-of-Convex (DC) programming, and then solved by Alternating Direction Method of Multipliers (ADMM). In addition, GRMF can be easily extended to the Non-negative Matrix Factorization (NMF) settings. Extensive experiments have been conducted using real-world data sets with outliers and contaminated noise, where the experimental results show that GRMF has promoted performance and robustness, compared to five benchmark algorithms.

Feature Grouping and Sparse Principal Component Analysis

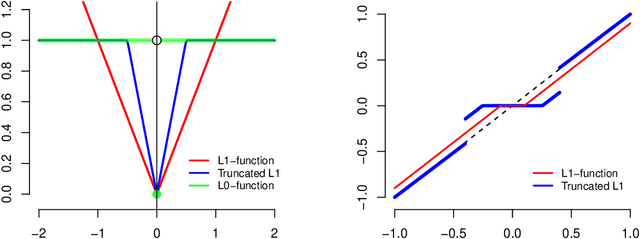
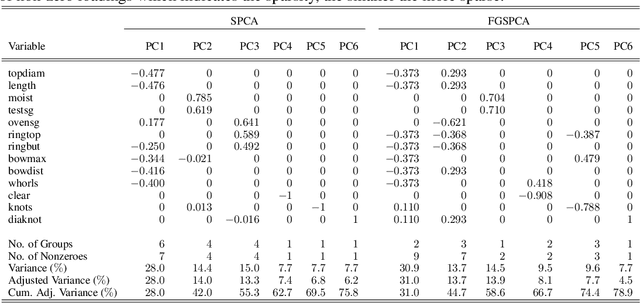
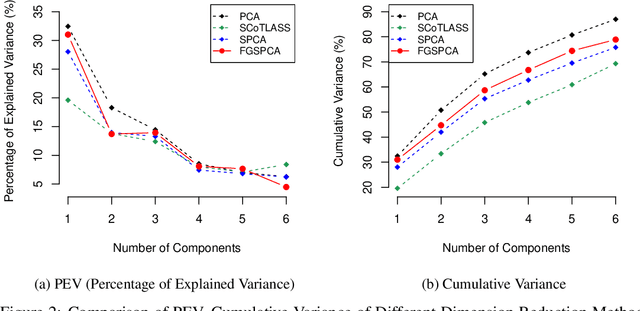
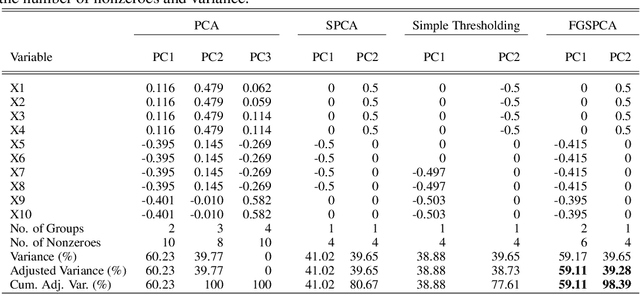
Sparse Principal Component Analysis (SPCA) is widely used in data processing and dimension reduction; it uses the lasso to produce modified principal components with sparse loadings for better interpretability. However, sparse PCA never considers an additional grouping structure where the loadings share similar coefficients (i.e., feature grouping), besides a special group with all coefficients being zero (i.e., feature selection). In this paper, we propose a novel method called Feature Grouping and Sparse Principal Component Analysis (FGSPCA) which allows the loadings to belong to disjoint homogeneous groups, with sparsity as a special case. The proposed FGSPCA is a subspace learning method designed to simultaneously perform grouping pursuit and feature selection, by imposing a non-convex regularization with naturally adjustable sparsity and grouping effect. To solve the resulting non-convex optimization problem, we propose an alternating algorithm that incorporates the difference-of-convex programming, augmented Lagrange and coordinate descent methods. Additionally, the experimental results on real data sets show that the proposed FGSPCA benefits from the grouping effect compared with methods without grouping effect.