Shanshan Qin
Feature Grouping and Sparse Principal Component Analysis
Jun 25, 2021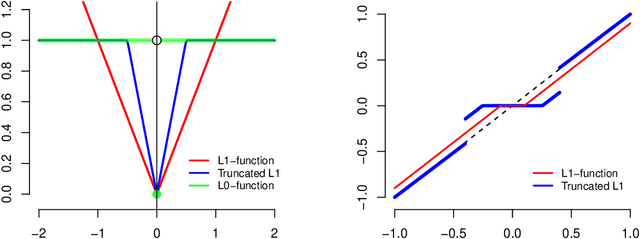
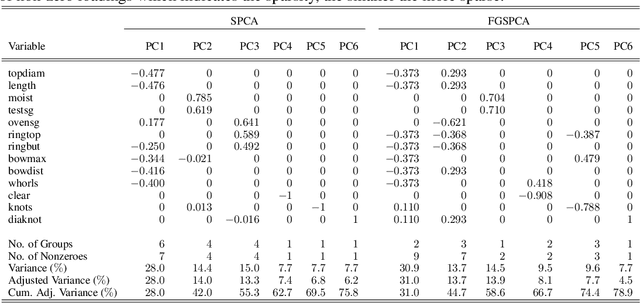
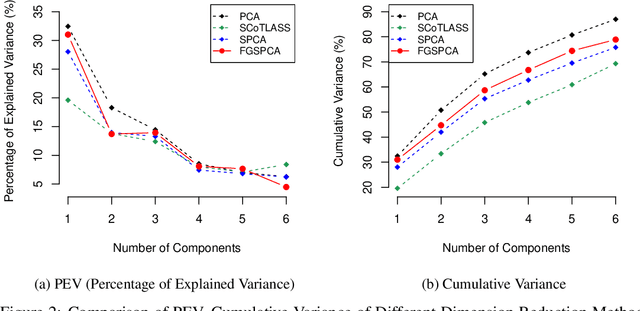
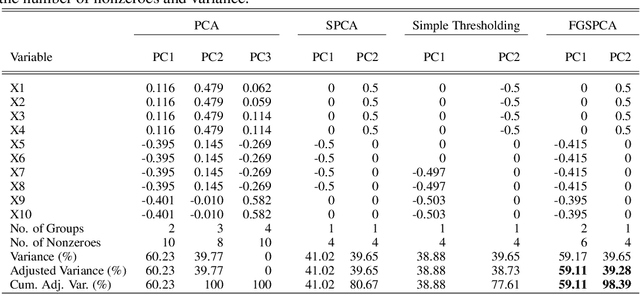
Abstract:Sparse Principal Component Analysis (SPCA) is widely used in data processing and dimension reduction; it uses the lasso to produce modified principal components with sparse loadings for better interpretability. However, sparse PCA never considers an additional grouping structure where the loadings share similar coefficients (i.e., feature grouping), besides a special group with all coefficients being zero (i.e., feature selection). In this paper, we propose a novel method called Feature Grouping and Sparse Principal Component Analysis (FGSPCA) which allows the loadings to belong to disjoint homogeneous groups, with sparsity as a special case. The proposed FGSPCA is a subspace learning method designed to simultaneously perform grouping pursuit and feature selection, by imposing a non-convex regularization with naturally adjustable sparsity and grouping effect. To solve the resulting non-convex optimization problem, we propose an alternating algorithm that incorporates the difference-of-convex programming, augmented Lagrange and coordinate descent methods. Additionally, the experimental results on real data sets show that the proposed FGSPCA benefits from the grouping effect compared with methods without grouping effect.
Supervised Deep Similarity Matching
Mar 10, 2020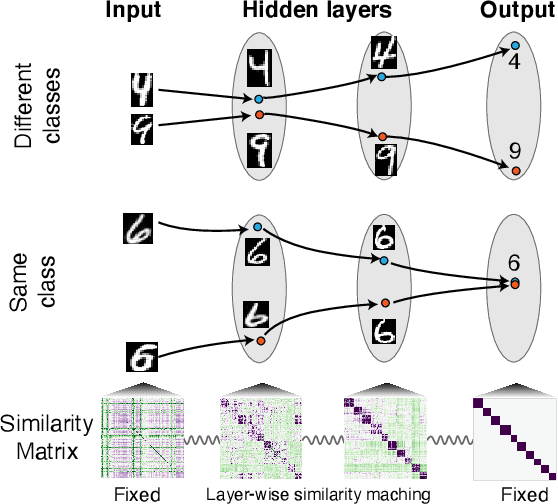

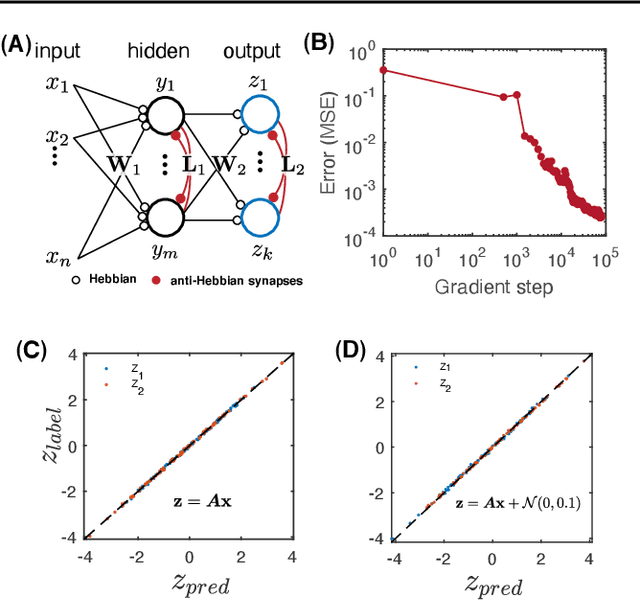
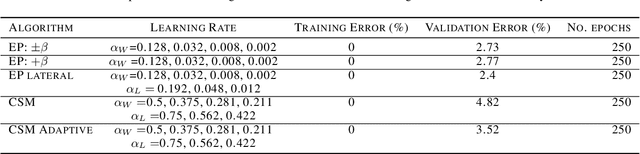
Abstract:We propose a novel biologically-plausible solution to the credit assignment problem, being motivated by observations in the ventral visual pathway and trained deep neural networks. In both, representations of objects in the same category become progressively more similar, while objects belonging to different categories becomes less similar. We use this observation to motivate a layer-specific learning goal in a deep network: each layer aims to learn a representational similarity matrix that interpolates between previous and later layers. We formulate this idea using a supervised deep similarity matching cost function and derive from it deep neural networks with feedforward, lateral and feedback connections, and neurons that exhibit biologically-plausible Hebbian and anti-Hebbian plasticity. Supervised deep similarity matching can be interpreted as an energy-based learning algorithm, but with significant differences from others in how a contrastive function is constructed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge