Joint limiting laws for high-dimensional independence tests
Paper and Code
Dec 30, 2015
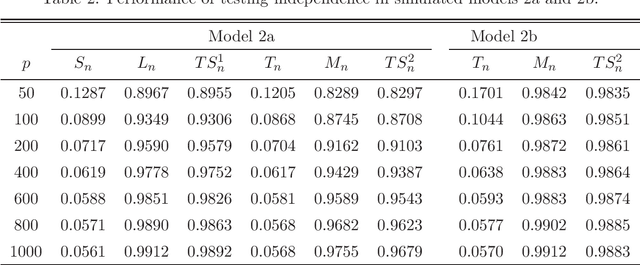
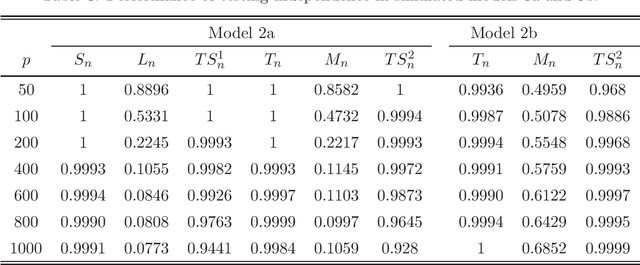
Testing independence is of significant interest in many important areas of large-scale inference. Using extreme-value form statistics to test against sparse alternatives and using quadratic form statistics to test against dense alternatives are two important testing procedures for high-dimensional independence. However, quadratic form statistics suffer from low power against sparse alternatives, and extreme-value form statistics suffer from low power against dense alternatives with small disturbances and may have size distortions due to its slow convergence. For real-world applications, it is important to derive powerful testing procedures against more general alternatives. Based on intermediate limiting distributions, we derive (model-free) joint limiting laws of extreme-value form and quadratic form statistics, and surprisingly, we prove that they are asymptotically independent. Given such asymptotic independencies, we propose (model-free) testing procedures to boost the power against general alternatives and also retain the correct asymptotic size. Under the high-dimensional setting, we derive the closed-form limiting null distributions, and obtain their explicit rates of uniform convergence. We prove their consistent statistical powers against general alternatives. We demonstrate the performance of our proposed test statistics in simulation studies. Our work provides very helpful insights to high-dimensional independence tests, and fills an important gap.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge