Fisher's combined probability test for high-dimensional covariance matrices
Paper and Code
May 31, 2020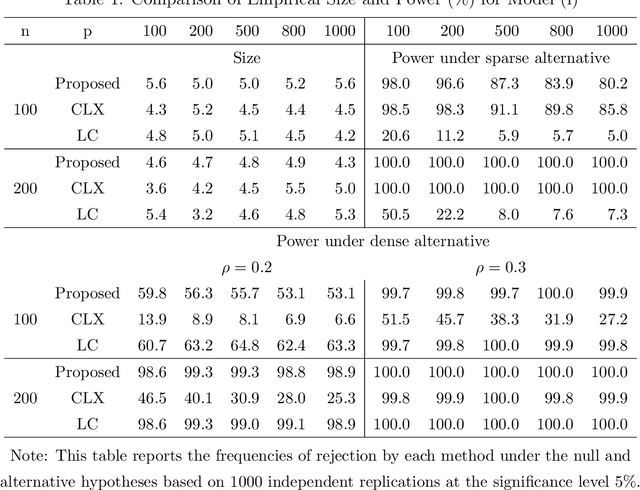
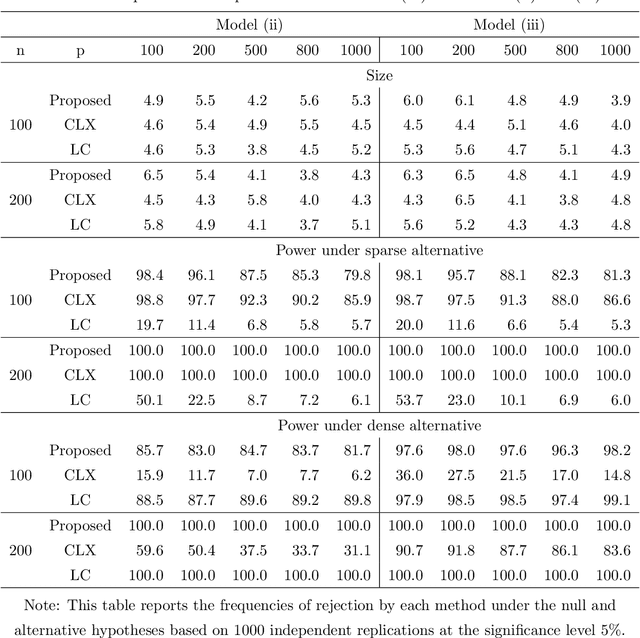
Testing large covariance matrices is of fundamental importance in statistical analysis with high-dimensional data. In the past decade, three types of test statistics have been studied in the literature: quadratic form statistics, maximum form statistics, and their weighted combination. It is known that quadratic form statistics would suffer from low power against sparse alternatives and maximum form statistics would suffer from low power against dense alternatives. The weighted combination methods were introduced to enhance the power of quadratic form statistics or maximum form statistics when the weights are appropriately chosen. In this paper, we provide a new perspective to exploit the full potential of quadratic form statistics and maximum form statistics for testing high-dimensional covariance matrices. We propose a scale-invariant power enhancement test based on Fisher's method to combine the p-values of quadratic form statistics and maximum form statistics. After carefully studying the asymptotic joint distribution of quadratic form statistics and maximum form statistics, we prove that the proposed combination method retains the correct asymptotic size and boosts the power against more general alternatives. Moreover, we demonstrate the finite-sample performance in simulation studies and a real application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge