Pipeline Gradient-based Model Training on Analog In-memory Accelerators

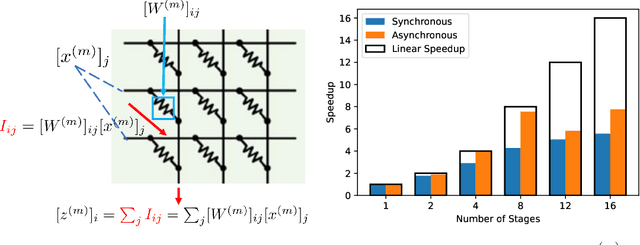
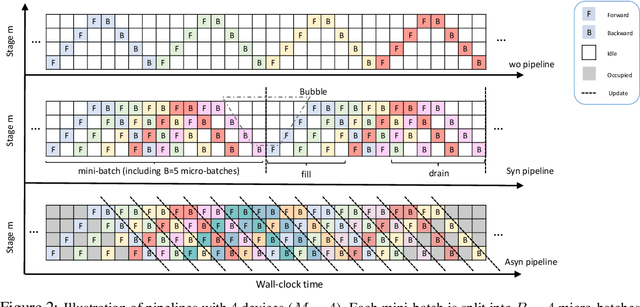
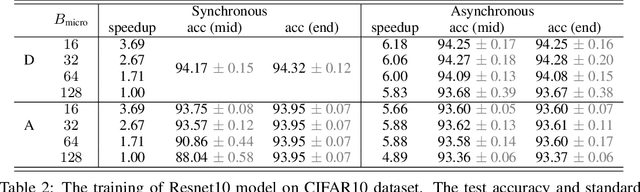
Aiming to accelerate the training of large deep neural models (DNN) in an energy-efficient way, an analog in-memory computing (AIMC) accelerator emerges as a solution with immense potential. In AIMC accelerators, trainable weights are kept in memory without the need to move from memory to processors during the training, reducing a bunch of overhead. However, although the in-memory feature enables efficient computation, it also constrains the use of data parallelism since copying weights from one AIMC to another is expensive. To enable parallel training using AIMC, we propose synchronous and asynchronous pipeline parallelism for AIMC accelerators inspired by the pipeline in digital domains. This paper provides a theoretical convergence guarantee for both synchronous and asynchronous pipelines in terms of both sampling and clock cycle complexity, which is non-trivial since the physical characteristic of AIMC accelerators leads to analog updates that suffer from asymmetric bias. The simulations of training DNN on real datasets verify the efficiency of pipeline training.

Single-Timescale Multi-Sequence Stochastic Approximation Without Fixed Point Smoothness: Theories and Applications

Stochastic approximation (SA) that involves multiple coupled sequences, known as multiple-sequence SA (MSSA), finds diverse applications in the fields of signal processing and machine learning. However, existing theoretical understandings {of} MSSA are limited: the multi-timescale analysis implies a slow convergence rate, whereas the single-timescale analysis relies on a stringent fixed point smoothness assumption. This paper establishes tighter single-timescale analysis for MSSA, without assuming smoothness of the fixed points. Our theoretical findings reveal that, when all involved operators are strongly monotone, MSSA converges at a rate of $\tilde{\mathcal{O}}(K^{-1})$, where $K$ denotes the total number of iterations. In addition, when all involved operators are strongly monotone except for the main one, MSSA converges at a rate of $\mathcal{O}(K^{-\frac{1}{2}})$. These theoretical findings align with those established for single-sequence SA. Applying these theoretical findings to bilevel optimization and communication-efficient distributed learning offers relaxed assumptions and/or simpler algorithms with performance guarantees, as validated by numerical experiments.

On the Trade-off between Flatness and Optimization in Distributed Learning

This paper proposes a theoretical framework to evaluate and compare the performance of gradient-descent algorithms for distributed learning in relation to their behavior around local minima in nonconvex environments. Previous works have noticed that convergence toward flat local minima tend to enhance the generalization ability of learning algorithms. This work discovers two interesting results. First, it shows that decentralized learning strategies are able to escape faster away from local minimizers and favor convergence toward flatter minima relative to the centralized solution in the large-batch training regime. Second, and importantly, the ultimate classification accuracy is not solely dependent on the flatness of the local minimizer but also on how well a learning algorithm can approach that minimum. In other words, the classification accuracy is a function of both flatness and optimization performance. The paper examines the interplay between the two measures of flatness and optimization error closely. One important conclusion is that decentralized strategies of the diffusion type deliver enhanced classification accuracy because it strikes a more favorable balance between flatness and optimization performance.

Towards Exact Gradient-based Training on Analog In-memory Computing

Given the high economic and environmental costs of using large vision or language models, analog in-memory accelerators present a promising solution for energy-efficient AI. While inference on analog accelerators has been studied recently, the training perspective is underexplored. Recent studies have shown that the "workhorse" of digital AI training - stochastic gradient descent (SGD) algorithm converges inexactly when applied to model training on non-ideal devices. This paper puts forth a theoretical foundation for gradient-based training on analog devices. We begin by characterizing the non-convergent issue of SGD, which is caused by the asymmetric updates on the analog devices. We then provide a lower bound of the asymptotic error to show that there is a fundamental performance limit of SGD-based analog training rather than an artifact of our analysis. To address this issue, we study a heuristic analog algorithm called Tiki-Taka that has recently exhibited superior empirical performance compared to SGD and rigorously show its ability to exactly converge to a critical point and hence eliminates the asymptotic error. The simulations verify the correctness of the analyses.

Byzantine-Robust Distributed Online Learning: Taming Adversarial Participants in An Adversarial Environment

This paper studies distributed online learning under Byzantine attacks. The performance of an online learning algorithm is often characterized by (adversarial) regret, which evaluates the quality of one-step-ahead decision-making when an environment provides adversarial losses, and a sublinear bound is preferred. But we prove that, even with a class of state-of-the-art robust aggregation rules, in an adversarial environment and in the presence of Byzantine participants, distributed online gradient descent can only achieve a linear adversarial regret bound, which is tight. This is the inevitable consequence of Byzantine attacks, even though we can control the constant of the linear adversarial regret to a reasonable level. Interestingly, when the environment is not fully adversarial so that the losses of the honest participants are i.i.d. (independent and identically distributed), we show that sublinear stochastic regret, in contrast to the aforementioned adversarial regret, is possible. We develop a Byzantine-robust distributed online momentum algorithm to attain such a sublinear stochastic regret bound. Extensive numerical experiments corroborate our theoretical analysis.

Byzantine-Robust Variance-Reduced Federated Learning over Distributed Non-i.i.d. Data

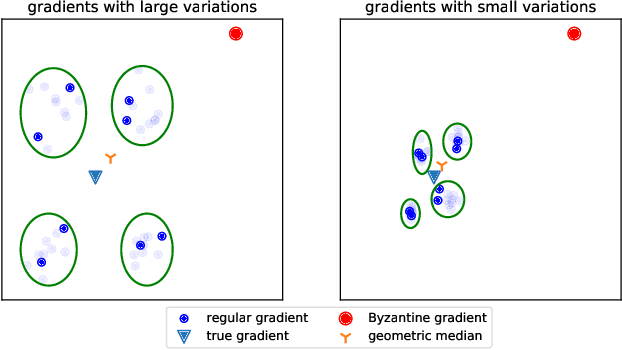
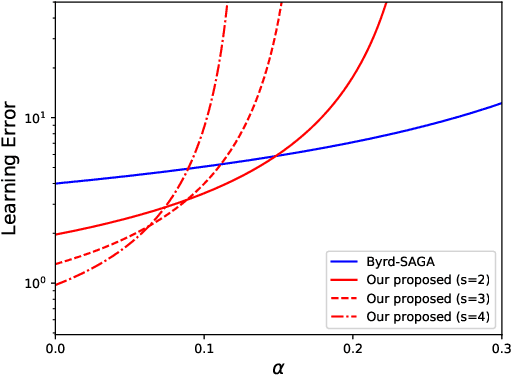
We propose a Byzantine-robust variance-reduced stochastic gradient descent (SGD) method to solve the distributed finite-sum minimization problem when the data on the workers are not independent and identically distributed (i.i.d.). During the learning process, an unknown number of Byzantine workers may send malicious messages to the master node, leading to remarkable learning error. Most of the Byzantine-robust methods address this issue by using robust aggregation rules to aggregate the received messages, but rely on the assumption that all the regular workers have i.i.d. data, which is not the case in many federated learning applications. In light of the significance of reducing stochastic gradient noise for mitigating the effect of Byzantine attacks, we use a resampling strategy to reduce the impact of both inner variation (that describes the sample heterogeneity on every regular worker) and outer variation (that describes the sample heterogeneity among the regular workers), along with a stochastic average gradient algorithm (SAGA) to fully eliminate the inner variation. The variance-reduced messages are then aggregated with a robust geometric median operator. Under certain conditions, we prove that the proposed method reaches a neighborhood of the optimal solution with linear convergence rate, and the learning error is much smaller than those given by the state-of-the-art methods in the non-i.i.d. setting. Numerical experiments corroborate the theoretical results and show satisfactory performance of the proposed method.

Federated Variance-Reduced Stochastic Gradient Descent with Robustness to Byzantine Attacks

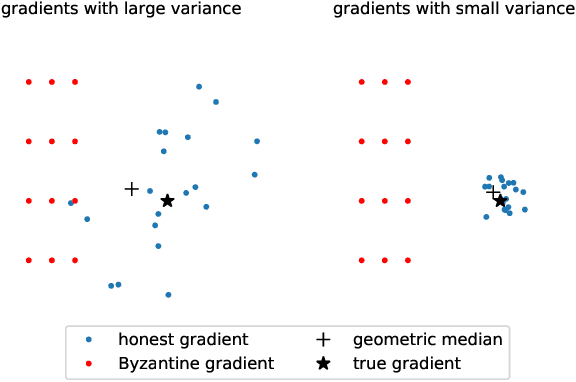
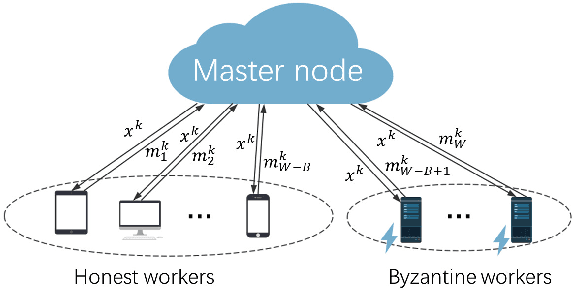
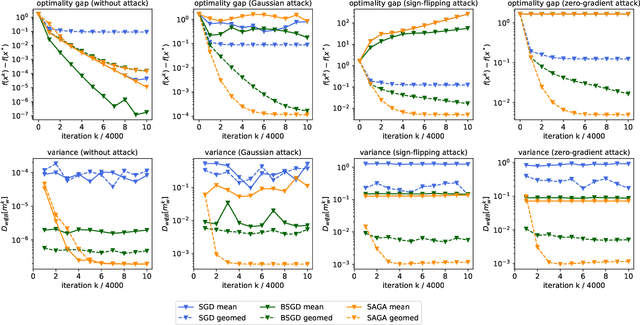
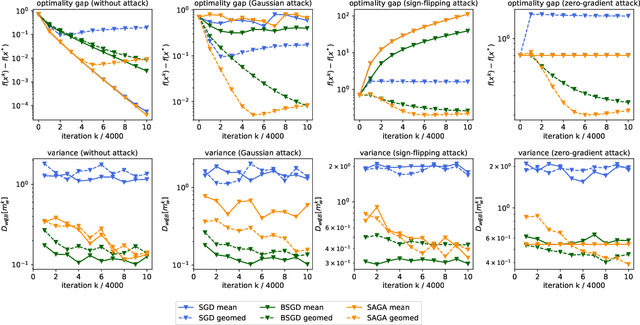
This paper deals with distributed finite-sum optimization for learning over networks in the presence of malicious Byzantine attacks. To cope with such attacks, most resilient approaches so far combine stochastic gradient descent (SGD) with different robust aggregation rules. However, the sizeable SGD-induced stochastic gradient noise makes it challenging to distinguish malicious messages sent by the Byzantine attackers from noisy stochastic gradients sent by the 'honest' workers. This motivates us to reduce the variance of stochastic gradients as a means of robustifying SGD in the presence of Byzantine attacks. To this end, the present work puts forth a Byzantine attack resilient distributed (Byrd-) SAGA approach for learning tasks involving finite-sum optimization over networks. Rather than the mean employed by distributed SAGA, the novel Byrd- SAGA relies on the geometric median to aggregate the corrected stochastic gradients sent by the workers. When less than half of the workers are Byzantine attackers, the robustness of geometric median to outliers enables Byrd-SAGA to attain provably linear convergence to a neighborhood of the optimal solution, with the asymptotic learning error determined by the number of Byzantine workers. Numerical tests corroborate the robustness to various Byzantine attacks, as well as the merits of Byrd- SAGA over Byzantine attack resilient distributed SGD.