Tayfun Gokmen
Assessing the Performance of Analog Training for Transfer Learning
May 16, 2025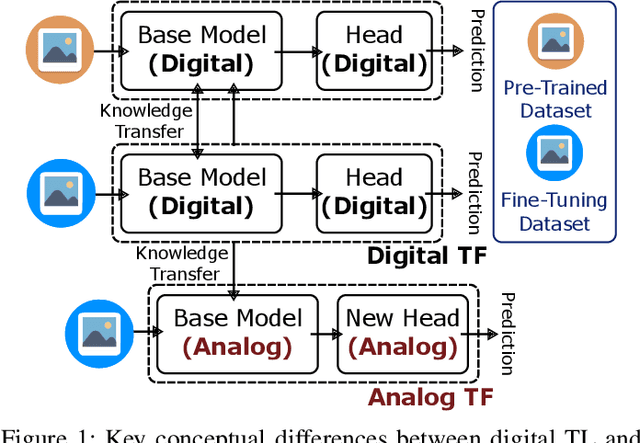
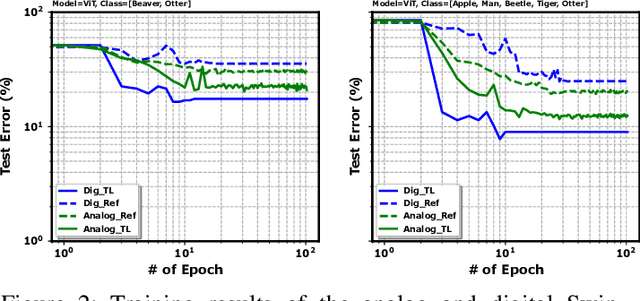
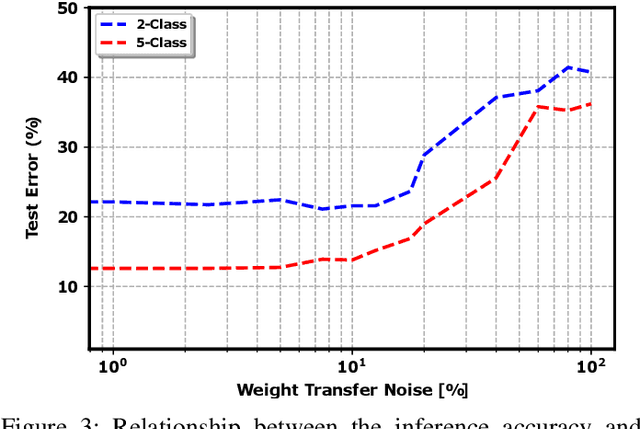
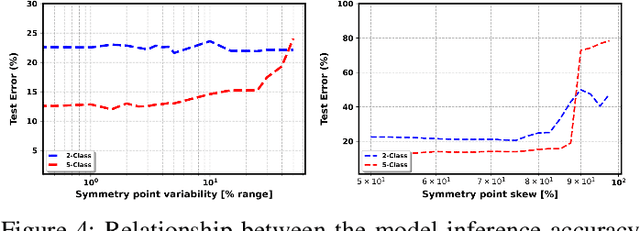
Abstract:Analog in-memory computing is a next-generation computing paradigm that promises fast, parallel, and energy-efficient deep learning training and transfer learning (TL). However, achieving this promise has remained elusive due to a lack of suitable training algorithms. Analog memory devices exhibit asymmetric and non-linear switching behavior in addition to device-to-device variation, meaning that most, if not all, of the current off-the-shelf training algorithms cannot achieve good training outcomes. Also, recently introduced algorithms have enjoyed limited attention, as they require bi-directionally switching devices of unrealistically high symmetry and precision and are highly sensitive. A new algorithm chopped TTv2 (c-TTv2), has been introduced, which leverages the chopped technique to address many of the challenges mentioned above. In this paper, we assess the performance of the c-TTv2 algorithm for analog TL using a Swin-ViT model on a subset of the CIFAR100 dataset. We also investigate the robustness of our algorithm to changes in some device specifications, including weight transfer noise, symmetry point skew, and symmetry point variability
Analog In-memory Training on General Non-ideal Resistive Elements: The Impact of Response Functions
Feb 10, 2025



Abstract:As the economic and environmental costs of training and deploying large vision or language models increase dramatically, analog in-memory computing (AIMC) emerges as a promising energy-efficient solution. However, the training perspective, especially its training dynamic, is underexplored. In AIMC hardware, the trainable weights are represented by the conductance of resistive elements and updated using consecutive electrical pulses. Among all the physical properties of resistive elements, the response to the pulses directly affects the training dynamics. This paper first provides a theoretical foundation for gradient-based training on AIMC hardware and studies the impact of response functions. We demonstrate that noisy update and asymmetric response functions negatively impact Analog SGD by imposing an implicit penalty term on the objective. To overcome the issue, Tiki-Taka, a residual learning algorithm, converges exactly to a critical point by optimizing a main array and a residual array bilevelly. The conclusion is supported by simulations validating our theoretical insights.
Pipeline Gradient-based Model Training on Analog In-memory Accelerators
Oct 19, 2024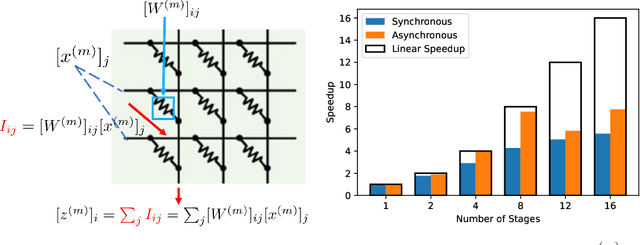

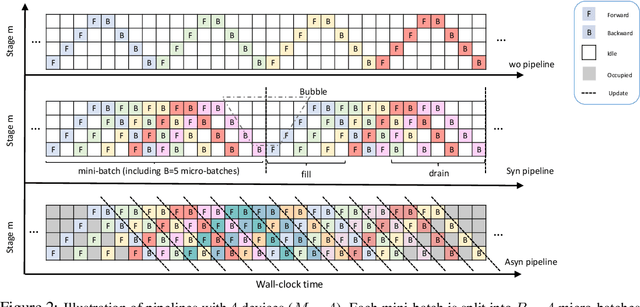
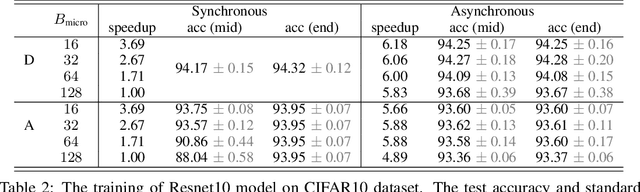
Abstract:Aiming to accelerate the training of large deep neural models (DNN) in an energy-efficient way, an analog in-memory computing (AIMC) accelerator emerges as a solution with immense potential. In AIMC accelerators, trainable weights are kept in memory without the need to move from memory to processors during the training, reducing a bunch of overhead. However, although the in-memory feature enables efficient computation, it also constrains the use of data parallelism since copying weights from one AIMC to another is expensive. To enable parallel training using AIMC, we propose synchronous and asynchronous pipeline parallelism for AIMC accelerators inspired by the pipeline in digital domains. This paper provides a theoretical convergence guarantee for both synchronous and asynchronous pipelines in terms of both sampling and clock cycle complexity, which is non-trivial since the physical characteristic of AIMC accelerators leads to analog updates that suffer from asymmetric bias. The simulations of training DNN on real datasets verify the efficiency of pipeline training.
Towards Exact Gradient-based Training on Analog In-memory Computing
Jun 18, 2024



Abstract:Given the high economic and environmental costs of using large vision or language models, analog in-memory accelerators present a promising solution for energy-efficient AI. While inference on analog accelerators has been studied recently, the training perspective is underexplored. Recent studies have shown that the "workhorse" of digital AI training - stochastic gradient descent (SGD) algorithm converges inexactly when applied to model training on non-ideal devices. This paper puts forth a theoretical foundation for gradient-based training on analog devices. We begin by characterizing the non-convergent issue of SGD, which is caused by the asymmetric updates on the analog devices. We then provide a lower bound of the asymptotic error to show that there is a fundamental performance limit of SGD-based analog training rather than an artifact of our analysis. To address this issue, we study a heuristic analog algorithm called Tiki-Taka that has recently exhibited superior empirical performance compared to SGD and rigorously show its ability to exactly converge to a critical point and hence eliminates the asymptotic error. The simulations verify the correctness of the analyses.
Fast offset corrected in-memory training
Mar 08, 2023Abstract:In-memory computing with resistive crossbar arrays has been suggested to accelerate deep-learning workloads in highly efficient manner. To unleash the full potential of in-memory computing, it is desirable to accelerate the training as well as inference for large deep neural networks (DNNs). In the past, specialized in-memory training algorithms have been proposed that not only accelerate the forward and backward passes, but also establish tricks to update the weight in-memory and in parallel. However, the state-of-the-art algorithm (Tiki-Taka version 2 (TTv2)) still requires near perfect offset correction and suffers from potential biases that might occur due to programming and estimation inaccuracies, as well as longer-term instabilities of the device materials. Here we propose and describe two new and improved algorithms for in-memory computing (Chopped-TTv2 (c-TTv2) and Analog Gradient Accumulation with Dynamic reference (AGAD)), that retain the same runtime complexity but correct for any remaining offsets using choppers. These algorithms greatly relax the device requirements and thus expanding the scope of possible materials potentially employed for such fast in-memory DNN training.
Neural Network Training with Asymmetric Crosspoint Elements
Jan 31, 2022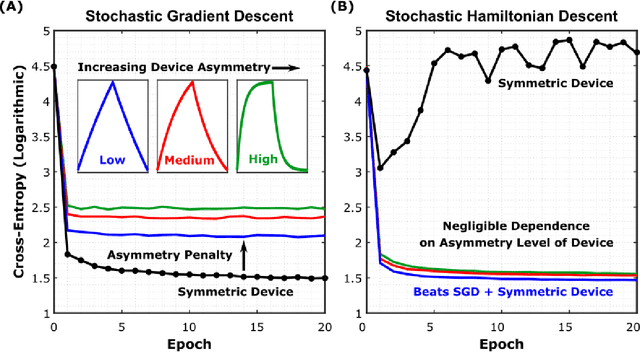
Abstract:Analog crossbar arrays comprising programmable nonvolatile resistors are under intense investigation for acceleration of deep neural network training. However, the ubiquitous asymmetric conductance modulation of practical resistive devices critically degrades the classification performance of networks trained with conventional algorithms. Here, we describe and experimentally demonstrate an alternative fully-parallel training algorithm: Stochastic Hamiltonian Descent. Instead of conventionally tuning weights in the direction of the error function gradient, this method programs the network parameters to successfully minimize the total energy (Hamiltonian) of the system that incorporates the effects of device asymmetry. We provide critical intuition on why device asymmetry is fundamentally incompatible with conventional training algorithms and how the new approach exploits it as a useful feature instead. Our technique enables immediate realization of analog deep learning accelerators based on readily available device technologies.
A flexible and fast PyTorch toolkit for simulating training and inference on analog crossbar arrays
Apr 05, 2021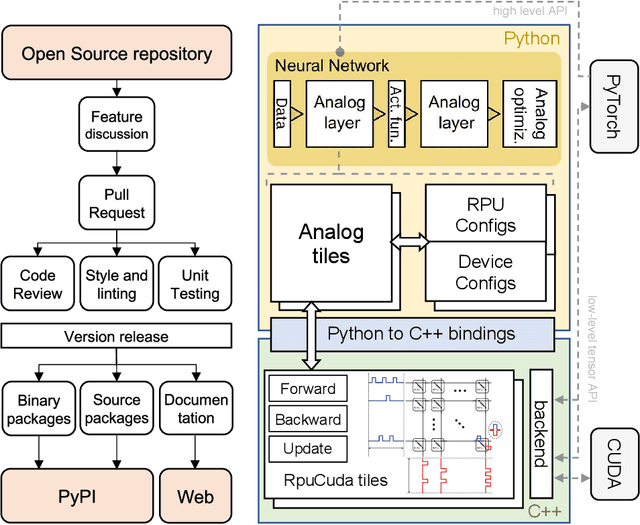


Abstract:We introduce the IBM Analog Hardware Acceleration Kit, a new and first of a kind open source toolkit to simulate analog crossbar arrays in a convenient fashion from within PyTorch (freely available at https://github.com/IBM/aihwkit). The toolkit is under active development and is centered around the concept of an "analog tile" which captures the computations performed on a crossbar array. Analog tiles are building blocks that can be used to extend existing network modules with analog components and compose arbitrary artificial neural networks (ANNs) using the flexibility of the PyTorch framework. Analog tiles can be conveniently configured to emulate a plethora of different analog hardware characteristics and their non-idealities, such as device-to-device and cycle-to-cycle variations, resistive device response curves, and weight and output noise. Additionally, the toolkit makes it possible to design custom unit cell configurations and to use advanced analog optimization algorithms such as Tiki-Taka. Moreover, the backward and update behavior can be set to "ideal" to enable hardware-aware training features for chips that target inference acceleration only. To evaluate the inference accuracy of such chips over time, we provide statistical programming noise and drift models calibrated on phase-change memory hardware. Our new toolkit is fully GPU accelerated and can be used to conveniently estimate the impact of material properties and non-idealities of future analog technology on the accuracy for arbitrary ANNs.
Algorithm for Training Neural Networks on Resistive Device Arrays
Sep 17, 2019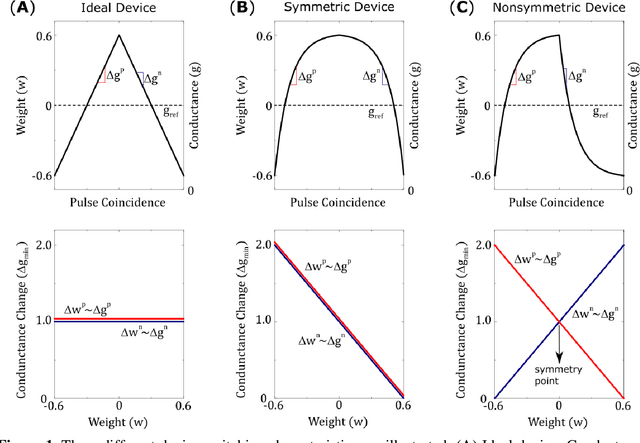
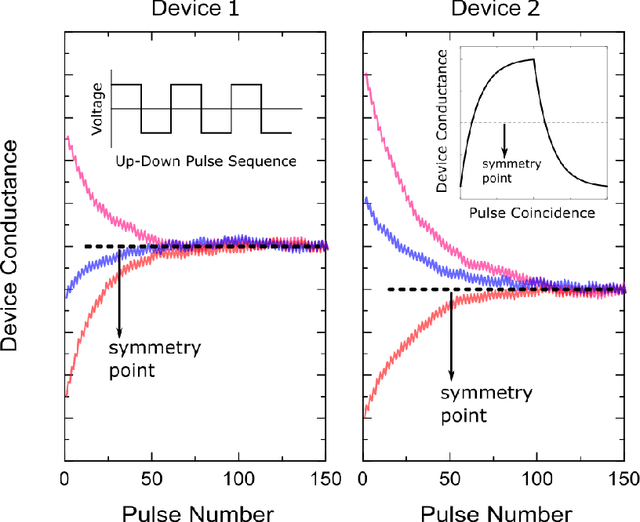

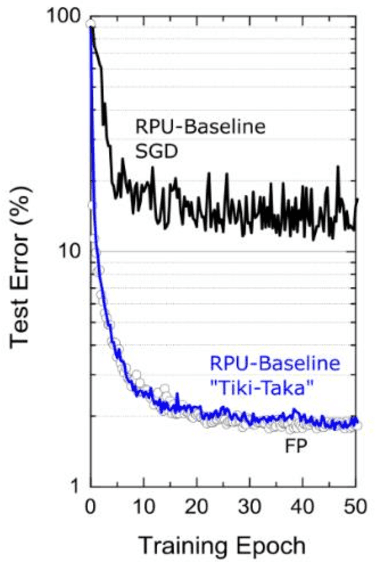
Abstract:Hardware architectures composed of resistive cross-point device arrays can provide significant power and speed benefits for deep neural network training workloads using stochastic gradient descent (SGD) and backpropagation (BP) algorithm. The training accuracy on this imminent analog hardware however strongly depends on the switching characteristics of the cross-point elements. One of the key requirements is that these resistive devices must change conductance in a symmetrical fashion when subjected to positive or negative pulse stimuli. Here, we present a new training algorithm, so-called the "Tiki-Taka" algorithm, that eliminates this stringent symmetry requirement. We show that device asymmetry introduces an unintentional implicit cost term into the SGD algorithm, whereas in the "Tiki-Taka" algorithm a coupled dynamical system simultaneously minimizes the original objective function of the neural network and the unintentional cost term due to device asymmetry in a self-consistent fashion. We tested the validity of this new algorithm on a range of network architectures such as fully connected, convolutional and LSTM networks. Simulation results on these various networks show that whatever accuracy is achieved using the conventional SGD algorithm with symmetric (ideal) device switching characteristics the same accuracy is also achieved using the "Tiki-Taka" algorithm with non-symmetric (non-ideal) device switching characteristics. Moreover, all the operations performed on the arrays are still parallel and therefore the implementation cost of this new algorithm on array architectures is minimal; and it maintains the aforementioned power and speed benefits. These algorithmic improvements are crucial to relax the material specification and to realize technologically viable resistive crossbar arrays that outperform digital accelerators for similar training tasks.
Zero-shifting Technique for Deep Neural Network Training on Resistive Cross-point Arrays
Aug 02, 2019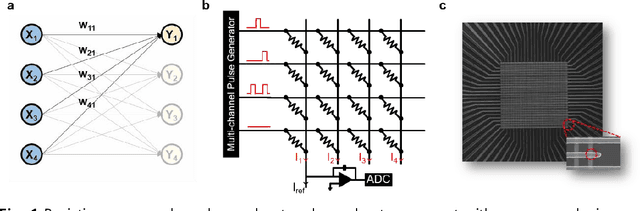
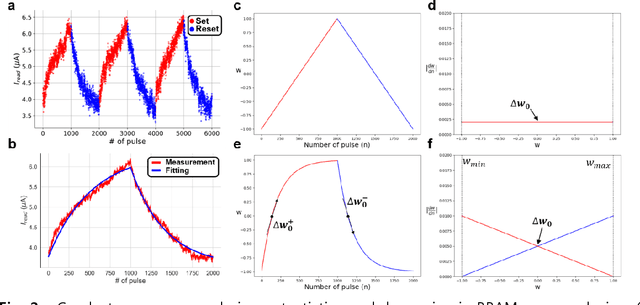
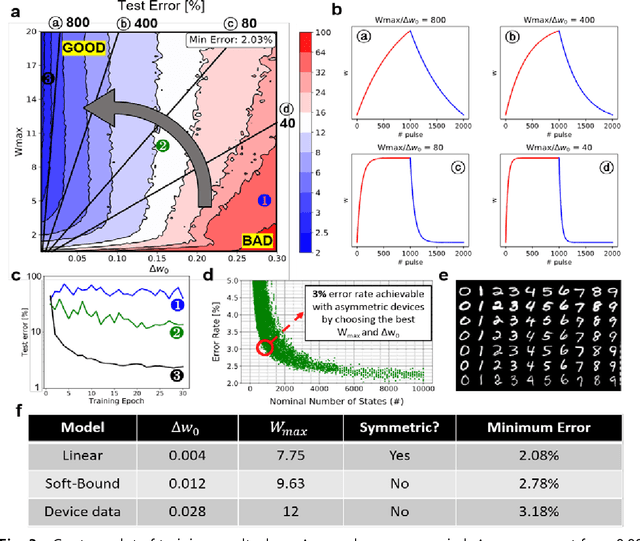
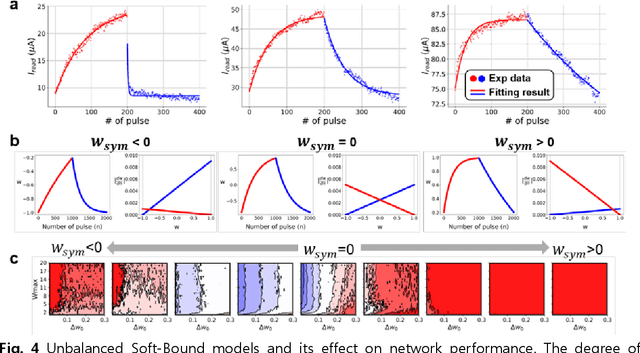
Abstract:A resistive memory device-based computing architecture is one of the promising platforms for energy-efficient Deep Neural Network (DNN) training accelerators. The key technical challenge in realizing such accelerators is to accumulate the gradient information without a bias. Unlike the digital numbers in software which can be assigned and accessed with desired accuracy, numbers stored in resistive memory devices can only be manipulated following the physics of the device, which can significantly limit the training performance. Therefore, additional techniques and algorithm-level remedies are required to achieve the best possible performance in resistive memory device-based accelerators. In this paper, we analyze asymmetric conductance modulation characteristics in RRAM by Soft-bound synapse model and present an in-depth analysis on the relationship between device characteristics and DNN model accuracy using a 3-layer DNN trained on the MNIST dataset. We show that the imbalance between up and down update leads to a poor network performance. We introduce a concept of symmetry point and propose a zero-shifting technique which can compensate imbalance by programming the reference device and changing the zero value point of the weight. By using this zero-shifting method, we show that network performance dramatically improves for imbalanced synapse devices.
Training large-scale ANNs on simulated resistive crossbar arrays
Jun 06, 2019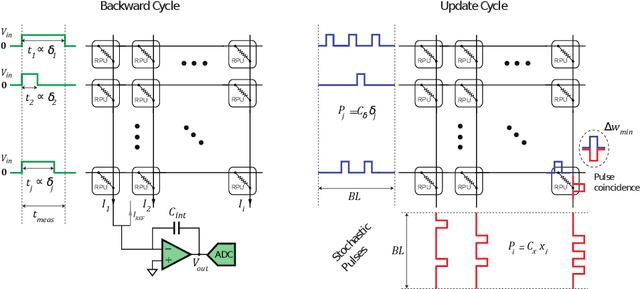
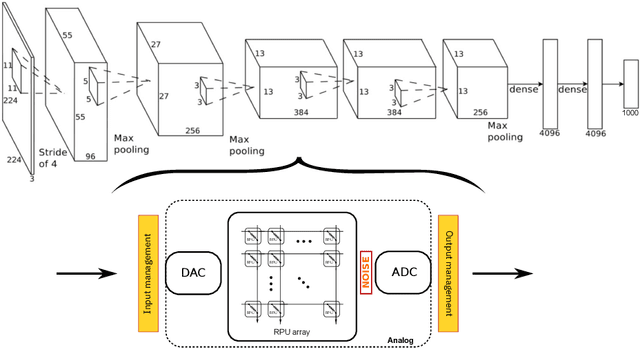
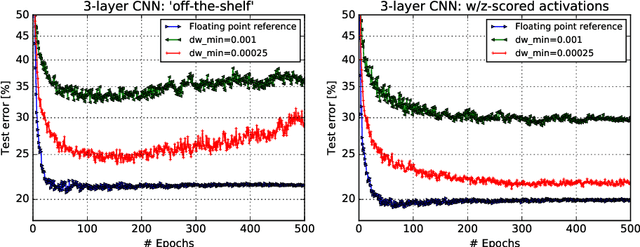
Abstract:Accelerating training of artificial neural networks (ANN) with analog resistive crossbar arrays is a promising idea. While the concept has been verified on very small ANNs and toy data sets (such as MNIST), more realistically sized ANNs and datasets have not yet been tackled. However, it is to be expected that device materials and hardware design constraints, such as noisy computations, finite number of resistive states of the device materials, saturating weight and activation ranges, and limited precision of analog-to-digital converters, will cause significant challenges to the successful training of state-of-the-art ANNs. By using analog hardware aware ANN training simulations, we here explore a number of simple algorithmic compensatory measures to cope with analog noise and limited weight and output ranges and resolutions, that dramatically improve the simulated training performances on RPU arrays on intermediately to large-scale ANNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge