AnalogNAS: A Neural Network Design Framework for Accurate Inference with Analog In-Memory Computing

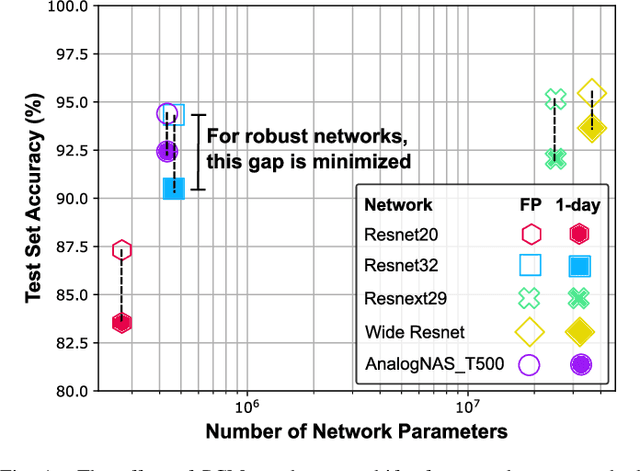
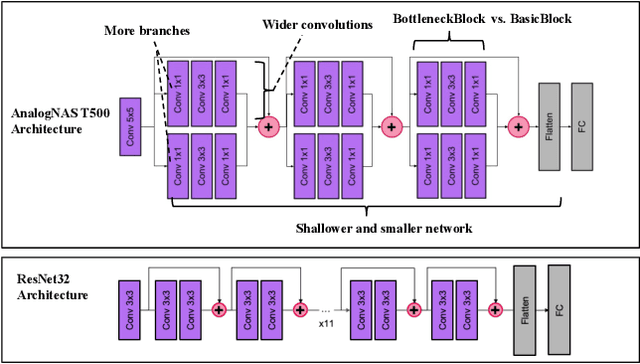
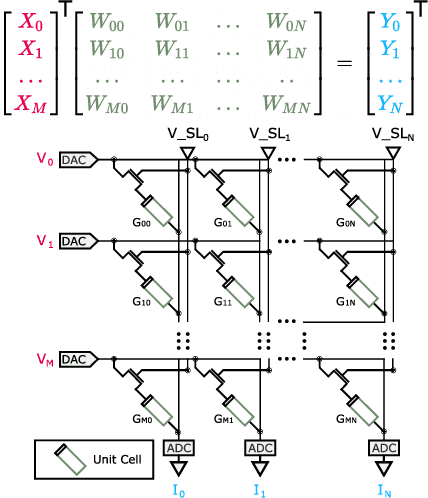
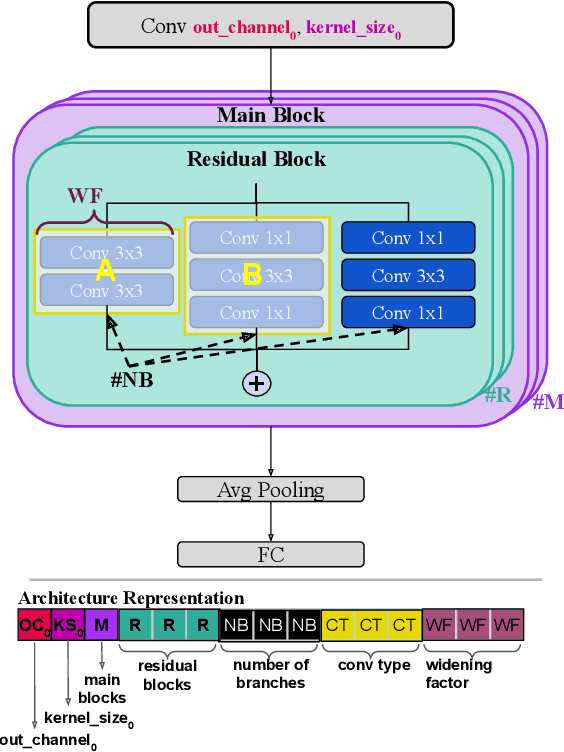
The advancement of Deep Learning (DL) is driven by efficient Deep Neural Network (DNN) design and new hardware accelerators. Current DNN design is primarily tailored for general-purpose use and deployment on commercially viable platforms. Inference at the edge requires low latency, compact and power-efficient models, and must be cost-effective. Digital processors based on typical von Neumann architectures are not conducive to edge AI given the large amounts of required data movement in and out of memory. Conversely, analog/mixed signal in-memory computing hardware accelerators can easily transcend the memory wall of von Neuman architectures when accelerating inference workloads. They offer increased area and power efficiency, which are paramount in edge resource-constrained environments. In this paper, we propose AnalogNAS, a framework for automated DNN design targeting deployment on analog In-Memory Computing (IMC) inference accelerators. We conduct extensive hardware simulations to demonstrate the performance of AnalogNAS on State-Of-The-Art (SOTA) models in terms of accuracy and deployment efficiency on various Tiny Machine Learning (TinyML) tasks. We also present experimental results that show AnalogNAS models achieving higher accuracy than SOTA models when implemented on a 64-core IMC chip based on Phase Change Memory (PCM). The AnalogNAS search code is released: https://github.com/IBM/analog-nas

Zero-shifting Technique for Deep Neural Network Training on Resistive Cross-point Arrays

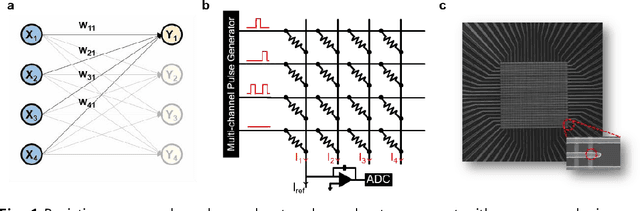
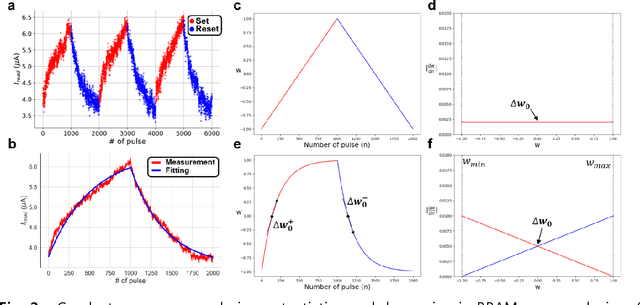
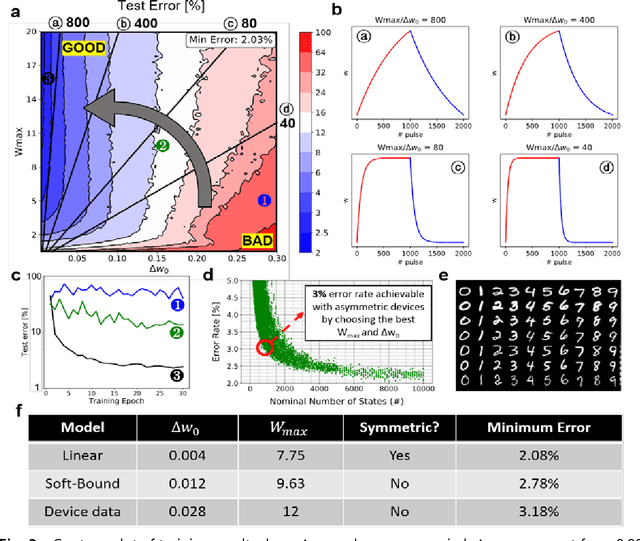
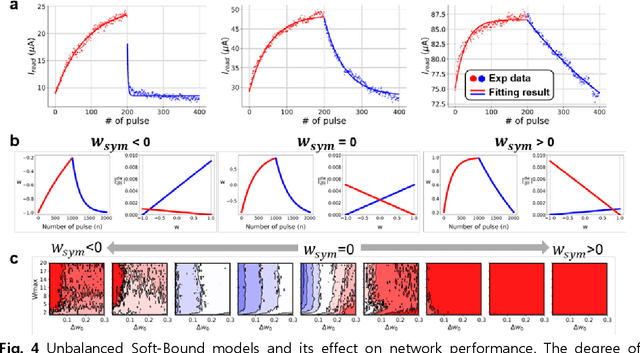
A resistive memory device-based computing architecture is one of the promising platforms for energy-efficient Deep Neural Network (DNN) training accelerators. The key technical challenge in realizing such accelerators is to accumulate the gradient information without a bias. Unlike the digital numbers in software which can be assigned and accessed with desired accuracy, numbers stored in resistive memory devices can only be manipulated following the physics of the device, which can significantly limit the training performance. Therefore, additional techniques and algorithm-level remedies are required to achieve the best possible performance in resistive memory device-based accelerators. In this paper, we analyze asymmetric conductance modulation characteristics in RRAM by Soft-bound synapse model and present an in-depth analysis on the relationship between device characteristics and DNN model accuracy using a 3-layer DNN trained on the MNIST dataset. We show that the imbalance between up and down update leads to a poor network performance. We introduce a concept of symmetry point and propose a zero-shifting technique which can compensate imbalance by programming the reference device and changing the zero value point of the weight. By using this zero-shifting method, we show that network performance dramatically improves for imbalanced synapse devices.

Training LSTM Networks with Resistive Cross-Point Devices

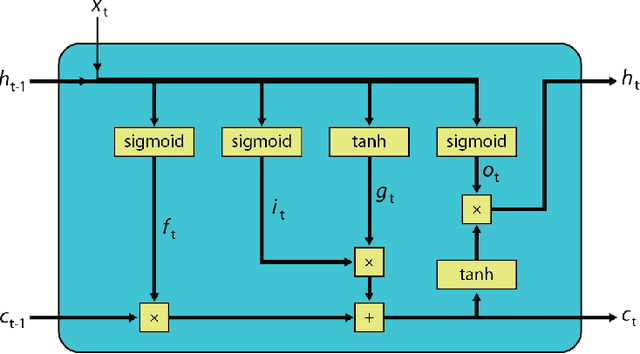
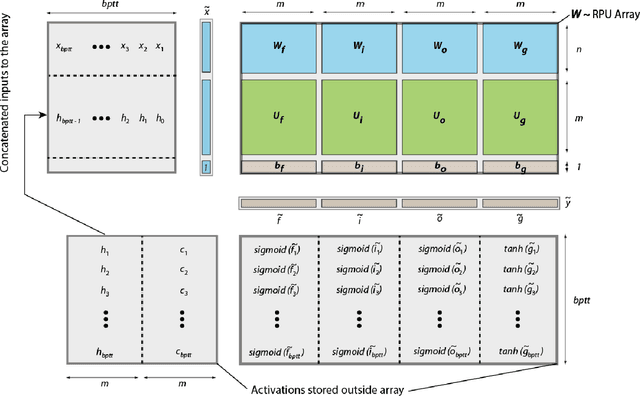
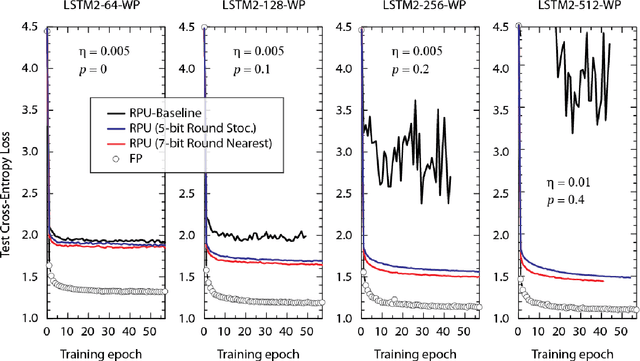
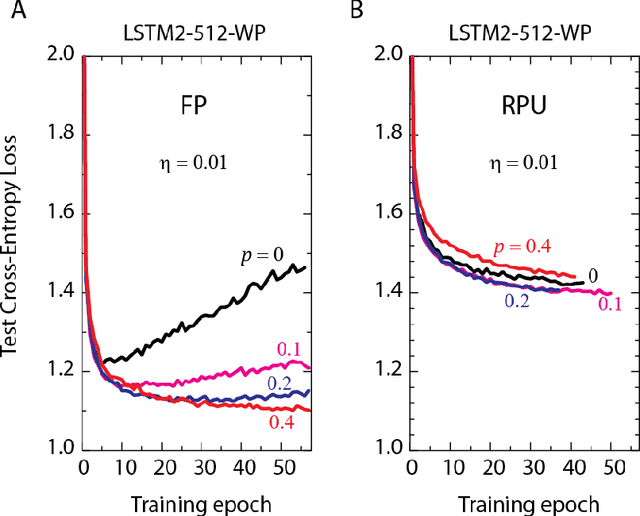
In our previous work we have shown that resistive cross point devices, so called Resistive Processing Unit (RPU) devices, can provide significant power and speed benefits when training deep fully connected networks as well as convolutional neural networks. In this work, we further extend the RPU concept for training recurrent neural networks (RNNs) namely LSTMs. We show that the mapping of recurrent layers is very similar to the mapping of fully connected layers and therefore the RPU concept can potentially provide large acceleration factors for RNNs as well. In addition, we study the effect of various device imperfections and system parameters on training performance. Symmetry of updates becomes even more crucial for RNNs; already a few percent asymmetry results in an increase in the test error compared to the ideal case trained with floating point numbers. Furthermore, the input signal resolution to device arrays needs to be at least 7 bits for successful training. However, we show that a stochastic rounding scheme can reduce the input signal resolution back to 5 bits. Further, we find that RPU device variations and hardware noise are enough to mitigate overfitting, so that there is less need for using dropout. We note that the models trained here are roughly 1500 times larger than the fully connected network trained on MNIST dataset in terms of the total number of multiplication and summation operations performed per epoch. Thus, here we attempt to study the validity of the RPU approach for large scale networks.