Neural Network Training with Asymmetric Crosspoint Elements

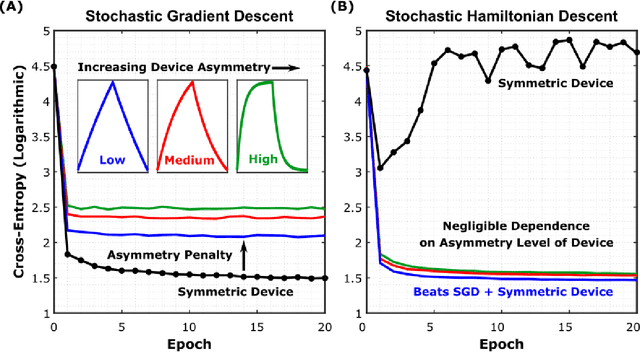
Analog crossbar arrays comprising programmable nonvolatile resistors are under intense investigation for acceleration of deep neural network training. However, the ubiquitous asymmetric conductance modulation of practical resistive devices critically degrades the classification performance of networks trained with conventional algorithms. Here, we describe and experimentally demonstrate an alternative fully-parallel training algorithm: Stochastic Hamiltonian Descent. Instead of conventionally tuning weights in the direction of the error function gradient, this method programs the network parameters to successfully minimize the total energy (Hamiltonian) of the system that incorporates the effects of device asymmetry. We provide critical intuition on why device asymmetry is fundamentally incompatible with conventional training algorithms and how the new approach exploits it as a useful feature instead. Our technique enables immediate realization of analog deep learning accelerators based on readily available device technologies.

Algorithm for Training Neural Networks on Resistive Device Arrays

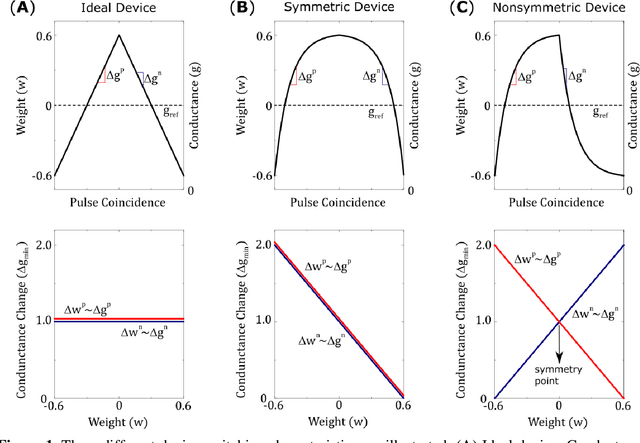
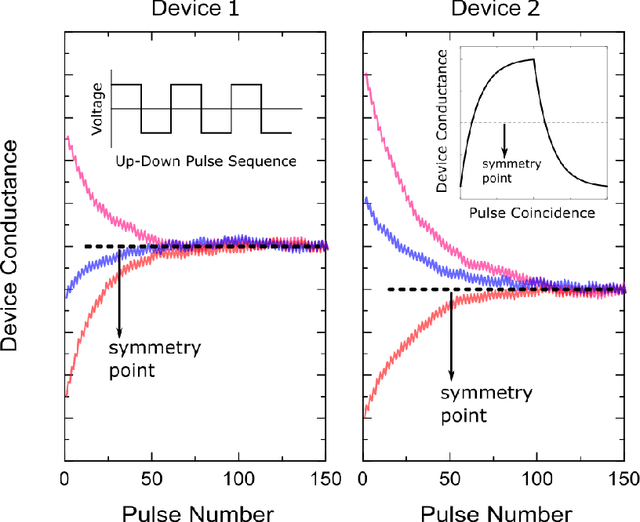
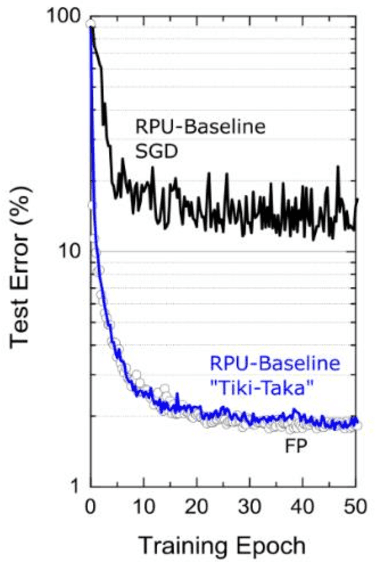
Hardware architectures composed of resistive cross-point device arrays can provide significant power and speed benefits for deep neural network training workloads using stochastic gradient descent (SGD) and backpropagation (BP) algorithm. The training accuracy on this imminent analog hardware however strongly depends on the switching characteristics of the cross-point elements. One of the key requirements is that these resistive devices must change conductance in a symmetrical fashion when subjected to positive or negative pulse stimuli. Here, we present a new training algorithm, so-called the "Tiki-Taka" algorithm, that eliminates this stringent symmetry requirement. We show that device asymmetry introduces an unintentional implicit cost term into the SGD algorithm, whereas in the "Tiki-Taka" algorithm a coupled dynamical system simultaneously minimizes the original objective function of the neural network and the unintentional cost term due to device asymmetry in a self-consistent fashion. We tested the validity of this new algorithm on a range of network architectures such as fully connected, convolutional and LSTM networks. Simulation results on these various networks show that whatever accuracy is achieved using the conventional SGD algorithm with symmetric (ideal) device switching characteristics the same accuracy is also achieved using the "Tiki-Taka" algorithm with non-symmetric (non-ideal) device switching characteristics. Moreover, all the operations performed on the arrays are still parallel and therefore the implementation cost of this new algorithm on array architectures is minimal; and it maintains the aforementioned power and speed benefits. These algorithmic improvements are crucial to relax the material specification and to realize technologically viable resistive crossbar arrays that outperform digital accelerators for similar training tasks.

Training large-scale ANNs on simulated resistive crossbar arrays

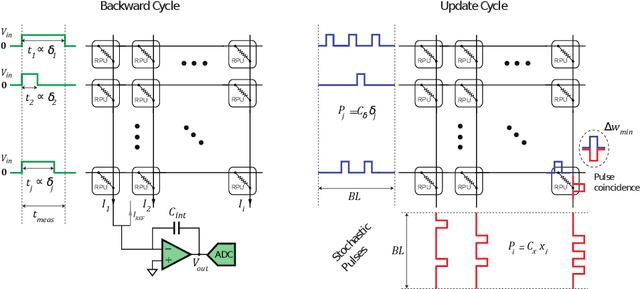
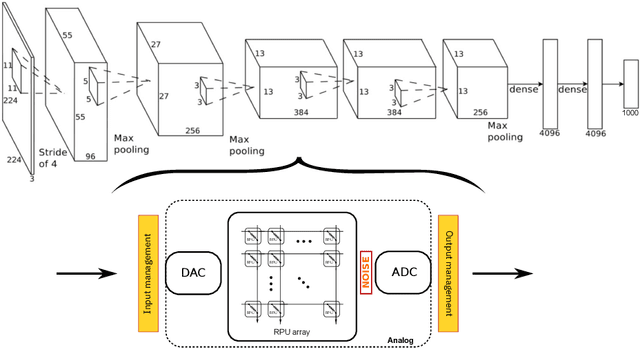
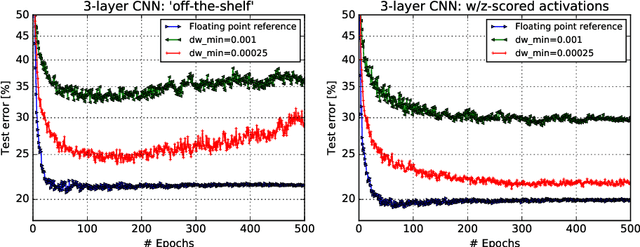
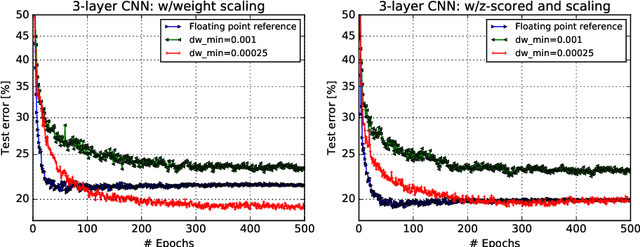
Accelerating training of artificial neural networks (ANN) with analog resistive crossbar arrays is a promising idea. While the concept has been verified on very small ANNs and toy data sets (such as MNIST), more realistically sized ANNs and datasets have not yet been tackled. However, it is to be expected that device materials and hardware design constraints, such as noisy computations, finite number of resistive states of the device materials, saturating weight and activation ranges, and limited precision of analog-to-digital converters, will cause significant challenges to the successful training of state-of-the-art ANNs. By using analog hardware aware ANN training simulations, we here explore a number of simple algorithmic compensatory measures to cope with analog noise and limited weight and output ranges and resolutions, that dramatically improve the simulated training performances on RPU arrays on intermediately to large-scale ANNs.

Efficient ConvNets for Analog Arrays

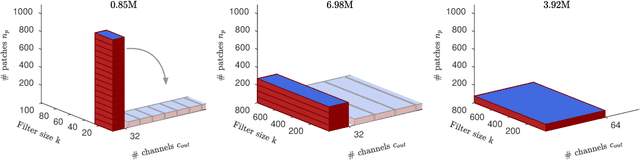
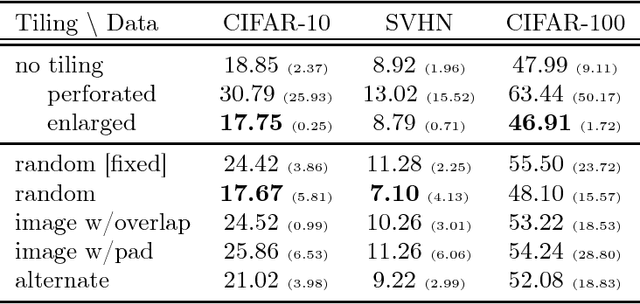
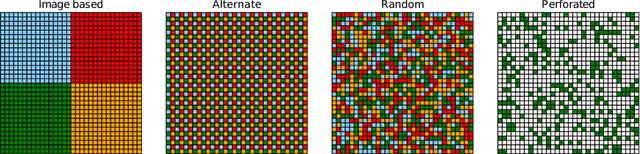
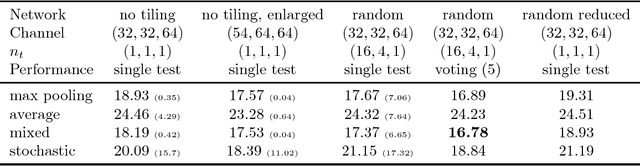
Analog arrays are a promising upcoming hardware technology with the potential to drastically speed up deep learning. Their main advantage is that they compute matrix-vector products in constant time, irrespective of the size of the matrix. However, early convolution layers in ConvNets map very unfavorably onto analog arrays, because kernel matrices are typically small and the constant time operation needs to be sequentially iterated a large number of times, reducing the speed up advantage for ConvNets. Here, we propose to replicate the kernel matrix of a convolution layer on distinct analog arrays, and randomly divide parts of the compute among them, so that multiple kernel matrices are trained in parallel. With this modification, analog arrays execute ConvNets with an acceleration factor that is proportional to the number of kernel matrices used per layer (here tested 16-128). Despite having more free parameters, we show analytically and in numerical experiments that this convolution architecture is self-regularizing and implicitly learns similar filters across arrays. We also report superior performance on a number of datasets and increased robustness to adversarial attacks. Our investigation suggests to revise the notion that mixed analog-digital hardware is not suitable for ConvNets.

Training LSTM Networks with Resistive Cross-Point Devices

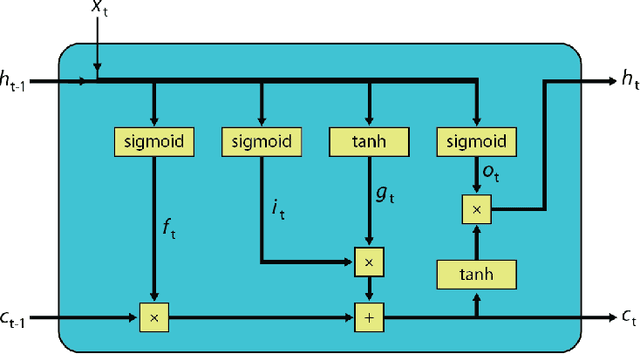
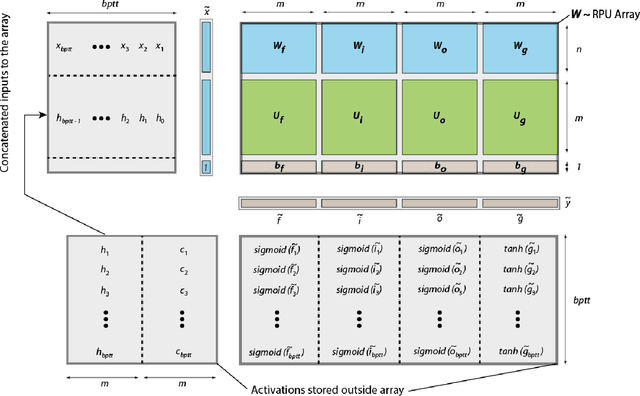
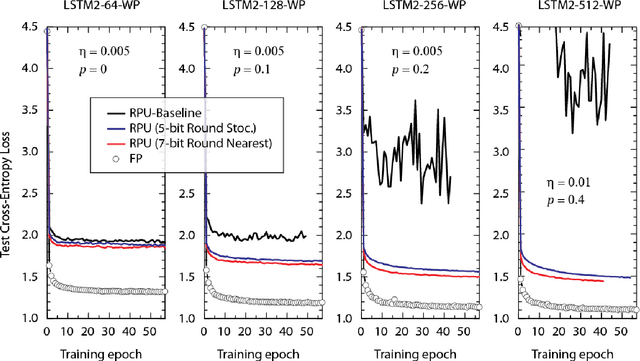
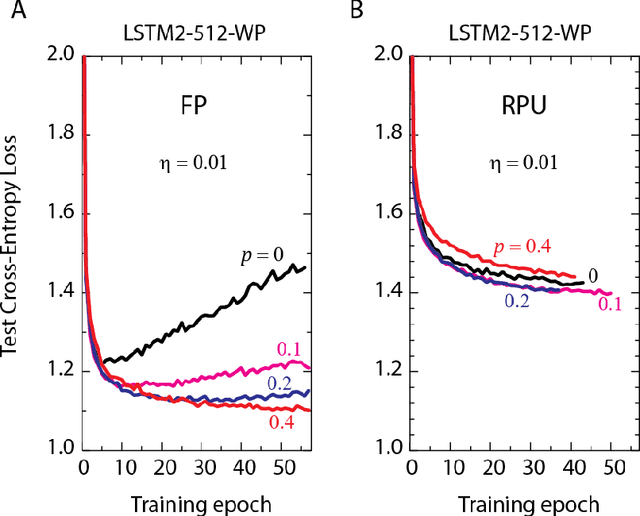
In our previous work we have shown that resistive cross point devices, so called Resistive Processing Unit (RPU) devices, can provide significant power and speed benefits when training deep fully connected networks as well as convolutional neural networks. In this work, we further extend the RPU concept for training recurrent neural networks (RNNs) namely LSTMs. We show that the mapping of recurrent layers is very similar to the mapping of fully connected layers and therefore the RPU concept can potentially provide large acceleration factors for RNNs as well. In addition, we study the effect of various device imperfections and system parameters on training performance. Symmetry of updates becomes even more crucial for RNNs; already a few percent asymmetry results in an increase in the test error compared to the ideal case trained with floating point numbers. Furthermore, the input signal resolution to device arrays needs to be at least 7 bits for successful training. However, we show that a stochastic rounding scheme can reduce the input signal resolution back to 5 bits. Further, we find that RPU device variations and hardware noise are enough to mitigate overfitting, so that there is less need for using dropout. We note that the models trained here are roughly 1500 times larger than the fully connected network trained on MNIST dataset in terms of the total number of multiplication and summation operations performed per epoch. Thus, here we attempt to study the validity of the RPU approach for large scale networks.

Training Deep Convolutional Neural Networks with Resistive Cross-Point Devices

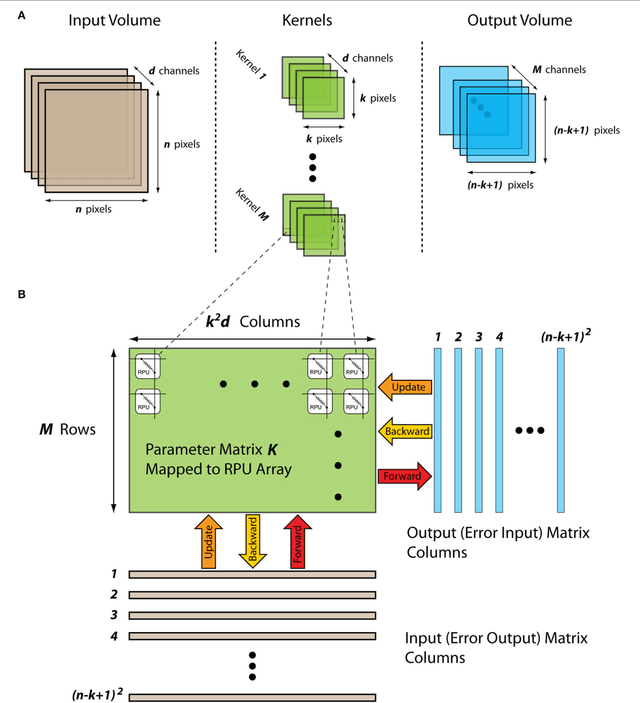
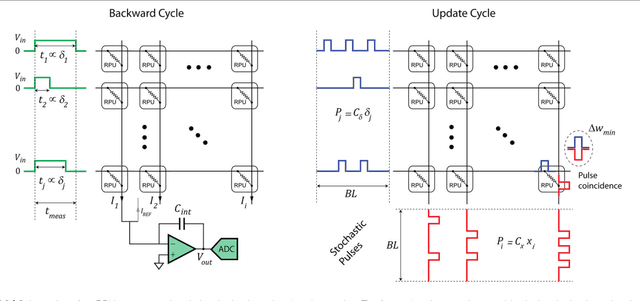
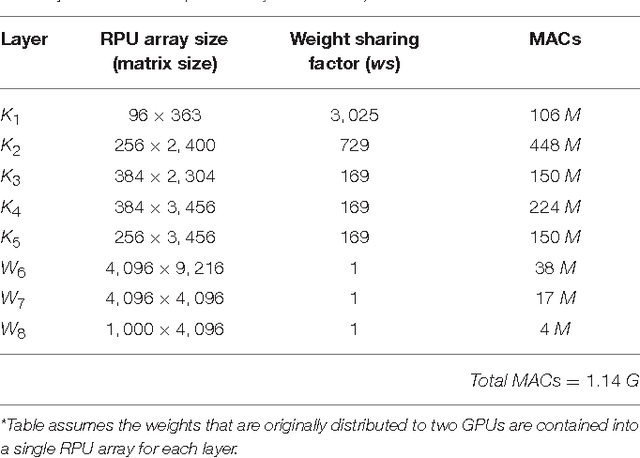
In a previous work we have detailed the requirements to obtain a maximal performance benefit by implementing fully connected deep neural networks (DNN) in form of arrays of resistive devices for deep learning. This concept of Resistive Processing Unit (RPU) devices we extend here towards convolutional neural networks (CNNs). We show how to map the convolutional layers to RPU arrays such that the parallelism of the hardware can be fully utilized in all three cycles of the backpropagation algorithm. We find that the noise and bound limitations imposed due to analog nature of the computations performed on the arrays effect the training accuracy of the CNNs. Noise and bound management techniques are presented that mitigate these problems without introducing any additional complexity in the analog circuits and can be addressed by the digital circuits. In addition, we discuss digitally programmable update management and device variability reduction techniques that can be used selectively for some of the layers in a CNN. We show that combination of all those techniques enables a successful application of the RPU concept for training CNNs. The techniques discussed here are more general and can be applied beyond CNN architectures and therefore enables applicability of RPU approach for large class of neural network architectures.