Byzantine-Robust Variance-Reduced Federated Learning over Distributed Non-i.i.d. Data

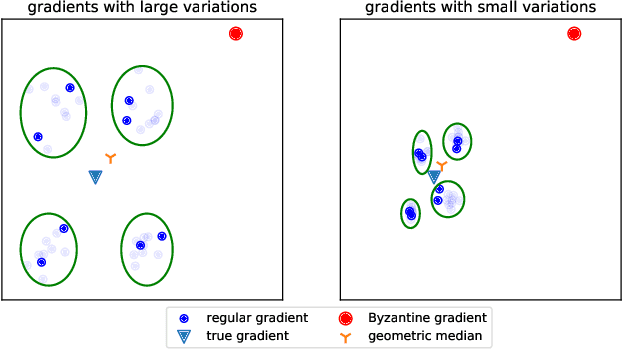
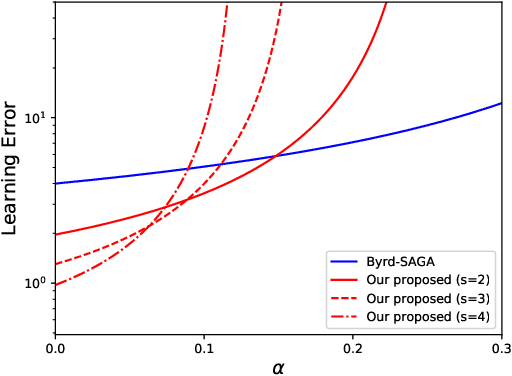
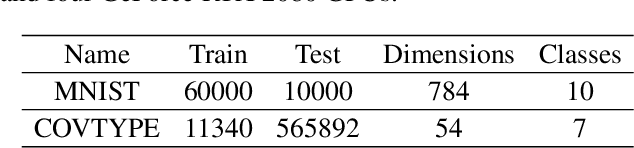
We propose a Byzantine-robust variance-reduced stochastic gradient descent (SGD) method to solve the distributed finite-sum minimization problem when the data on the workers are not independent and identically distributed (i.i.d.). During the learning process, an unknown number of Byzantine workers may send malicious messages to the master node, leading to remarkable learning error. Most of the Byzantine-robust methods address this issue by using robust aggregation rules to aggregate the received messages, but rely on the assumption that all the regular workers have i.i.d. data, which is not the case in many federated learning applications. In light of the significance of reducing stochastic gradient noise for mitigating the effect of Byzantine attacks, we use a resampling strategy to reduce the impact of both inner variation (that describes the sample heterogeneity on every regular worker) and outer variation (that describes the sample heterogeneity among the regular workers), along with a stochastic average gradient algorithm (SAGA) to fully eliminate the inner variation. The variance-reduced messages are then aggregated with a robust geometric median operator. Under certain conditions, we prove that the proposed method reaches a neighborhood of the optimal solution with linear convergence rate, and the learning error is much smaller than those given by the state-of-the-art methods in the non-i.i.d. setting. Numerical experiments corroborate the theoretical results and show satisfactory performance of the proposed method.