Fast Learning of Multidimensional Hawkes Processes via Frank-Wolfe

Hawkes processes have recently risen to the forefront of tools when it comes to modeling and generating sequential events data. Multidimensional Hawkes processes model both the self and cross-excitation between different types of events and have been applied successfully in various domain such as finance, epidemiology and personalized recommendations, among others. In this work we present an adaptation of the Frank-Wolfe algorithm for learning multidimensional Hawkes processes. Experimental results show that our approach has better or on par accuracy in terms of parameter estimation than other first order methods, while enjoying a significantly faster runtime.

Stochastic L-BFGS: Improved Convergence Rates and Practical Acceleration Strategies

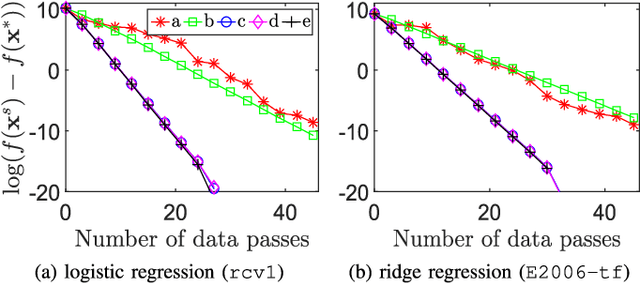
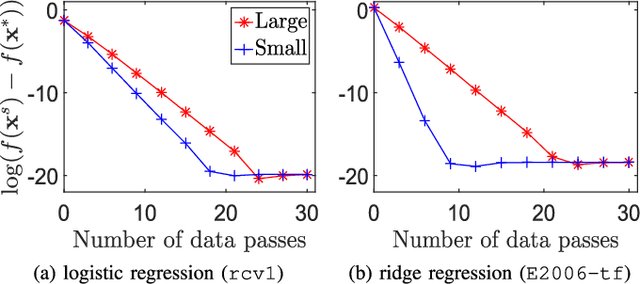
We revisit the stochastic limited-memory BFGS (L-BFGS) algorithm. By proposing a new framework for the convergence analysis, we prove improved convergence rates and computational complexities of the stochastic L-BFGS algorithms compared to previous works. In addition, we propose several practical acceleration strategies to speed up the empirical performance of such algorithms. We also provide theoretical analyses for most of the strategies. Experiments on large-scale logistic and ridge regression problems demonstrate that our proposed strategies yield significant improvements vis-\`a-vis competing state-of-the-art algorithms.

A Unified Convergence Analysis of the Multiplicative Update Algorithm for Regularized Nonnegative Matrix Factorization

The multiplicative update (MU) algorithm has been extensively used to estimate the basis and coefficient matrices in nonnegative matrix factorization (NMF) problems under a wide range of divergences and regularizers. However, theoretical convergence guarantees have only been derived for a few special divergences without regularization. In this work, we provide a conceptually simple, self-contained, and unified proof for the convergence of the MU algorithm applied on NMF with a wide range of divergences and regularizers. Our main result shows the sequence of iterates (i.e., pairs of basis and coefficient matrices) produced by the MU algorithm converges to the set of stationary points of the non-convex NMF optimization problem. Our proof strategy has the potential to open up new avenues for analyzing similar problems in machine learning and signal processing.

A Unified Framework for Stochastic Matrix Factorization via Variance Reduction

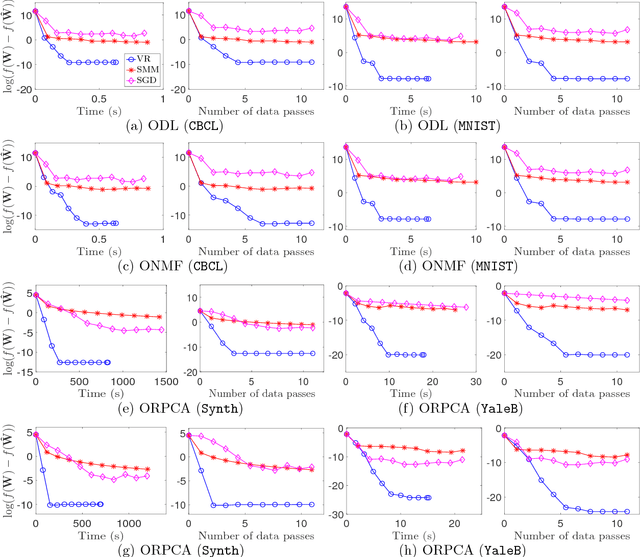
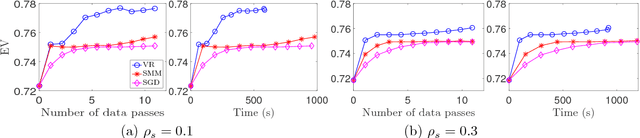
We propose a unified framework to speed up the existing stochastic matrix factorization (SMF) algorithms via variance reduction. Our framework is general and it subsumes several well-known SMF formulations in the literature. We perform a non-asymptotic convergence analysis of our framework and derive computational and sample complexities for our algorithm to converge to an $\epsilon$-stationary point in expectation. In addition, extensive experiments for a wide class of SMF formulations demonstrate that our framework consistently yields faster convergence and a more accurate output dictionary vis-\`a-vis state-of-the-art frameworks.

Online Nonnegative Matrix Factorization with Outliers

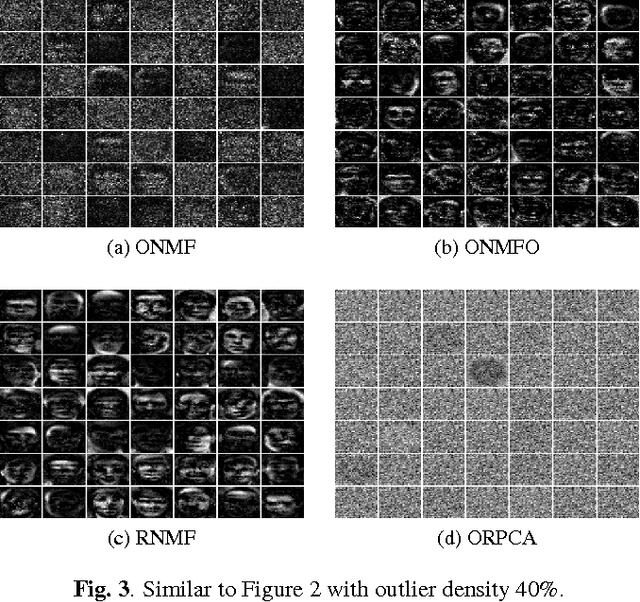
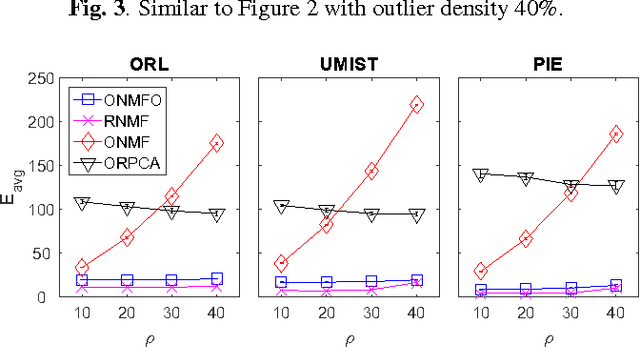
We propose a unified and systematic framework for performing online nonnegative matrix factorization in the presence of outliers. Our framework is particularly suited to large-scale data. We propose two solvers based on projected gradient descent and the alternating direction method of multipliers. We prove that the sequence of objective values converges almost surely by appealing to the quasi-martingale convergence theorem. We also show the sequence of learned dictionaries converges to the set of stationary points of the expected loss function almost surely. In addition, we extend our basic problem formulation to various settings with different constraints and regularizers. We also adapt the solvers and analyses to each setting. We perform extensive experiments on both synthetic and real datasets. These experiments demonstrate the computational efficiency and efficacy of our algorithms on tasks such as (parts-based) basis learning, image denoising, shadow removal and foreground-background separation.

Online Nonnegative Matrix Factorization with General Divergences

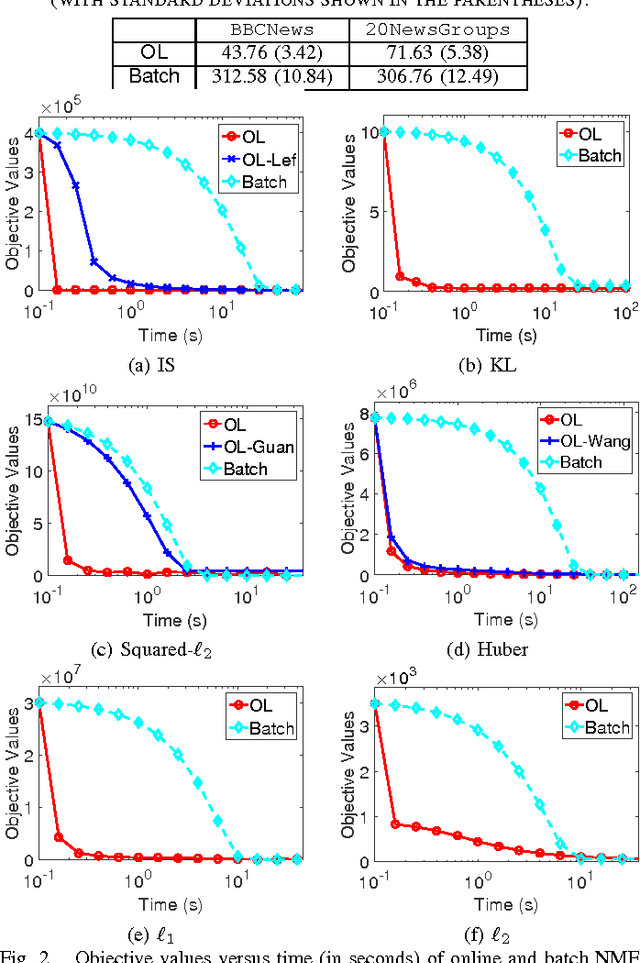
We develop a unified and systematic framework for performing online nonnegative matrix factorization under a wide variety of important divergences. The online nature of our algorithm makes it particularly amenable to large-scale data. We prove that the sequence of learned dictionaries converges almost surely to the set of critical points of the expected loss function. We do so by leveraging the theory of stochastic approximations and projected dynamical systems. This result substantially generalizes the previous results obtained only for the squared-$\ell_2$ loss. Moreover, the novel techniques involved in our analysis open new avenues for analyzing similar matrix factorization problems. The computational efficiency and the quality of the learned dictionary of our algorithm are verified empirically on both synthetic and real datasets. In particular, on the tasks of topic learning, shadow removal and image denoising, our algorithm achieves superior trade-offs between the quality of learned dictionary and running time over the batch and other online NMF algorithms.

Adversarial Top-$K$ Ranking

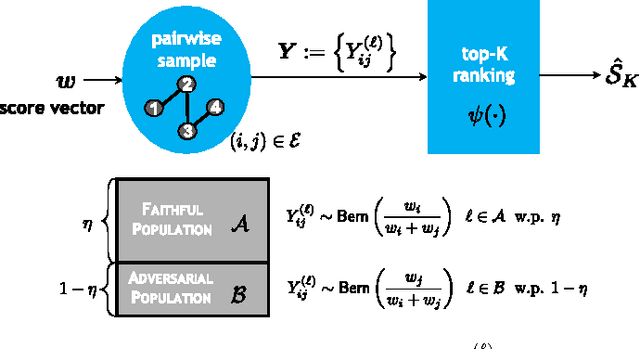
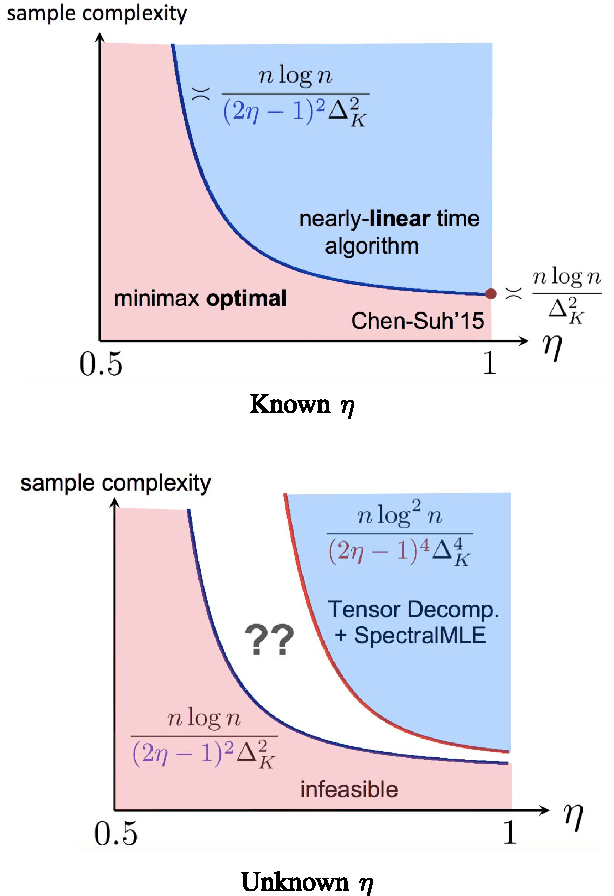
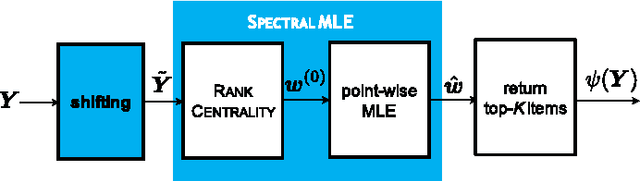
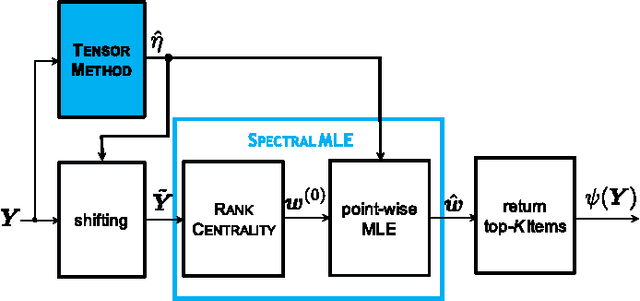
We study the top-$K$ ranking problem where the goal is to recover the set of top-$K$ ranked items out of a large collection of items based on partially revealed preferences. We consider an adversarial crowdsourced setting where there are two population sets, and pairwise comparison samples drawn from one of the populations follow the standard Bradley-Terry-Luce model (i.e., the chance of item $i$ beating item $j$ is proportional to the relative score of item $i$ to item $j$), while in the other population, the corresponding chance is inversely proportional to the relative score. When the relative size of the two populations is known, we characterize the minimax limit on the sample size required (up to a constant) for reliably identifying the top-$K$ items, and demonstrate how it scales with the relative size. Moreover, by leveraging a tensor decomposition method for disambiguating mixture distributions, we extend our result to the more realistic scenario in which the relative population size is unknown, thus establishing an upper bound on the fundamental limit of the sample size for recovering the top-$K$ set.