Learning to Price Supply Chain Contracts against a Learning Retailer

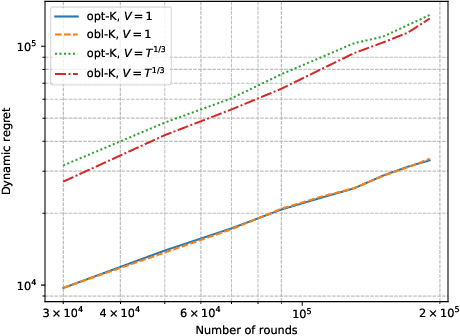
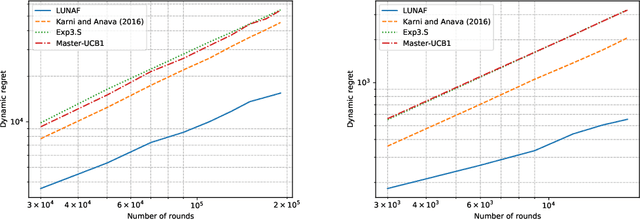
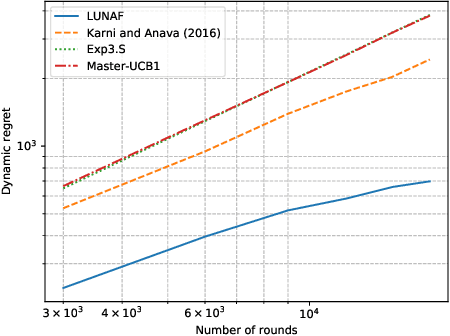
The rise of big data analytics has automated the decision-making of companies and increased supply chain agility. In this paper, we study the supply chain contract design problem faced by a data-driven supplier who needs to respond to the inventory decisions of the downstream retailer. Both the supplier and the retailer are uncertain about the market demand and need to learn about it sequentially. The goal for the supplier is to develop data-driven pricing policies with sublinear regret bounds under a wide range of possible retailer inventory policies for a fixed time horizon. To capture the dynamics induced by the retailer's learning policy, we first make a connection to non-stationary online learning by following the notion of variation budget. The variation budget quantifies the impact of the retailer's learning strategy on the supplier's decision-making. We then propose dynamic pricing policies for the supplier for both discrete and continuous demand. We also note that our proposed pricing policy only requires access to the support of the demand distribution, but critically, does not require the supplier to have any prior knowledge about the retailer's learning policy or the demand realizations. We examine several well-known data-driven policies for the retailer, including sample average approximation, distributionally robust optimization, and parametric approaches, and show that our pricing policies lead to sublinear regret bounds in all these cases. At the managerial level, we answer affirmatively that there is a pricing policy with a sublinear regret bound under a wide range of retailer's learning policies, even though she faces a learning retailer and an unknown demand distribution. Our work also provides a novel perspective in data-driven operations management where the principal has to learn to react to the learning policies employed by other agents in the system.

Convergence of Recursive Stochastic Algorithms using Wasserstein Divergence

This paper develops a unified framework, based on iterated random operator theory, to analyze the convergence of constant stepsize recursive stochastic algorithms (RSAs) in machine learning and reinforcement learning. RSAs use randomization to efficiently compute expectations, and so their iterates form a stochastic process. The key idea is to lift the RSA into an appropriate higher-dimensional space and then express it as an equivalent Markov chain. Instead of determining the convergence of this Markov chain (which may not converge under constant stepsize), we study the convergence of the distribution of this Markov chain. To study this, we define a new notion of Wasserstein divergence. We show that if the distribution of the iterates in the Markov chain satisfy certain contraction property with respect to the Wasserstein divergence, then the Markov chain admits an invariant distribution. Inspired by the SVRG algorithm, we develop a method to convert any RSA to a variance reduced RSA that converges to the optimal solution with in almost sure sense or in probability. We show that convergence of a large family of constant stepsize RSAs can be understood using this framework. We apply this framework to ascertain the convergence of mini-batch SGD, forward-backward splitting with catalyst, SVRG, SAGA, empirical Q value iteration, synchronous Q-learning, enhanced policy iteration, and MDPs with a generative model. We also develop two new algorithms for reinforcement learning and establish their convergence using this framework.

A Unifying Framework for Variance Reduction Algorithms for Finding Zeroes of Monotone Operators

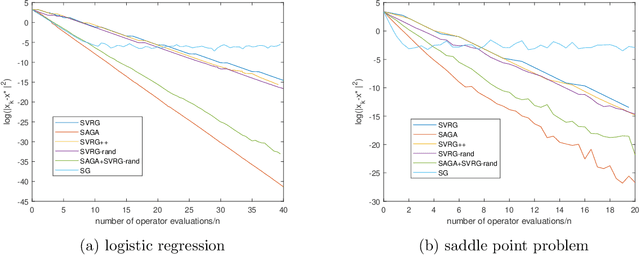
A wide range of optimization problems can be recast as monotone inclusion problems. We propose a unifying framework for solving the monotone inclusion problem with randomized Forward-Backward algorithms. Our framework covers many existing deterministic and stochastic algorithms. Under various conditions, we can establish both sublinear and linear convergence rates in expectation for the algorithms covered by this framework. In addition, we consider algorithm design as well as asynchronous randomized Forward algorithms. Numerical experiments demonstrate the worth of the new algorithms that emerge from our framework

Preference Elicitation and Robust Optimization with Multi-Attribute Quasi-Concave Choice Functions

Decision maker's preferences are often captured by some choice functions which are used to rank prospects. In this paper, we consider ambiguity in choice functions over a multi-attribute prospect space. Our main result is a robust preference model where the optimal decision is based on the worst-case choice function from an ambiguity set constructed through preference elicitation with pairwise comparisons of prospects. Differing from existing works in the area, our focus is on quasi-concave choice functions rather than concave functions and this enables us to cover a wide range of utility/risk preference problems including multi-attribute expected utility and $S$-shaped aspirational risk preferences. The robust choice function is increasing and quasi-concave but not necessarily translation invariant, a key property of monetary risk measures. We propose two approaches based respectively on the support functions and level functions of quasi-concave functions to develop tractable formulations of the maximin preference robust optimization model. The former gives rise to a mixed integer linear programming problem whereas the latter is equivalent to solving a sequence of convex risk minimization problems. To assess the effectiveness of the proposed robust preference optimization model and numerical schemes, we apply them to a security budget allocation problem and report some preliminary results from experiments.

Stochastic Approximation for Risk-aware Markov Decision Processes

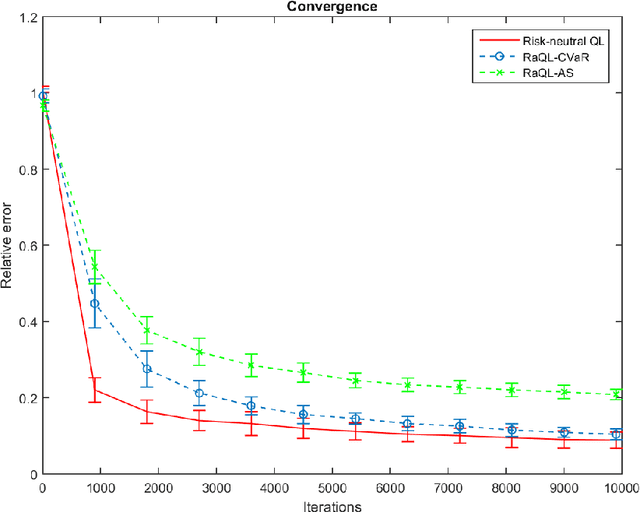
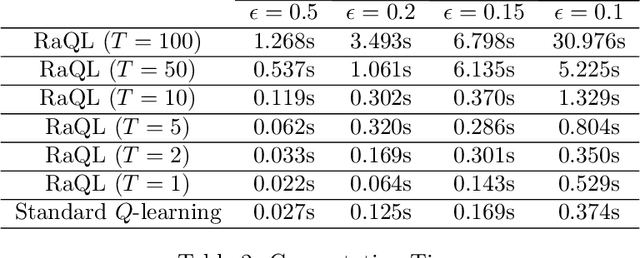
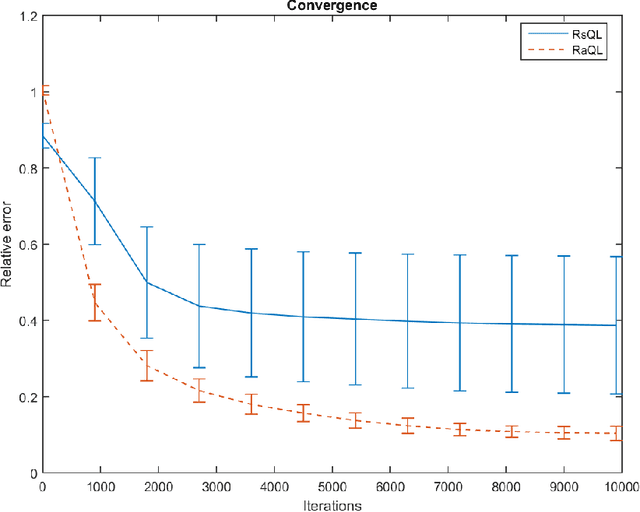
In this paper, we develop a stochastic approximation type algorithm to solve finite state and action, infinite-horizon, risk-aware Markov decision processes. Our algorithm is based on solving stochastic saddle-point problems for risk estimation and doing $Q$-learning for finding the optimal risk-aware policy. We show that several widely investigated risk measures (e.g. conditional value-at-risk, optimized certainty equivalent, and absolute semi-deviation) can be expressed as such stochastic saddle-point problems. We establish the almost sure convergence and convergence rate results for our overall algorithm. For error tolerance $\epsilon$ and learning rate $k$, the convergence rate of our algorithm is $\Omega((\ln(1/\delta\epsilon)/\epsilon^{2})^{1/k}+(\ln(1/\epsilon))^{1/(1-k)})$ with probability $1-\delta$.

Stochastic L-BFGS: Improved Convergence Rates and Practical Acceleration Strategies

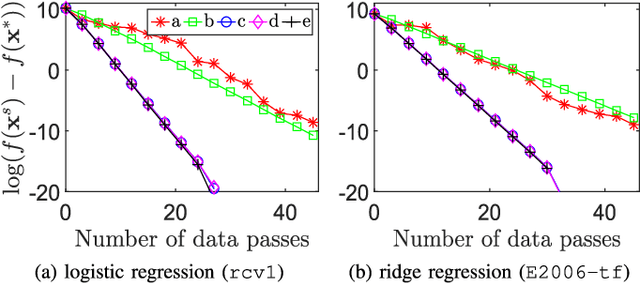
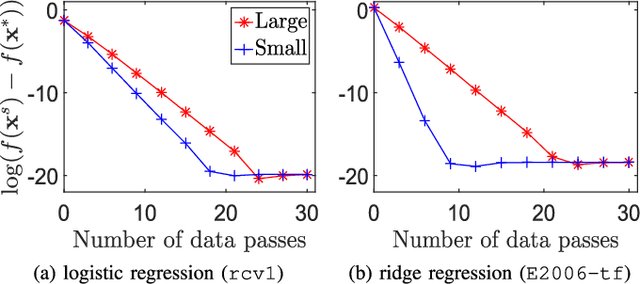
We revisit the stochastic limited-memory BFGS (L-BFGS) algorithm. By proposing a new framework for the convergence analysis, we prove improved convergence rates and computational complexities of the stochastic L-BFGS algorithms compared to previous works. In addition, we propose several practical acceleration strategies to speed up the empirical performance of such algorithms. We also provide theoretical analyses for most of the strategies. Experiments on large-scale logistic and ridge regression problems demonstrate that our proposed strategies yield significant improvements vis-\`a-vis competing state-of-the-art algorithms.

A Unified Framework for Stochastic Matrix Factorization via Variance Reduction

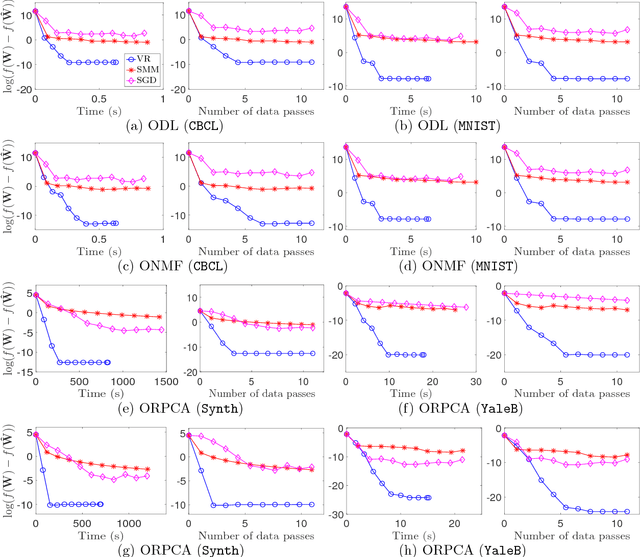
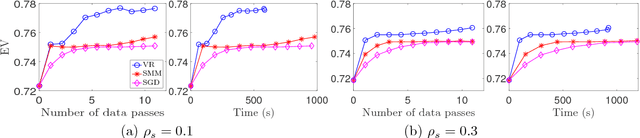
We propose a unified framework to speed up the existing stochastic matrix factorization (SMF) algorithms via variance reduction. Our framework is general and it subsumes several well-known SMF formulations in the literature. We perform a non-asymptotic convergence analysis of our framework and derive computational and sample complexities for our algorithm to converge to an $\epsilon$-stationary point in expectation. In addition, extensive experiments for a wide class of SMF formulations demonstrate that our framework consistently yields faster convergence and a more accurate output dictionary vis-\`a-vis state-of-the-art frameworks.