A Unified Framework for Stochastic Matrix Factorization via Variance Reduction
Paper and Code
May 22, 2017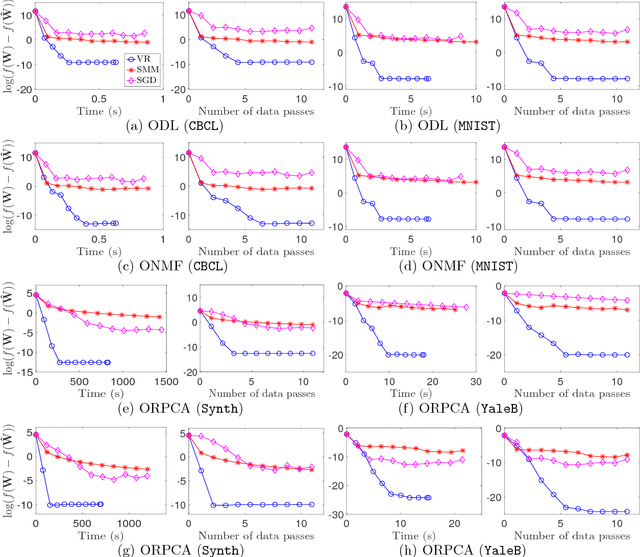
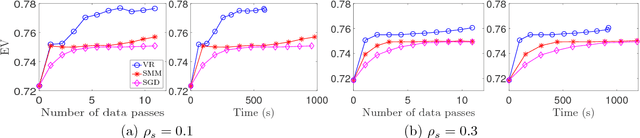
We propose a unified framework to speed up the existing stochastic matrix factorization (SMF) algorithms via variance reduction. Our framework is general and it subsumes several well-known SMF formulations in the literature. We perform a non-asymptotic convergence analysis of our framework and derive computational and sample complexities for our algorithm to converge to an $\epsilon$-stationary point in expectation. In addition, extensive experiments for a wide class of SMF formulations demonstrate that our framework consistently yields faster convergence and a more accurate output dictionary vis-\`a-vis state-of-the-art frameworks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge