Stochastic Approximation for Risk-aware Markov Decision Processes

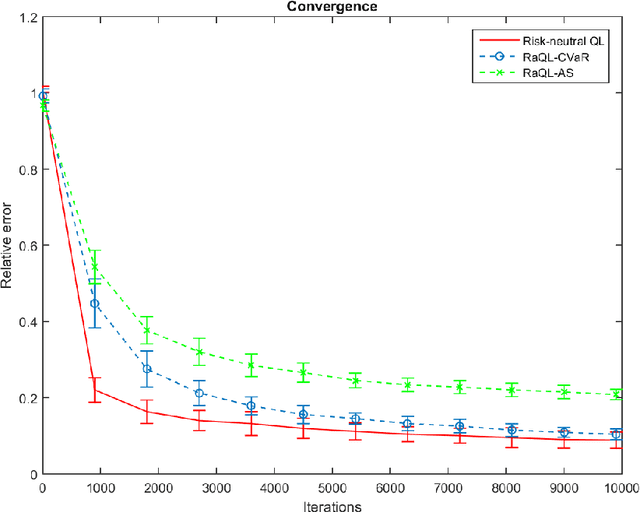
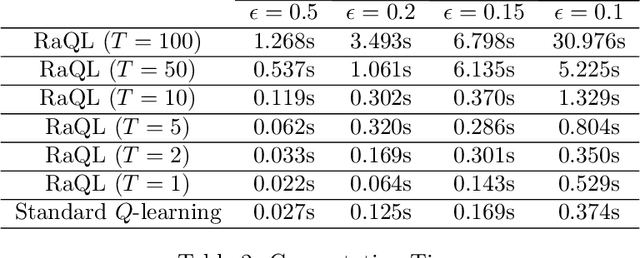
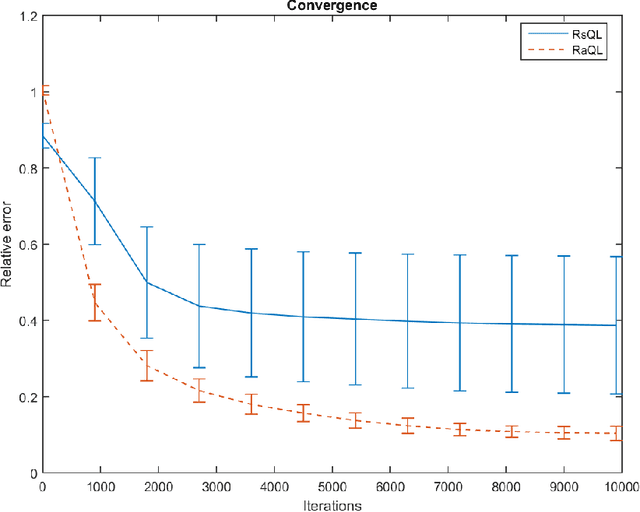
In this paper, we develop a stochastic approximation type algorithm to solve finite state and action, infinite-horizon, risk-aware Markov decision processes. Our algorithm is based on solving stochastic saddle-point problems for risk estimation and doing $Q$-learning for finding the optimal risk-aware policy. We show that several widely investigated risk measures (e.g. conditional value-at-risk, optimized certainty equivalent, and absolute semi-deviation) can be expressed as such stochastic saddle-point problems. We establish the almost sure convergence and convergence rate results for our overall algorithm. For error tolerance $\epsilon$ and learning rate $k$, the convergence rate of our algorithm is $\Omega((\ln(1/\delta\epsilon)/\epsilon^{2})^{1/k}+(\ln(1/\epsilon))^{1/(1-k)})$ with probability $1-\delta$.