Changho Suh
Improving Fair Training under Correlation Shifts
Feb 05, 2023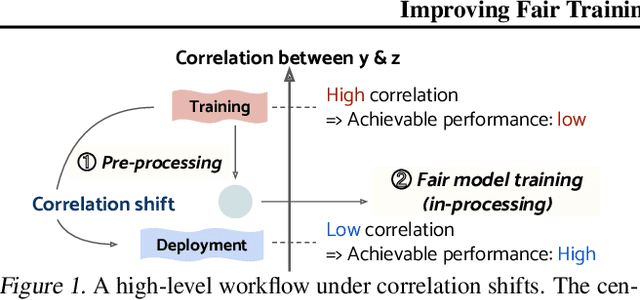
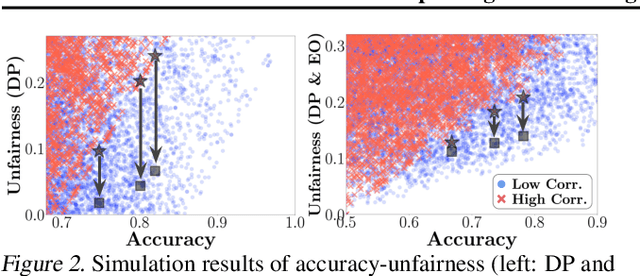
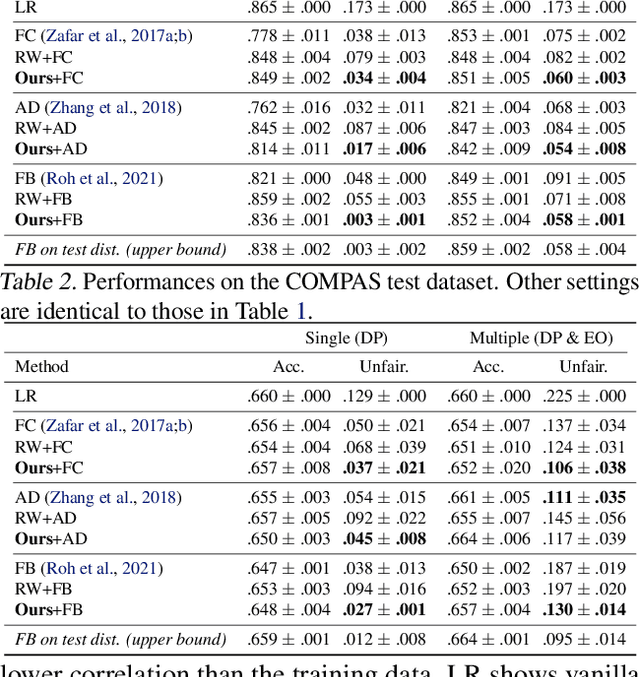
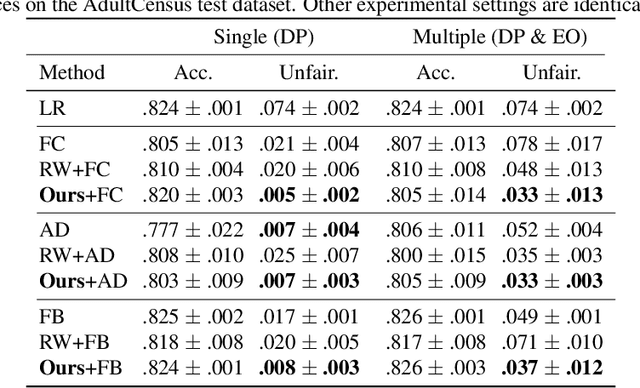
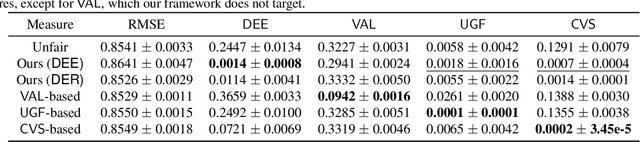
Abstract:Model fairness is an essential element for Trustworthy AI. While many techniques for model fairness have been proposed, most of them assume that the training and deployment data distributions are identical, which is often not true in practice. In particular, when the bias between labels and sensitive groups changes, the fairness of the trained model is directly influenced and can worsen. We make two contributions for solving this problem. First, we analytically show that existing in-processing fair algorithms have fundamental limits in accuracy and group fairness. We introduce the notion of correlation shifts, which can explicitly capture the change of the above bias. Second, we propose a novel pre-processing step that samples the input data to reduce correlation shifts and thus enables the in-processing approaches to overcome their limitations. We formulate an optimization problem for adjusting the data ratio among labels and sensitive groups to reflect the shifted correlation. A key benefit of our approach lies in decoupling the roles of pre- and in-processing approaches: correlation adjustment via pre-processing and unfairness mitigation on the processed data via in-processing. Experiments show that our framework effectively improves existing in-processing fair algorithms w.r.t. accuracy and fairness, both on synthetic and real datasets.
Equal Experience in Recommender Systems
Oct 12, 2022


Abstract:We explore the fairness issue that arises in recommender systems. Biased data due to inherent stereotypes of particular groups (e.g., male students' average rating on mathematics is often higher than that on humanities, and vice versa for females) may yield a limited scope of suggested items to a certain group of users. Our main contribution lies in the introduction of a novel fairness notion (that we call equal experience), which can serve to regulate such unfairness in the presence of biased data. The notion captures the degree of the equal experience of item recommendations across distinct groups. We propose an optimization framework that incorporates the fairness notion as a regularization term, as well as introduce computationally-efficient algorithms that solve the optimization. Experiments on synthetic and benchmark real datasets demonstrate that the proposed framework can indeed mitigate such unfairness while exhibiting a minor degradation of recommendation accuracy.
Matrix Completion with Hierarchical Graph Side Information
Jan 02, 2022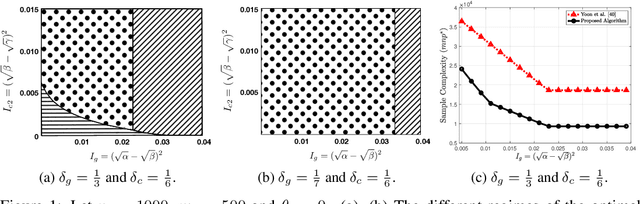


Abstract:We consider a matrix completion problem that exploits social or item similarity graphs as side information. We develop a universal, parameter-free, and computationally efficient algorithm that starts with hierarchical graph clustering and then iteratively refines estimates both on graph clustering and matrix ratings. Under a hierarchical stochastic block model that well respects practically-relevant social graphs and a low-rank rating matrix model (to be detailed), we demonstrate that our algorithm achieves the information-theoretic limit on the number of observed matrix entries (i.e., optimal sample complexity) that is derived by maximum likelihood estimation together with a lower-bound impossibility result. One consequence of this result is that exploiting the hierarchical structure of social graphs yields a substantial gain in sample complexity relative to the one that simply identifies different groups without resorting to the relational structure across them. We conduct extensive experiments both on synthetic and real-world datasets to corroborate our theoretical results as well as to demonstrate significant performance improvements over other matrix completion algorithms that leverage graph side information.
* 53 pages, 3 figures, 1 table. Published in NeurIPS 2020. The first two authors contributed equally to this work. In this revision, achievability proof technique is updated and typos are corrected. arXiv admin note: substantial text overlap with arXiv:2109.05408
Sample Selection for Fair and Robust Training
Oct 27, 2021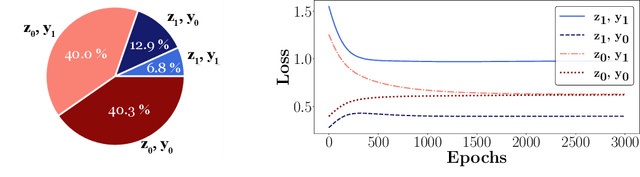
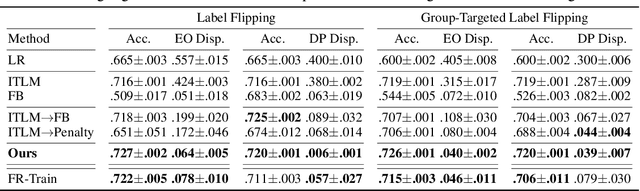
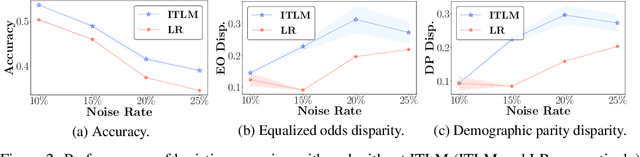
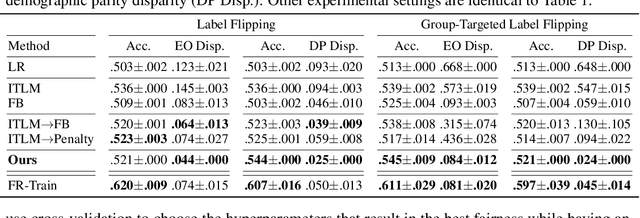
Abstract:Fairness and robustness are critical elements of Trustworthy AI that need to be addressed together. Fairness is about learning an unbiased model while robustness is about learning from corrupted data, and it is known that addressing only one of them may have an adverse affect on the other. In this work, we propose a sample selection-based algorithm for fair and robust training. To this end, we formulate a combinatorial optimization problem for the unbiased selection of samples in the presence of data corruption. Observing that solving this optimization problem is strongly NP-hard, we propose a greedy algorithm that is efficient and effective in practice. Experiments show that our algorithm obtains fairness and robustness that are better than or comparable to the state-of-the-art technique, both on synthetic and benchmark real datasets. Moreover, unlike other fair and robust training baselines, our algorithm can be used by only modifying the sampling step in batch selection without changing the training algorithm or leveraging additional clean data.
On the Fundamental Limits of Matrix Completion: Leveraging Hierarchical Similarity Graphs
Sep 12, 2021



Abstract:We study the matrix completion problem that leverages hierarchical similarity graphs as side information in the context of recommender systems. Under a hierarchical stochastic block model that well respects practically-relevant social graphs and a low-rank rating matrix model, we characterize the exact information-theoretic limit on the number of observed matrix entries (i.e., optimal sample complexity) by proving sharp upper and lower bounds on the sample complexity. In the achievability proof, we demonstrate that probability of error of the maximum likelihood estimator vanishes for sufficiently large number of users and items, if all sufficient conditions are satisfied. On the other hand, the converse (impossibility) proof is based on the genie-aided maximum likelihood estimator. Under each necessary condition, we present examples of a genie-aided estimator to prove that the probability of error does not vanish for sufficiently large number of users and items. One important consequence of this result is that exploiting the hierarchical structure of social graphs yields a substantial gain in sample complexity relative to the one that simply identifies different groups without resorting to the relational structure across them. More specifically, we analyze the optimal sample complexity and identify different regimes whose characteristics rely on quality metrics of side information of the hierarchical similarity graph. Finally, we present simulation results to corroborate our theoretical findings and show that the characterized information-theoretic limit can be asymptotically achieved.
FairBatch: Batch Selection for Model Fairness
Dec 03, 2020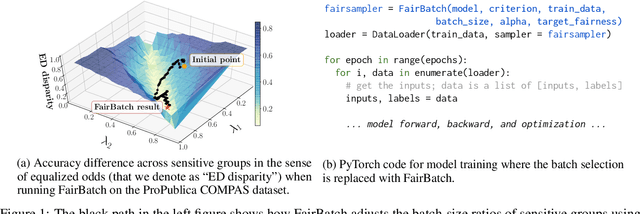
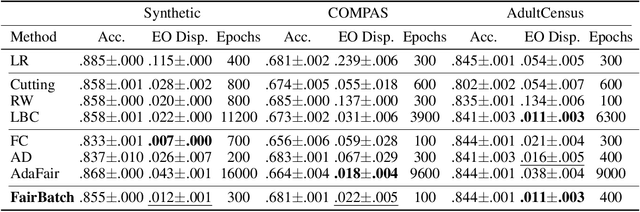
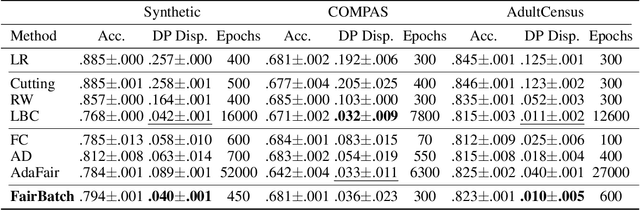
Abstract:Training a fair machine learning model is essential to prevent demographic disparity. Existing techniques for improving model fairness require broad changes in either data preprocessing or model training, rendering themselves difficult-to-adopt for potentially already complex machine learning systems. We address this problem via the lens of bilevel optimization. While keeping the standard training algorithm as an inner optimizer, we incorporate an outer optimizer so as to equip the inner problem with an additional functionality: Adaptively selecting minibatch sizes for the purpose of improving model fairness. Our batch selection algorithm, which we call FairBatch, implements this optimization and supports prominent fairness measures: equal opportunity, equalized odds, and demographic parity. FairBatch comes with a significant implementation benefit -- it does not require any modification to data preprocessing or model training. For instance, a single-line change of PyTorch code for replacing batch selection part of model training suffices to employ FairBatch. Our experiments conducted both on synthetic and benchmark real data demonstrate that FairBatch can provide such functionalities while achieving comparable (or even greater) performances against the state of the arts. Furthermore, FairBatch can readily improve fairness of any pre-trained model simply via fine-tuning. It is also compatible with existing batch selection techniques intended for different purposes, such as faster convergence, thus gracefully achieving multiple purposes.
MC2G: An Efficient Algorithm for Matrix Completion with Social and Item Similarity Graphs
Jun 08, 2020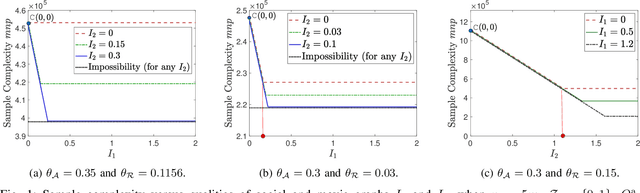
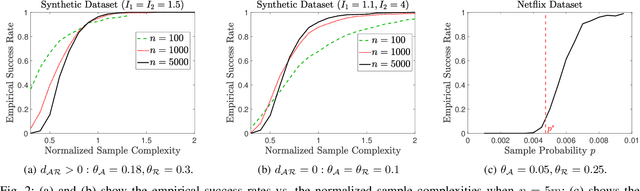
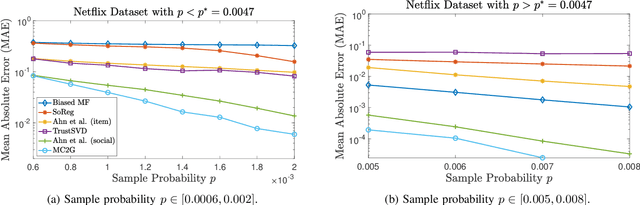
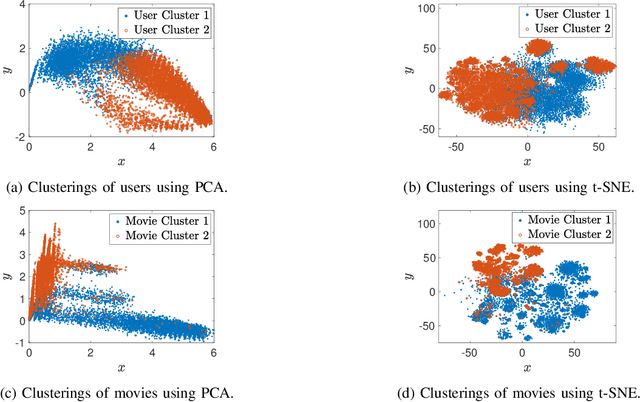
Abstract:We consider a discrete-valued matrix completion problem for recommender systems in which both the social and item similarity graphs are available as side information. We develop and analyze MC2G (Matrix Completion with 2 Graphs), a quasilinear-time algorithm which is based on spectral clustering and local refinement steps. We show that the sample complexity of MC2G meets an information-theoretic limit that is derived using maximum likelihood estimation and is also order-optimal. We demonstrate that having both graphs as side information outperforms having just a single graph, thus the availability of two graphs results in a synergistic effect. Experiments on synthetic datasets corroborate our theoretical results. Finally, experiments on a sub-sampled version of the Netflix dataset show that MC2G significantly outperforms other state-of-the-art matrix completion algorithms that leverage graph side information.
FR-Train: A mutual information-based approach to fair and robust training
Feb 24, 2020
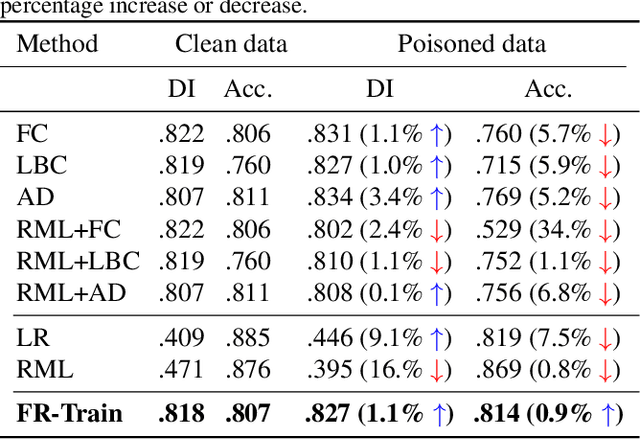
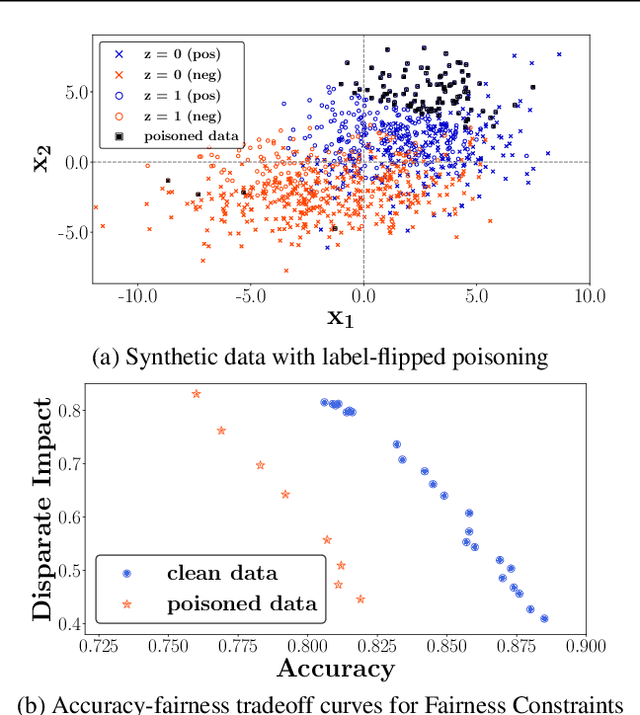
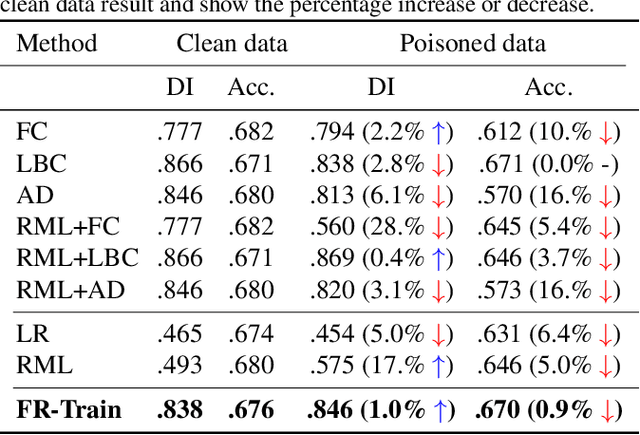
Abstract:Trustworthy AI is a critical issue in machine learning where, in addition to training a model that is accurate, one must consider both fair and robust training in the presence of data bias and poisoning. However, the existing model fairness techniques mistakenly view poisoned data as an additional bias, resulting in severe performance degradation. To fix this problem, we propose FR-Train, which holistically performs fair and robust model training. We provide a mutual information-based interpretation of an existing adversarial training-based fairness-only method, and apply this idea to architect an additional discriminator that can identify poisoned data using a clean validation set and reduce its influence. In our experiments, FR-Train shows almost no decrease in fairness and accuracy in the presence of data poisoning by both mitigating the bias and defending against poisoning. We also demonstrate how to construct clean validation sets using crowdsourcing, and release new benchmark datasets.
Community Detection and Matrix Completion with Two-Sided Graph Side-Information
Dec 06, 2019



Abstract:We consider the problem of recovering communities of users and communities of items (such as movies) based on a partially observed rating matrix as well as side-information in the form of similarity graphs of the users and items. The user-to-user and item-to-item similarity graphs are generated according to the celebrated stochastic block model (SBM). We develop lower and upper bounds on the minimum expected number of observed ratings (also known as the sample complexity) needed for this recovery task. These bounds are functions of various parameters including the quality of the graph side-information which is manifested in the intra- and inter-cluster probabilities of the SBMs. We show that these bounds match for a wide range of parameters of interest, and match up to a constant factor of two for the remaining parameter regime. Our information-theoretic results quantify the benefits of the two-sided graph side-information for recovery, and further analysis reveals that the two pieces of graph side-information produce an interesting synergistic effect under certain scenarios. This means that if one observes only one of the two graphs, then the required sample complexity worsens to the case in which none of the graphs is observed. Thus both graphs are strictly needed to reduce the sample complexity.
Wasserstein GAN Can Perform PCA
Feb 25, 2019



Abstract:Generative Adversarial Networks (GANs) have become a powerful framework to learn generative models that arise across a wide variety of domains. While there has been a recent surge in the development of numerous GAN architectures with distinct optimization metrics, we are still lacking in our understanding on how far away such GANs are from optimality. In this paper, we make progress on a theoretical understanding of the GANs under a simple linear-generator Gaussian-data setting where the optimal maximum-likelihood generator is known to perform Principal Component Analysis (PCA). We find that the original GAN by Goodfellow et. al. fails to recover the optimal PCA solution. On the other hand, we show that Wasserstein GAN can perform PCA, and hence it may serve as a basis for an optimal GAN architecture that yields the optimal generator for a wide range of data settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge