MC2G: An Efficient Algorithm for Matrix Completion with Social and Item Similarity Graphs

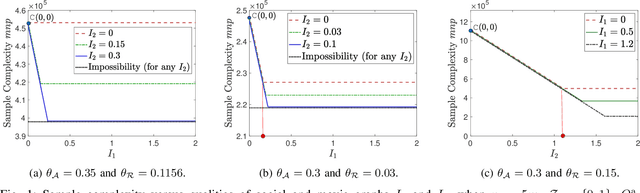
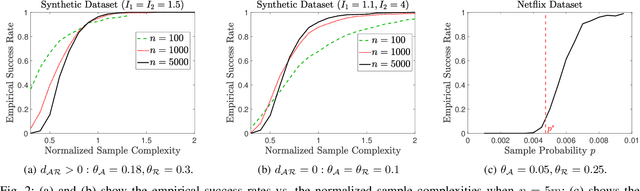
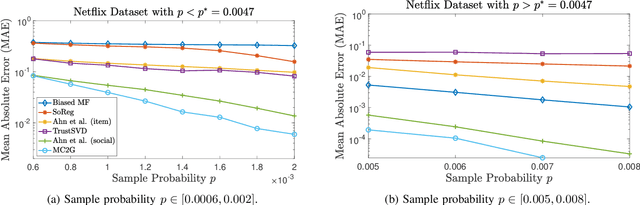
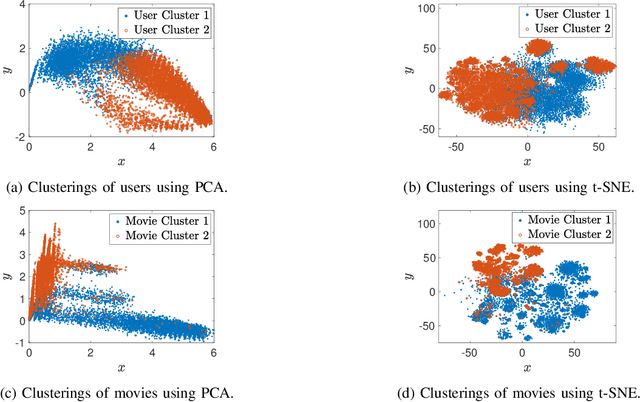
We consider a discrete-valued matrix completion problem for recommender systems in which both the social and item similarity graphs are available as side information. We develop and analyze MC2G (Matrix Completion with 2 Graphs), a quasilinear-time algorithm which is based on spectral clustering and local refinement steps. We show that the sample complexity of MC2G meets an information-theoretic limit that is derived using maximum likelihood estimation and is also order-optimal. We demonstrate that having both graphs as side information outperforms having just a single graph, thus the availability of two graphs results in a synergistic effect. Experiments on synthetic datasets corroborate our theoretical results. Finally, experiments on a sub-sampled version of the Netflix dataset show that MC2G significantly outperforms other state-of-the-art matrix completion algorithms that leverage graph side information.