Soheil Mohajer
Matrix Completion with Hierarchical Graph Side Information
Jan 02, 2022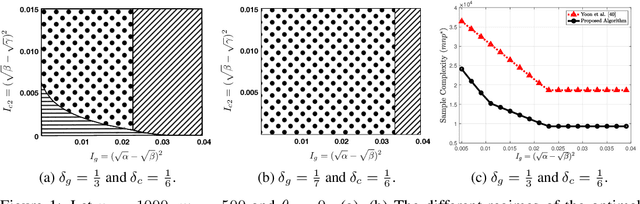


Abstract:We consider a matrix completion problem that exploits social or item similarity graphs as side information. We develop a universal, parameter-free, and computationally efficient algorithm that starts with hierarchical graph clustering and then iteratively refines estimates both on graph clustering and matrix ratings. Under a hierarchical stochastic block model that well respects practically-relevant social graphs and a low-rank rating matrix model (to be detailed), we demonstrate that our algorithm achieves the information-theoretic limit on the number of observed matrix entries (i.e., optimal sample complexity) that is derived by maximum likelihood estimation together with a lower-bound impossibility result. One consequence of this result is that exploiting the hierarchical structure of social graphs yields a substantial gain in sample complexity relative to the one that simply identifies different groups without resorting to the relational structure across them. We conduct extensive experiments both on synthetic and real-world datasets to corroborate our theoretical results as well as to demonstrate significant performance improvements over other matrix completion algorithms that leverage graph side information.
* 53 pages, 3 figures, 1 table. Published in NeurIPS 2020. The first two authors contributed equally to this work. In this revision, achievability proof technique is updated and typos are corrected. arXiv admin note: substantial text overlap with arXiv:2109.05408
On the Fundamental Limits of Matrix Completion: Leveraging Hierarchical Similarity Graphs
Sep 12, 2021



Abstract:We study the matrix completion problem that leverages hierarchical similarity graphs as side information in the context of recommender systems. Under a hierarchical stochastic block model that well respects practically-relevant social graphs and a low-rank rating matrix model, we characterize the exact information-theoretic limit on the number of observed matrix entries (i.e., optimal sample complexity) by proving sharp upper and lower bounds on the sample complexity. In the achievability proof, we demonstrate that probability of error of the maximum likelihood estimator vanishes for sufficiently large number of users and items, if all sufficient conditions are satisfied. On the other hand, the converse (impossibility) proof is based on the genie-aided maximum likelihood estimator. Under each necessary condition, we present examples of a genie-aided estimator to prove that the probability of error does not vanish for sufficiently large number of users and items. One important consequence of this result is that exploiting the hierarchical structure of social graphs yields a substantial gain in sample complexity relative to the one that simply identifies different groups without resorting to the relational structure across them. More specifically, we analyze the optimal sample complexity and identify different regimes whose characteristics rely on quality metrics of side information of the hierarchical similarity graph. Finally, we present simulation results to corroborate our theoretical findings and show that the characterized information-theoretic limit can be asymptotically achieved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge