Synergistic Approach for Simultaneous Optimization of Monolingual, Cross-lingual, and Multilingual Information Retrieval

Information retrieval across different languages is an increasingly important challenge in natural language processing. Recent approaches based on multilingual pre-trained language models have achieved remarkable success, yet they often optimize for either monolingual, cross-lingual, or multilingual retrieval performance at the expense of others. This paper proposes a novel hybrid batch training strategy to simultaneously improve zero-shot retrieval performance across monolingual, cross-lingual, and multilingual settings while mitigating language bias. The approach fine-tunes multilingual language models using a mix of monolingual and cross-lingual question-answer pair batches sampled based on dataset size. Experiments on XQuAD-R, MLQA-R, and MIRACL benchmark datasets show that the proposed method consistently achieves comparable or superior results in zero-shot retrieval across various languages and retrieval tasks compared to monolingual-only or cross-lingual-only training. Hybrid batch training also substantially reduces language bias in multilingual retrieval compared to monolingual training. These results demonstrate the effectiveness of the proposed approach for learning language-agnostic representations that enable strong zero-shot retrieval performance across diverse languages.

Deconstructing Classifiers: Towards A Data Reconstruction Attack Against Text Classification Models

Natural language processing (NLP) models have become increasingly popular in real-world applications, such as text classification. However, they are vulnerable to privacy attacks, including data reconstruction attacks that aim to extract the data used to train the model. Most previous studies on data reconstruction attacks have focused on LLM, while classification models were assumed to be more secure. In this work, we propose a new targeted data reconstruction attack called the Mix And Match attack, which takes advantage of the fact that most classification models are based on LLM. The Mix And Match attack uses the base model of the target model to generate candidate tokens and then prunes them using the classification head. We extensively demonstrate the effectiveness of the attack using both random and organic canaries. This work highlights the importance of considering the privacy risks associated with data reconstruction attacks in classification models and offers insights into possible leakages.

Privacy Leakage in Text Classification: A Data Extraction Approach

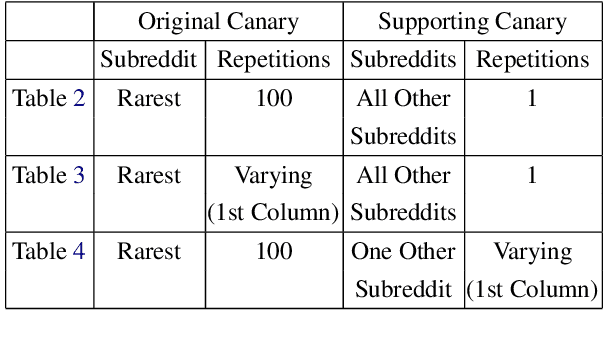
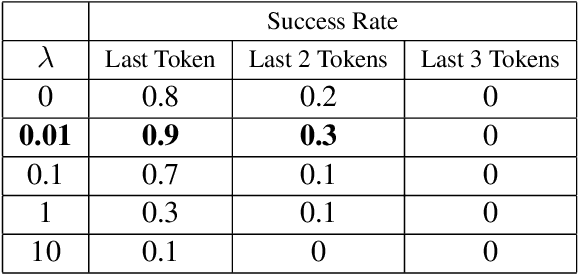
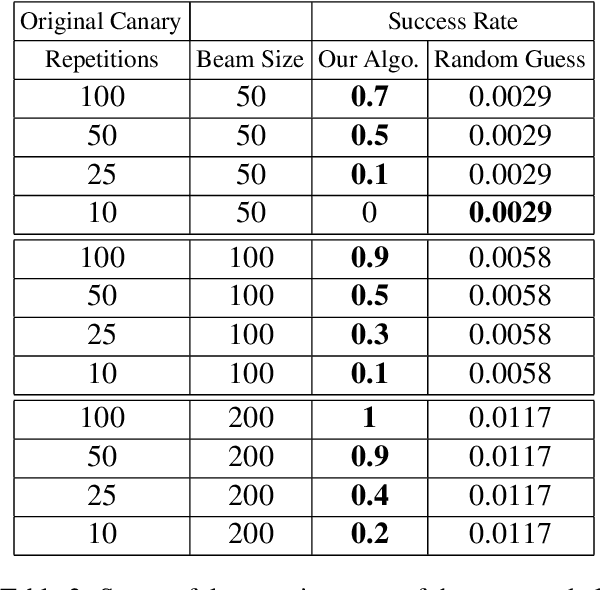
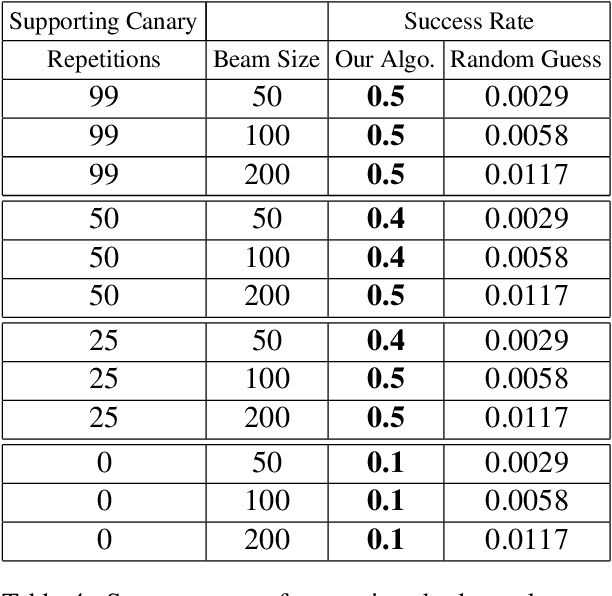
Recent work has demonstrated the successful extraction of training data from generative language models. However, it is not evident whether such extraction is feasible in text classification models since the training objective is to predict the class label as opposed to next-word prediction. This poses an interesting challenge and raises an important question regarding the privacy of training data in text classification settings. Therefore, we study the potential privacy leakage in the text classification domain by investigating the problem of unintended memorization of training data that is not pertinent to the learning task. We propose an algorithm to extract missing tokens of a partial text by exploiting the likelihood of the class label provided by the model. We test the effectiveness of our algorithm by inserting canaries into the training set and attempting to extract tokens in these canaries post-training. In our experiments, we demonstrate that successful extraction is possible to some extent. This can also be used as an auditing strategy to assess any potential unauthorized use of personal data without consent.

Matrix Completion with Hierarchical Graph Side Information

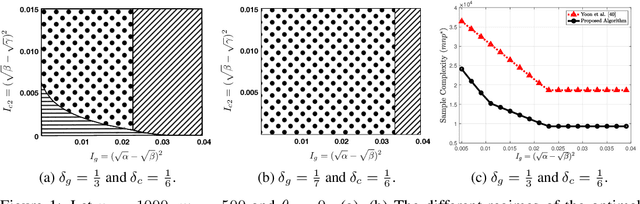
We consider a matrix completion problem that exploits social or item similarity graphs as side information. We develop a universal, parameter-free, and computationally efficient algorithm that starts with hierarchical graph clustering and then iteratively refines estimates both on graph clustering and matrix ratings. Under a hierarchical stochastic block model that well respects practically-relevant social graphs and a low-rank rating matrix model (to be detailed), we demonstrate that our algorithm achieves the information-theoretic limit on the number of observed matrix entries (i.e., optimal sample complexity) that is derived by maximum likelihood estimation together with a lower-bound impossibility result. One consequence of this result is that exploiting the hierarchical structure of social graphs yields a substantial gain in sample complexity relative to the one that simply identifies different groups without resorting to the relational structure across them. We conduct extensive experiments both on synthetic and real-world datasets to corroborate our theoretical results as well as to demonstrate significant performance improvements over other matrix completion algorithms that leverage graph side information.

On the Fundamental Limits of Matrix Completion: Leveraging Hierarchical Similarity Graphs

We study the matrix completion problem that leverages hierarchical similarity graphs as side information in the context of recommender systems. Under a hierarchical stochastic block model that well respects practically-relevant social graphs and a low-rank rating matrix model, we characterize the exact information-theoretic limit on the number of observed matrix entries (i.e., optimal sample complexity) by proving sharp upper and lower bounds on the sample complexity. In the achievability proof, we demonstrate that probability of error of the maximum likelihood estimator vanishes for sufficiently large number of users and items, if all sufficient conditions are satisfied. On the other hand, the converse (impossibility) proof is based on the genie-aided maximum likelihood estimator. Under each necessary condition, we present examples of a genie-aided estimator to prove that the probability of error does not vanish for sufficiently large number of users and items. One important consequence of this result is that exploiting the hierarchical structure of social graphs yields a substantial gain in sample complexity relative to the one that simply identifies different groups without resorting to the relational structure across them. More specifically, we analyze the optimal sample complexity and identify different regimes whose characteristics rely on quality metrics of side information of the hierarchical similarity graph. Finally, we present simulation results to corroborate our theoretical findings and show that the characterized information-theoretic limit can be asymptotically achieved.