Adversarial Top-$K$ Ranking
Paper and Code
Feb 15, 2016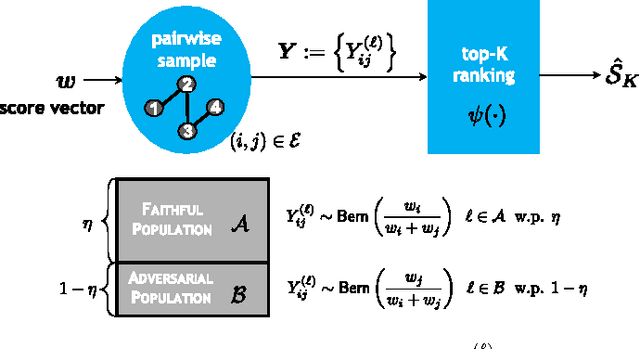
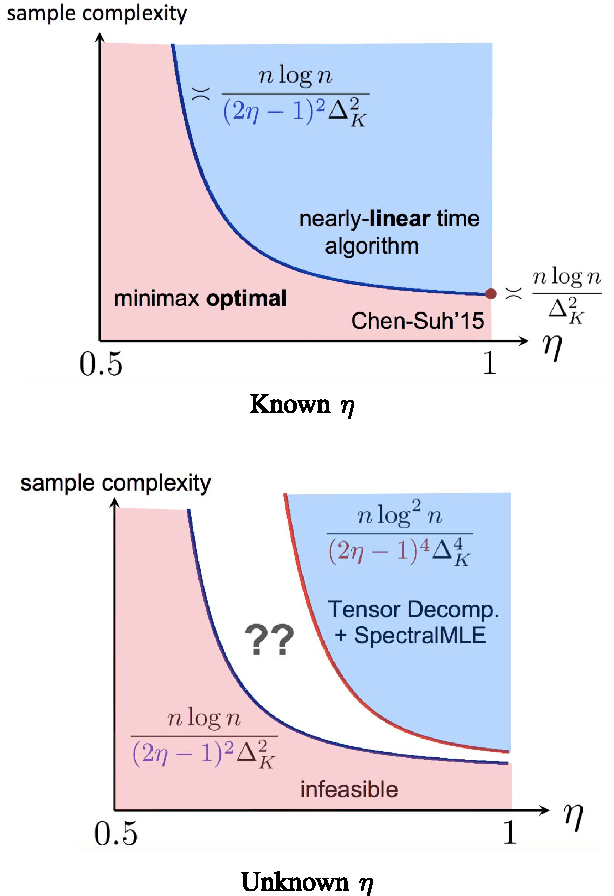
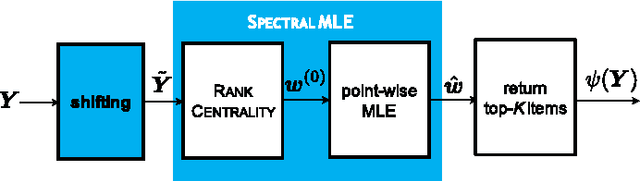
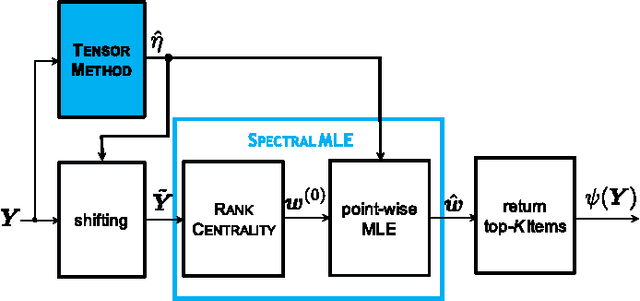
We study the top-$K$ ranking problem where the goal is to recover the set of top-$K$ ranked items out of a large collection of items based on partially revealed preferences. We consider an adversarial crowdsourced setting where there are two population sets, and pairwise comparison samples drawn from one of the populations follow the standard Bradley-Terry-Luce model (i.e., the chance of item $i$ beating item $j$ is proportional to the relative score of item $i$ to item $j$), while in the other population, the corresponding chance is inversely proportional to the relative score. When the relative size of the two populations is known, we characterize the minimax limit on the sample size required (up to a constant) for reliably identifying the top-$K$ items, and demonstrate how it scales with the relative size. Moreover, by leveraging a tensor decomposition method for disambiguating mixture distributions, we extend our result to the more realistic scenario in which the relative population size is unknown, thus establishing an upper bound on the fundamental limit of the sample size for recovering the top-$K$ set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge