Online Nonnegative Matrix Factorization with General Divergences
Paper and Code
Aug 02, 2016
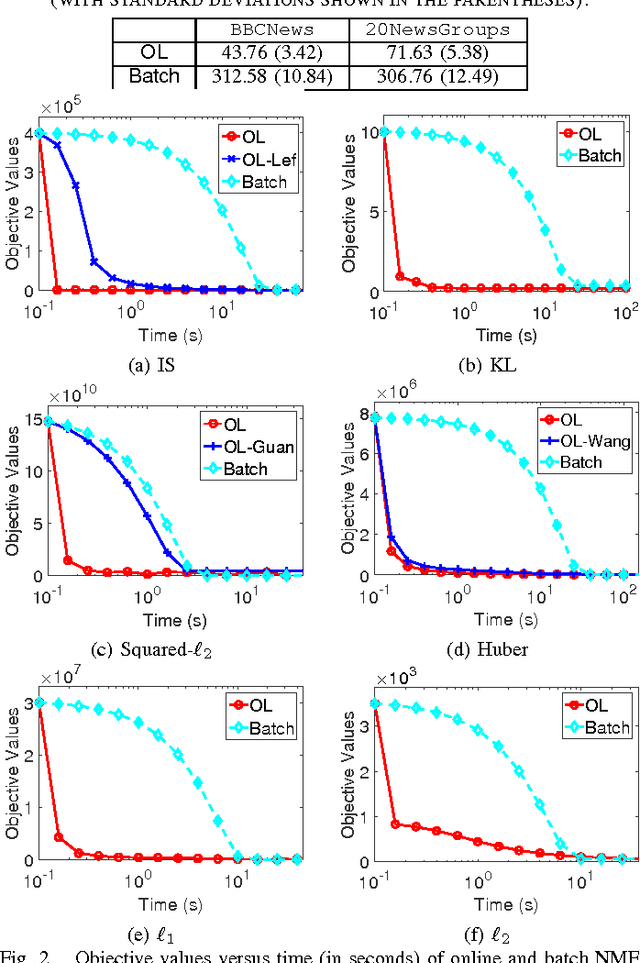


We develop a unified and systematic framework for performing online nonnegative matrix factorization under a wide variety of important divergences. The online nature of our algorithm makes it particularly amenable to large-scale data. We prove that the sequence of learned dictionaries converges almost surely to the set of critical points of the expected loss function. We do so by leveraging the theory of stochastic approximations and projected dynamical systems. This result substantially generalizes the previous results obtained only for the squared-$\ell_2$ loss. Moreover, the novel techniques involved in our analysis open new avenues for analyzing similar matrix factorization problems. The computational efficiency and the quality of the learned dictionary of our algorithm are verified empirically on both synthetic and real datasets. In particular, on the tasks of topic learning, shadow removal and image denoising, our algorithm achieves superior trade-offs between the quality of learned dictionary and running time over the batch and other online NMF algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge