Online Nonnegative Matrix Factorization with Outliers
Paper and Code
Oct 15, 2016

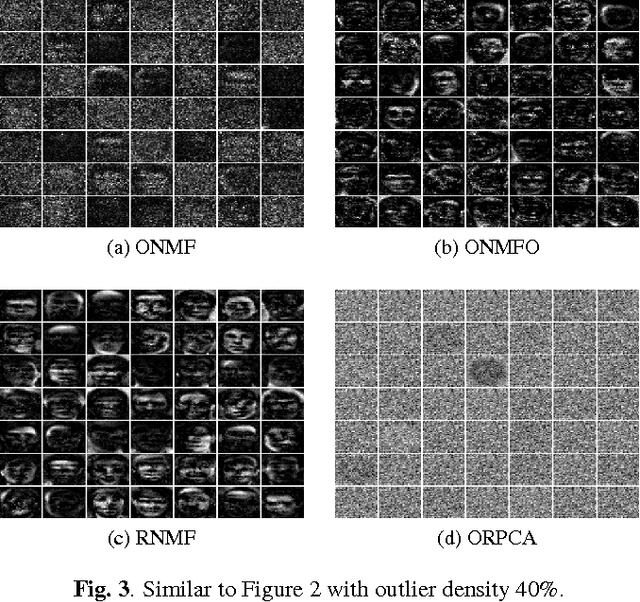
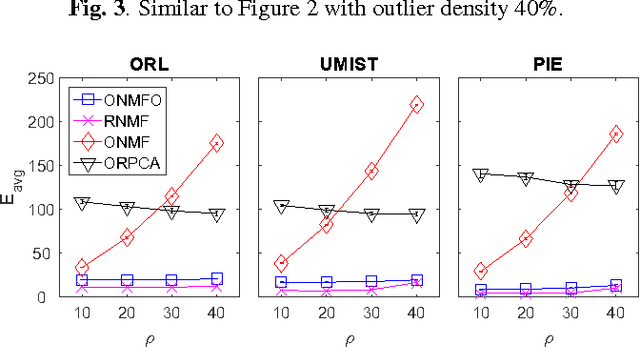
We propose a unified and systematic framework for performing online nonnegative matrix factorization in the presence of outliers. Our framework is particularly suited to large-scale data. We propose two solvers based on projected gradient descent and the alternating direction method of multipliers. We prove that the sequence of objective values converges almost surely by appealing to the quasi-martingale convergence theorem. We also show the sequence of learned dictionaries converges to the set of stationary points of the expected loss function almost surely. In addition, we extend our basic problem formulation to various settings with different constraints and regularizers. We also adapt the solvers and analyses to each setting. We perform extensive experiments on both synthetic and real datasets. These experiments demonstrate the computational efficiency and efficacy of our algorithms on tasks such as (parts-based) basis learning, image denoising, shadow removal and foreground-background separation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge