Brain-inspired AI Agent: The Way Towards AGI

Artificial General Intelligence (AGI), widely regarded as the fundamental goal of artificial intelligence, represents the realization of cognitive capabilities that enable the handling of general tasks with human-like proficiency. Researchers in brain-inspired AI seek inspiration from the operational mechanisms of the human brain, aiming to replicate its functional rules in intelligent models. Moreover, with the rapid development of large-scale models in recent years, the concept of agents has garnered increasing attention, with researchers widely recognizing it as a necessary pathway toward achieving AGI. In this article, we propose the concept of a brain-inspired AI agent and analyze how to extract relatively feasible and agent-compatible cortical region functionalities and their associated functional connectivity networks from the complex mechanisms of the human brain. Implementing these structures within an agent enables it to achieve basic cognitive intelligence akin to human capabilities. Finally, we explore the limitations and challenges for realizing brain-inspired agents and discuss their future development.

Evaluating the design space of diffusion-based generative models

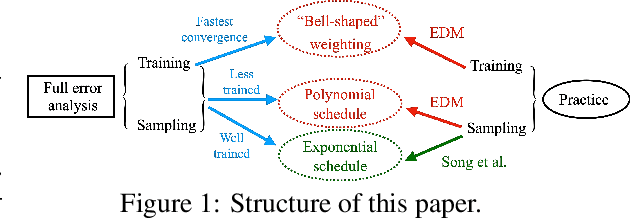
Most existing theoretical investigations of the accuracy of diffusion models, albeit significant, assume the score function has been approximated to a certain accuracy, and then use this a priori bound to control the error of generation. This article instead provides a first quantitative understanding of the whole generation process, i.e., both training and sampling. More precisely, it conducts a non-asymptotic convergence analysis of denoising score matching under gradient descent. In addition, a refined sampling error analysis for variance exploding models is also provided. The combination of these two results yields a full error analysis, which elucidates (again, but this time theoretically) how to design the training and sampling processes for effective generation. For instance, our theory implies a preference toward noise distribution and loss weighting that qualitatively agree with the ones used in [Karras et al. 2022]. It also provides some perspectives on why the time and variance schedule used in [Karras et al. 2022] could be better tuned than the pioneering version in [Song et al. 2020].

A Separation in Heavy-Tailed Sampling: Gaussian vs. Stable Oracles for Proximal Samplers

We study the complexity of heavy-tailed sampling and present a separation result in terms of obtaining high-accuracy versus low-accuracy guarantees i.e., samplers that require only $O(\log(1/\varepsilon))$ versus $\Omega(\text{poly}(1/\varepsilon))$ iterations to output a sample which is $\varepsilon$-close to the target in $\chi^2$-divergence. Our results are presented for proximal samplers that are based on Gaussian versus stable oracles. We show that proximal samplers based on the Gaussian oracle have a fundamental barrier in that they necessarily achieve only low-accuracy guarantees when sampling from a class of heavy-tailed targets. In contrast, proximal samplers based on the stable oracle exhibit high-accuracy guarantees, thereby overcoming the aforementioned limitation. We also prove lower bounds for samplers under the stable oracle and show that our upper bounds cannot be fundamentally improved.

Zeroth-Order Sampling Methods for Non-Log-Concave Distributions: Alleviating Metastability by Denoising Diffusion

This paper considers the problem of sampling from non-logconcave distribution, based on queries of its unnormalized density. It first describes a framework, Diffusion Monte Carlo (DMC), based on the simulation of a denoising diffusion process with its score function approximated by a generic Monte Carlo estimator. DMC is an oracle-based meta-algorithm, where its oracle is the assumed access to samples that generate a Monte Carlo score estimator. Then we provide an implementation of this oracle, based on rejection sampling, and this turns DMC into a true algorithm, termed Zeroth-Order Diffusion Monte Carlo (ZOD-MC). We provide convergence analyses by first constructing a general framework, i.e. a performance guarantee for DMC, without assuming the target distribution to be log-concave or satisfying any isoperimetric inequality. Then we prove that ZOD-MC admits an inverse polynomial dependence on the desired sampling accuracy, albeit still suffering from the curse of dimensionality. Consequently, for low dimensional distributions, ZOD-MC is a very efficient sampler, with performance exceeding latest samplers, including also-denoising-diffusion-based RDMC and RS-DMC. Last, we experimentally demonstrate the insensitivity of ZOD-MC to increasingly higher barriers between modes or discontinuity in non-convex potential.

High-dimensional scaling limits and fluctuations of online least-squares SGD with smooth covariance

We derive high-dimensional scaling limits and fluctuations for the online least-squares Stochastic Gradient Descent (SGD) algorithm by taking the properties of the data generating model explicitly into consideration. Our approach treats the SGD iterates as an interacting particle system, where the expected interaction is characterized by the covariance structure of the input. Assuming smoothness conditions on moments of order up to eight orders, and without explicitly assuming Gaussianity, we establish the high-dimensional scaling limits and fluctuations in the form of infinite-dimensional Ordinary Differential Equations (ODEs) or Stochastic Differential Equations (SDEs). Our results reveal a precise three-step phase transition of the iterates; it goes from being ballistic, to diffusive, and finally to purely random behavior, as the noise variance goes from low, to moderate and finally to very-high noise setting. In the low-noise setting, we further characterize the precise fluctuations of the (scaled) iterates as infinite-dimensional SDEs. We also show the existence and uniqueness of solutions to the derived limiting ODEs and SDEs. Our results have several applications, including characterization of the limiting mean-square estimation or prediction errors and their fluctuations which can be obtained by analytically or numerically solving the limiting equations.

Towards a Complete Analysis of Langevin Monte Carlo: Beyond Poincaré Inequality

Langevin diffusions are rapidly convergent under appropriate functional inequality assumptions. Hence, it is natural to expect that with additional smoothness conditions to handle the discretization errors, their discretizations like the Langevin Monte Carlo (LMC) converge in a similar fashion. This research program was initiated by Vemapala and Wibisono (2019), who established results under log-Sobolev inequalities. Chewi et al. (2022) extended the results to handle the case of Poincar\'e inequalities. In this paper, we go beyond Poincar\'e inequalities, and push this research program to its limit. We do so by establishing upper and lower bounds for Langevin diffusions and LMC under weak Poincar\'e inequalities that are satisfied by a large class of densities including polynomially-decaying heavy-tailed densities (i.e., Cauchy-type). Our results explicitly quantify the effect of the initializer on the performance of the LMC algorithm. In particular, we show that as the tail goes from sub-Gaussian, to sub-exponential, and finally to Cauchy-like, the dependency on the initial error goes from being logarithmic, to polynomial, and then finally to being exponential. This three-step phase transition is in particular unavoidable as demonstrated by our lower bounds, clearly defining the boundaries of LMC.

Mean-Square Analysis of Discretized Itô Diffusions for Heavy-tailed Sampling

We analyze the complexity of sampling from a class of heavy-tailed distributions by discretizing a natural class of It\^o diffusions associated with weighted Poincar\'e inequalities. Based on a mean-square analysis, we establish the iteration complexity for obtaining a sample whose distribution is $\epsilon$ close to the target distribution in the Wasserstein-2 metric. In this paper, our results take the mean-square analysis to its limits, i.e., we invariably only require that the target density has finite variance, the minimal requirement for a mean-square analysis. To obtain explicit estimates, we compute upper bounds on certain moments associated with heavy-tailed targets under various assumptions. We also provide similar iteration complexity results for the case where only function evaluations of the unnormalized target density are available by estimating the gradients using a Gaussian smoothing technique. We provide illustrative examples based on the multivariate $t$-distribution.

Regularized Stein Variational Gradient Flow

The Stein Variational Gradient Descent (SVGD) algorithm is an deterministic particle method for sampling. However, a mean-field analysis reveals that the gradient flow corresponding to the SVGD algorithm (i.e., the Stein Variational Gradient Flow) only provides a constant-order approximation to the Wasserstein Gradient Flow corresponding to the KL-divergence minimization. In this work, we propose the Regularized Stein Variational Gradient Flow which interpolates between the Stein Variational Gradient Flow and the Wasserstein Gradient Flow. We establish various theoretical properties of the Regularized Stein Variational Gradient Flow (and its time-discretization) including convergence to equilibrium, existence and uniqueness of weak solutions, and stability of the solutions. We provide preliminary numerical evidence of the improved performance offered by the regularization.

Heavy-tailed Sampling via Transformed Unadjusted Langevin Algorithm

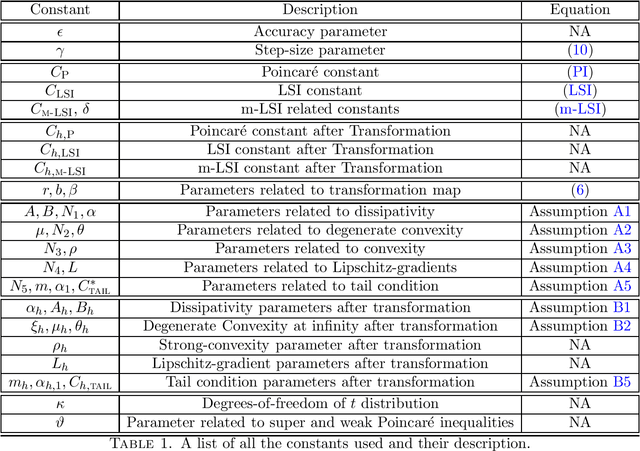
We analyze the oracle complexity of sampling from polynomially decaying heavy-tailed target densities based on running the Unadjusted Langevin Algorithm on certain transformed versions of the target density. The specific class of closed-form transformation maps that we construct are shown to be diffeomorphisms, and are particularly suited for developing efficient diffusion-based samplers. We characterize the precise class of heavy-tailed densities for which polynomial-order oracle complexities (in dimension and inverse target accuracy) could be obtained, and provide illustrative examples. We highlight the relationship between our assumptions and functional inequalities (super and weak Poincar\'e inequalities) based on non-local Dirichlet forms defined via fractional Laplacian operators, used to characterize the heavy-tailed equilibrium densities of certain stable-driven stochastic differential equations.

On the Ergodicity, Bias and Asymptotic Normality of Randomized Midpoint Sampling Method

The randomized midpoint method, proposed by [SL19], has emerged as an optimal discretization procedure for simulating the continuous time Langevin diffusions. Focusing on the case of strong-convex and smooth potentials, in this paper, we analyze several probabilistic properties of the randomized midpoint discretization method for both overdamped and underdamped Langevin diffusions. We first characterize the stationary distribution of the discrete chain obtained with constant step-size discretization and show that it is biased away from the target distribution. Notably, the step-size needs to go to zero to obtain asymptotic unbiasedness. Next, we establish the asymptotic normality for numerical integration using the randomized midpoint method and highlight the relative advantages and disadvantages over other discretizations. Our results collectively provide several insights into the behavior of the randomized midpoint discretization method, including obtaining confidence intervals for numerical integrations.