Multivariate Gaussian Approximation for Random Forest via Region-based Stabilization

We derive Gaussian approximation bounds for random forest predictions based on a set of training points given by a Poisson process, under fairly mild regularity assumptions on the data generating process. Our approach is based on the key observation that the random forest predictions satisfy a certain geometric property called region-based stabilization. In the process of developing our results for the random forest, we also establish a probabilistic result, which might be of independent interest, on multivariate Gaussian approximation bounds for general functionals of Poisson process that are region-based stabilizing. This general result makes use of the Malliavin-Stein method, and is potentially applicable to various related statistical problems.

Nonsmooth Nonparametric Regression via Fractional Laplacian Eigenmaps

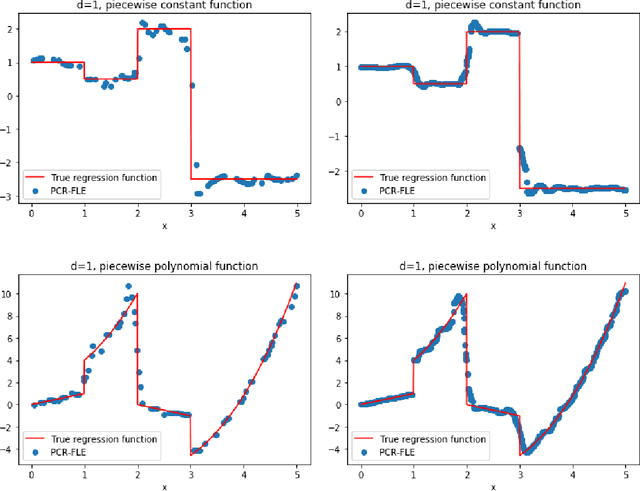
We develop nonparametric regression methods for the case when the true regression function is not necessarily smooth. More specifically, our approach is using the fractional Laplacian and is designed to handle the case when the true regression function lies in an $L_2$-fractional Sobolev space with order $s\in (0,1)$. This function class is a Hilbert space lying between the space of square-integrable functions and the first-order Sobolev space consisting of differentiable functions. It contains fractional power functions, piecewise constant or polynomial functions and bump function as canonical examples. For the proposed approach, we prove upper bounds on the in-sample mean-squared estimation error of order $n^{-\frac{2s}{2s+d}}$, where $d$ is the dimension, $s$ is the aforementioned order parameter and $n$ is the number of observations. We also provide preliminary empirical results validating the practical performance of the developed estimators.

Adaptive and non-adaptive minimax rates for weighted Laplacian-eigenmap based nonparametric regression

We show both adaptive and non-adaptive minimax rates of convergence for a family of weighted Laplacian-Eigenmap based nonparametric regression methods, when the true regression function belongs to a Sobolev space and the sampling density is bounded from above and below. The adaptation methodology is based on extensions of Lepski's method and is over both the smoothness parameter ($s\in\mathbb{N}_{+}$) and the norm parameter ($M>0$) determining the constraints on the Sobolev space. Our results extend the non-adaptive result in \cite{green2021minimax}, established for a specific normalized graph Laplacian, to a wide class of weighted Laplacian matrices used in practice, including the unnormalized Laplacian and random walk Laplacian.

A Flexible Approach for Normal Approximation of Geometric and Topological Statistics

We derive normal approximation results for a class of stabilizing functionals of binomial or Poisson point process, that are not necessarily expressible as sums of certain score functions. Our approach is based on a flexible notion of the add-one cost operator, which helps one to deal with the second-order cost operator via suitably appropriate first-order operators. We combine this flexible notion with the theory of strong stabilization to establish our results. We illustrate the applicability of our results by establishing normal approximation results for certain geometric and topological statistics arising frequently in practice. Several existing results also emerge as special cases of our approach.

Topologically penalized regression on manifolds

We study a regression problem on a compact manifold M. In order to take advantage of the underlying geometry and topology of the data, the regression task is performed on the basis of the first several eigenfunctions of the Laplace-Beltrami operator of the manifold, that are regularized with topological penalties. The proposed penalties are based on the topology of the sub-level sets of either the eigenfunctions or the estimated function. The overall approach is shown to yield promising and competitive performance on various applications to both synthetic and real data sets. We also provide theoretical guarantees on the regression function estimates, on both its prediction error and its smoothness (in a topological sense). Taken together, these results support the relevance of our approach in the case where the targeted function is "topologically smooth".

Algorithms for ridge estimation with convergence guarantees

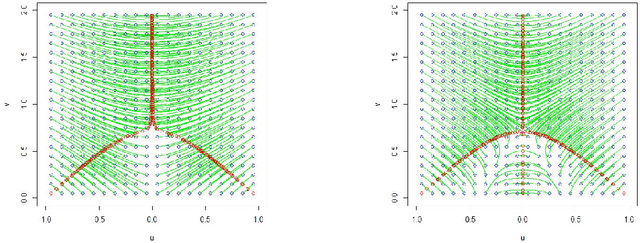
The extraction of filamentary structure from a point cloud is discussed. The filaments are modeled as ridge lines or higher dimensional ridges of an underlying density. We propose two novel algorithms, and provide theoretical guarantees for their convergences. We consider the new algorithms as alternatives to the Subspace Constraint Mean Shift (SCMS) algorithm that do not suffer from a shortcoming of the SCMS that is also revealed in this paper.

Autism Spectrum Disorder Classification using Graph Kernels on Multidimensional Time Series

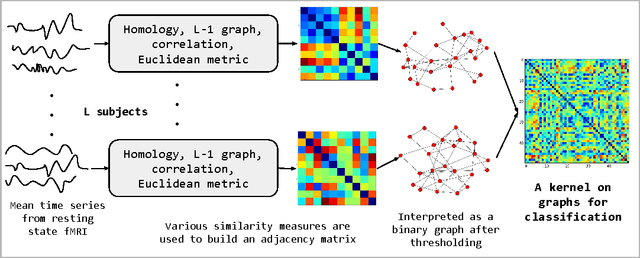
We present an approach to model time series data from resting state fMRI for autism spectrum disorder (ASD) severity classification. We propose to adopt kernel machines and employ graph kernels that define a kernel dot product between two graphs. This enables us to take advantage of spatio-temporal information to capture the dynamics of the brain network, as opposed to aggregating them in the spatial or temporal dimension. In addition to the conventional similarity graphs, we explore the use of L1 graph using sparse coding, and the persistent homology of time delay embeddings, in the proposed pipeline for ASD classification. In our experiments on two datasets from the ABIDE collection, we demonstrate a consistent and significant advantage in using graph kernels over traditional linear or non linear kernels for a variety of time series features.