Graph Max Shift: A Hill-Climbing Method for Graph Clustering

We present a method for graph clustering that is analogous with gradient ascent methods previously proposed for clustering points in space. We show that, when applied to a random geometric graph with data iid from some density with Morse regularity, the method is asymptotically consistent. Here, consistency is understood with respect to a density-level clustering defined by the partition of the support of the density induced by the basins of attraction of the density modes.

Embedding Functional Data: Multidimensional Scaling and Manifold Learning

We adapt concepts, methodology, and theory originally developed in the areas of multidimensional scaling and dimensionality reduction for multivariate data to the functional setting. We focus on classical scaling and Isomap -- prototypical methods that have played important roles in these area -- and showcase their use in the context of functional data analysis. In the process, we highlight the crucial role that the ambient metric plays.

Clustering by Hill-Climbing: Consistency Results

We consider several hill-climbing approaches to clustering as formulated by Fukunaga and Hostetler in the 1970's. We study both continuous-space and discrete-space (i.e., medoid) variants and establish their consistency.

An Asymptotic Equivalence between the Mean-Shift Algorithm and the Cluster Tree

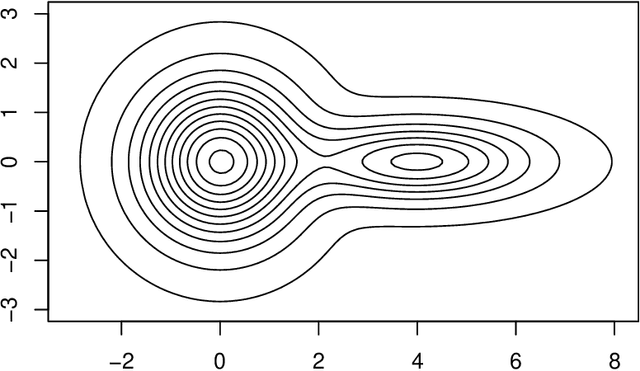
Two important nonparametric approaches to clustering emerged in the 1970's: clustering by level sets or cluster tree as proposed by Hartigan, and clustering by gradient lines or gradient flow as proposed by Fukunaga and Hosteler. In a recent paper, we argue the thesis that these two approaches are fundamentally the same by showing that the gradient flow provides a way to move along the cluster tree. In making a stronger case, we are confronted with the fact the cluster tree does not define a partition of the entire support of the underlying density, while the gradient flow does. In the present paper, we resolve this conundrum by proposing two ways of obtaining a partition from the cluster tree -- each one of them very natural in its own right -- and showing that both of them reduce to the partition given by the gradient flow under standard assumptions on the sampling density.

Level Sets or Gradient Lines? A Unifying View of Modal Clustering

The paper establishes a strong correspondence, if not an equivalence, between two important clustering approaches that emerged in the 1970's: clustering by level sets or cluster tree as proposed by Hartigan and clustering by gradient lines or gradient flow as proposed by Fukunaga and Hosteler.

Algorithms for ridge estimation with convergence guarantees

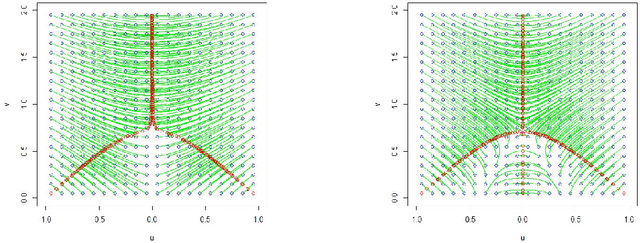
The extraction of filamentary structure from a point cloud is discussed. The filaments are modeled as ridge lines or higher dimensional ridges of an underlying density. We propose two novel algorithms, and provide theoretical guarantees for their convergences. We consider the new algorithms as alternatives to the Subspace Constraint Mean Shift (SCMS) algorithm that do not suffer from a shortcoming of the SCMS that is also revealed in this paper.

Space Partitioning and Regression Mode Seeking via a Mean-Shift-Inspired Algorithm

The mean shift (MS) algorithm is a nonparametric method used to cluster sample points and find the local modes of kernel density estimates, using an idea based on iterative gradient ascent. In this paper we develop a mean-shift-inspired algorithm to estimate the modes of regression functions and partition the sample points in the input space. We prove convergence of the sequences generated by the algorithm and derive the non-asymptotic rates of convergence of the estimated local modes for the underlying regression model. We also demonstrate the utility of the algorithm for data-enabled discovery through an application on biomolecular structure data. An extension to subspace constrained mean shift (SCMS) algorithm used to extract ridges of regression functions is briefly discussed.