Graph Max Shift: A Hill-Climbing Method for Graph Clustering

We present a method for graph clustering that is analogous with gradient ascent methods previously proposed for clustering points in space. We show that, when applied to a random geometric graph with data iid from some density with Morse regularity, the method is asymptotically consistent. Here, consistency is understood with respect to a density-level clustering defined by the partition of the support of the density induced by the basins of attraction of the density modes.

An Axiomatic Definition of Hierarchical Clustering

In this paper, we take an axiomatic approach to defining a population hierarchical clustering for piecewise constant densities, and in a similar manner to Lebesgue integration, extend this definition to more general densities. When the density satisfies some mild conditions, e.g., when it has connected support, is continuous, and vanishes only at infinity, or when the connected components of the density satisfy these conditions, our axiomatic definition results in Hartigan's definition of cluster tree.

Embedding Functional Data: Multidimensional Scaling and Manifold Learning

We adapt concepts, methodology, and theory originally developed in the areas of multidimensional scaling and dimensionality reduction for multivariate data to the functional setting. We focus on classical scaling and Isomap -- prototypical methods that have played important roles in these area -- and showcase their use in the context of functional data analysis. In the process, we highlight the crucial role that the ambient metric plays.

Supervising Embedding Algorithms Using the Stress

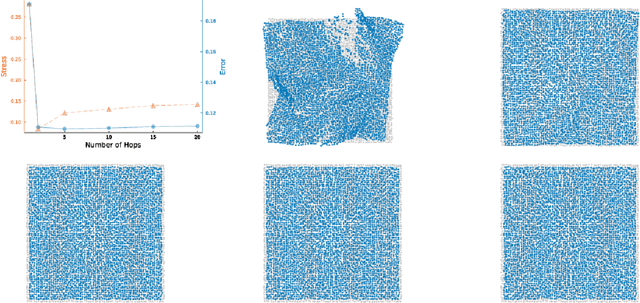
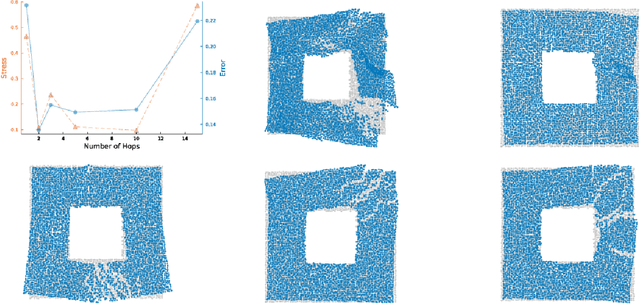
While classical scaling, just like principal component analysis, is parameter-free, most other methods for embedding multivariate data require the selection of one or several parameters. This tuning can be difficult due to the unsupervised nature of the situation. We propose a simple, almost obvious, approach to supervise the choice of tuning parameter(s): minimize a notion of stress. We substantiate this choice by reference to rigidity theory. We extend a result by Aspnes et al. (IEEE Mobile Computing, 2006), showing that general random geometric graphs are trilateration graphs with high probability. And we provide a stability result \`a la Anderson et al. (SIAM Discrete Mathematics, 2010). We illustrate this approach in the context of the MDS-MAP(P) algorithm of Shang and Ruml (IEEE INFOCOM, 2004). As a prototypical patch-stitching method, it requires the choice of patch size, and we use the stress to make that choice data-driven. In this context, we perform a number of experiments to illustrate the validity of using the stress as the basis for tuning parameter selection. In so doing, we uncover a bias-variance tradeoff, which is a phenomenon which may have been overlooked in the multidimensional scaling literature. By turning MDS-MAP(P) into a method for manifold learning, we obtain a local version of Isomap for which the minimization of the stress may also be used for parameter tuning.

Clustering by Hill-Climbing: Consistency Results

We consider several hill-climbing approaches to clustering as formulated by Fukunaga and Hostetler in the 1970's. We study both continuous-space and discrete-space (i.e., medoid) variants and establish their consistency.

An Asymptotic Equivalence between the Mean-Shift Algorithm and the Cluster Tree

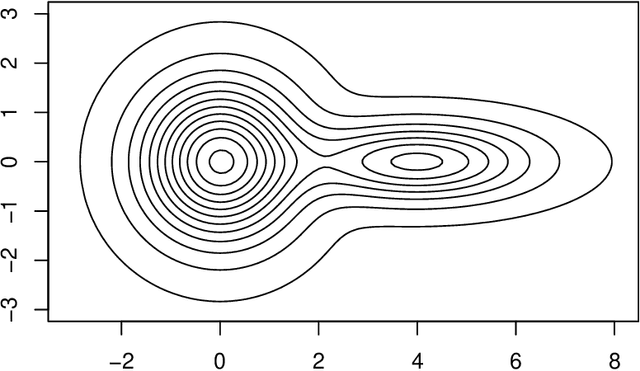
Two important nonparametric approaches to clustering emerged in the 1970's: clustering by level sets or cluster tree as proposed by Hartigan, and clustering by gradient lines or gradient flow as proposed by Fukunaga and Hosteler. In a recent paper, we argue the thesis that these two approaches are fundamentally the same by showing that the gradient flow provides a way to move along the cluster tree. In making a stronger case, we are confronted with the fact the cluster tree does not define a partition of the entire support of the underlying density, while the gradient flow does. In the present paper, we resolve this conundrum by proposing two ways of obtaining a partition from the cluster tree -- each one of them very natural in its own right -- and showing that both of them reduce to the partition given by the gradient flow under standard assumptions on the sampling density.

Level Sets or Gradient Lines? A Unifying View of Modal Clustering

The paper establishes a strong correspondence, if not an equivalence, between two important clustering approaches that emerged in the 1970's: clustering by level sets or cluster tree as proposed by Hartigan and clustering by gradient lines or gradient flow as proposed by Fukunaga and Hosteler.

Minimax Estimation of Distances on a Surface and Minimax Manifold Learning in the Isometric-to-Convex Setting

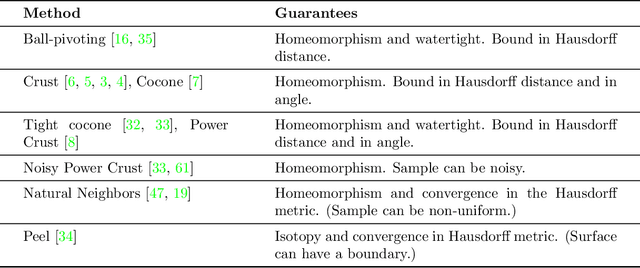
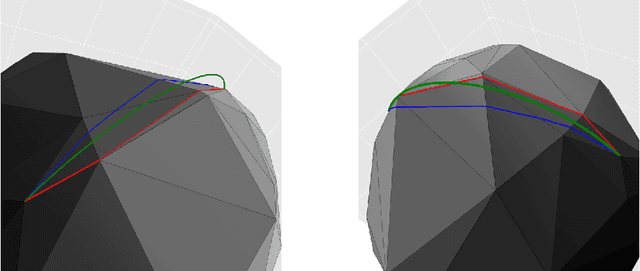
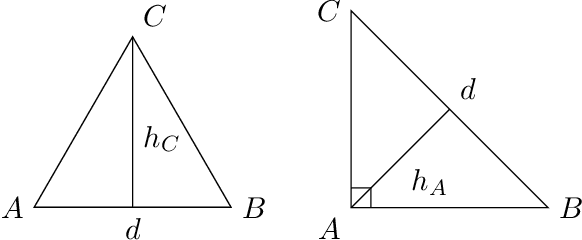
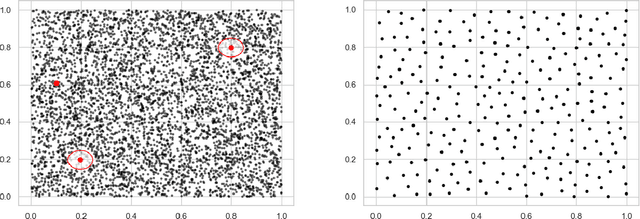
We start by considering the problem of estimating intrinsic distances on a smooth surface. We show that sharper estimates can be obtained via a reconstruction of the surface, and discuss the use of the tangential Delaunay complex for that purpose. We further show that the resulting approximation rate is in fact optimal in an information-theoretic (minimax) sense. We then turn to manifold learning and argue that a variant of Isomap where the distances are instead computed on a reconstructed surface is minimax optimal for the problem of isometric manifold embedding.

Perturbation Bounds for Procrustes, Classical Scaling, and Trilateration, with Applications to Manifold Learning

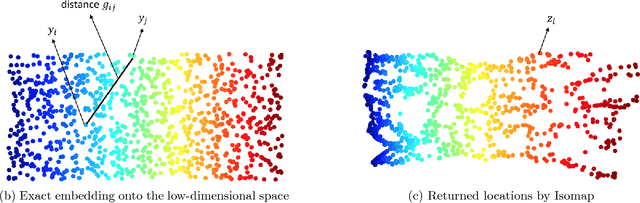
One of the common tasks in unsupervised learning is dimensionality reduction, where the goal is to find meaningful low-dimensional structures hidden in high-dimensional data. Sometimes referred to as manifold learning, this problem is closely related to the problem of localization, which aims at embedding a weighted graph into a low-dimensional Euclidean space. Several methods have been proposed for localization, and also manifold learning. Nonetheless, the robustness property of most of them is little understood. In this paper, we obtain perturbation bounds for classical scaling and trilateration, which are then applied to derive performance bounds for Isomap, Landmark Isomap, and Maximum Variance Unfolding. A new perturbation bound for procrustes analysis plays a key role.

A Simple Approach to Sparse Clustering

Consider the problem of sparse clustering, where it is assumed that only a subset of the features are useful for clustering purposes. In the framework of the COSA method of Friedman and Meulman, subsequently improved in the form of the Sparse K-means method of Witten and Tibshirani, a natural and simpler hill-climbing approach is introduced. The new method is shown to be competitive with these two methods and others.